【磁性体】反磁性、常磁性、強磁性の違いと磁気モーメントの計算問題

磁場 $H$ に存在する互いに相互作用のない磁気モーメント m の向きが，磁場の方向
と平行か反平行しか向けない状況を考える．この場合，それぞれを平行（P）および
反平行（A）状態と呼ぶと，それぞれの状態のエネルギーは次のように書ける．

\begin{cases}E_{p}=-mH \\ E_{A}=mH\end{cases}

問(a) 温度 $T$ において，それぞれの状態をとる確率 $P_P$ および $P_A$ を示せ．ボルツマ
ン定数を $k$ とする．
問(b) 温度 $T$ および磁場 $H$ において平衡状態で観測される磁気モーメント $< m >$
を示せ．
問(c) 単位体積中に磁気モーメントが N 個存在する物質の磁化は
\begin{aligned}M=N <m>\end{aligned}
と書くことができる．高温域$(kT ≫ |mH|)$において，(b) の結果をテイラー展開
することにより，帯磁率$\chi$が温度 $T$ に反比例することを導出せよ．
東北大学材料系院試 2019年材料物性2より引用

磁気モーメントとは
1. 磁気モーメントと電子の運動
2. 補足
反磁性、常磁性、強磁性
ボルツマン分布
1. 補足：本問でボルツマン分布を使用する理由
解答例

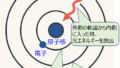
磁気モーメントとは

磁石の強さと向きを示すベクトル量です。磁石は、N極からS極へ磁力線が伸びていますが、その強さと具体的な向きを示しています。

日常生活を送っていると、磁石は何らかの理由で元から磁性を帯びているものだとイメージしますが、実際に物質内部ではどのような現象が起きているのでしょうか。下記で見ていきましょう。

磁気モーメントと電子の運動

物質内部の電子の運動により、磁気モーメントは主に発生します。下記で物理的なイメージを説明します。

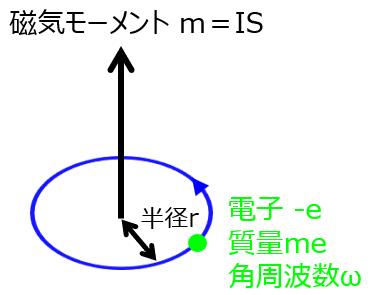
物質中では、電子は原子核の周りで軌道運動をしています。よって、下記のように、質量$m_{e}$の電子$-e$が、半径$r$、角周波数$\omega$で円運動している系を考えます。電流$I$は、1秒間にある面を通過する電荷量のため、周波数$f=\frac{\omega}{2 \pi}$を用いて

\begin{aligned}I=-\dfrac{e \omega}{2 \pi}\end{aligned}

磁気モーメント$|m|$は、環状電流とその閉路の面積の積$|m|=|I|S$であるので

\begin{aligned}|m|&=\dfrac{e \omega}{2 \pi} \pi r^{2} \\ &=\dfrac{e}{2}r^{2} \omega \end{aligned}

で表されます。ちなみに、角運動量$\boldsymbol{L}=|\boldsymbol{r} × \boldsymbol{p}|$は

\begin{aligned}|\boldsymbol{L}|&=|\boldsymbol{r}×\boldsymbol{p}| \\ &=mr^{2}\omega^{2}\end{aligned}

で表されるので、これを(4式)に代入すると

\begin{aligned}\boldsymbol{m}=-\dfrac{e}{2m_{e}}\boldsymbol{L}\end{aligned}

になります。($\boldsymbol{p}$は運動量で$m\boldsymbol{v}$で表されます。)

なお、量子力学の場合、z方向の角運動量$L_{z}=m\hbar$で表されることから

\begin{aligned}m_{z}=-m \mu_{B}\end{aligned}

\begin{aligned}\mu_{B}=\dfrac{e \hbar}{2m_{e}}\end{aligned}

となり、$\mu_{B}$をボーア磁子と言います。

補足

本記事では、固体物理学における磁気モーメントについて取り扱います。電磁気学でも磁気モーメントに関する問題は出題されます。こちらの記事で例題を上げていますので、よろしければご覧ください。

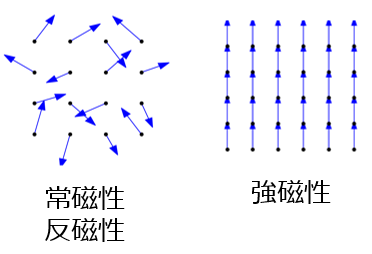
反磁性、常磁性、強磁性

磁性体は、反磁性、常磁性、強磁性を持つものがあります。簡潔に、下記の性質になります。

性質

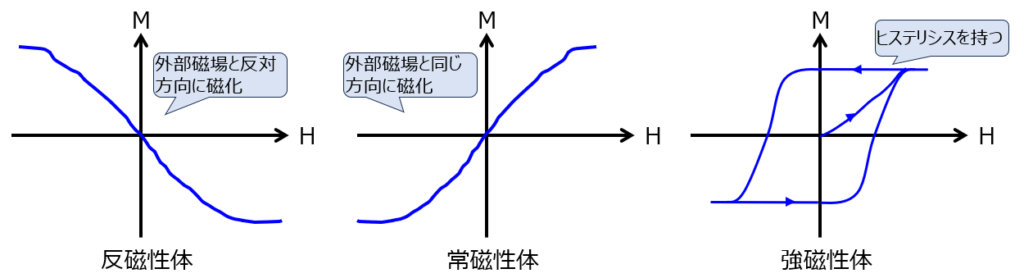
反磁性：磁場をかけた方向と逆向きに磁化すること
常磁性：磁場をかけた方向と同じ向きに磁化すること
強磁性：磁場をかけなくとも、磁化していること

上記の性質から、外部磁場$H$を掛けた時の磁化の強さを見るM-H曲線は下記のようになります。

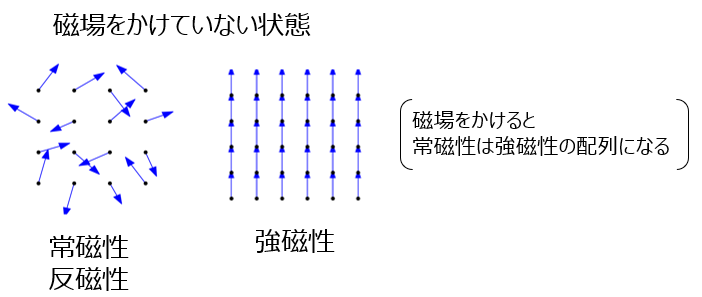
同じく、磁場をかけていない状態での磁気モーメントは下記のようになります。

ボルツマン分布

標記の問題を解くために必要な考え方です。エネルギー準位$E_{i}$の粒子の存在確率$P_{i}$は、分配関数$Z$を用いて

\begin{aligned}E_{i}=\frac{e^{-E_i / (k T)}}{Z}\end{aligned}

で表されます。ここで、分配関数$Z$は、全ての状態のボルツマン因子の和となります。標記の問題では、平行状態と反平行状態の2つしか存在しないので

\begin{aligned}Z = e^{-E_P / (k T)} + e^{-E_A / (k T)}\end{aligned}

となります。$P_Pは$、(9式)の分子を$E_{P}$とし、$P_A$は、$E_{A}$とすれば解けることが分かります。具体的な計算は後段で行います。

補足：本問でボルツマン分布を使用する理由

以前の記事にて、フェルミ・ディラックの分布関数をはじめとする様々な分布関数の性質について説明しました。この中でボルツマン分布についても説明をしました。その時、固体中でボルツマン分布を用いると誤差が大きいとお話ししました。本記事では、固体物理学に関する現象を説明しています。なぜ、使用しているのでしょうか。

明確に説明している文献は見つけられなかったですが。私の認識は下記になります。