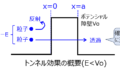
井戸型ポテンシャルとは
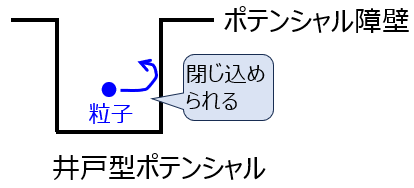
量子力学において、電子が特定のポテンシャル領域に閉じ込められている状況をモデル化したものになります。
メーカーでのデバイス設計など、様々な工学分野で応用される考え方で、工学部の院試でも頻出分野になります。理学部の院試では、スピン演算子や散乱問題が出題されることもありますが、工学部については8,9割方ポテンシャル問題が出てきます。
このように、学生時代の勉強や社会に出てから仕事をしていく上で大変重要な分野になります。本記事では、試験で問われがちなことをまとめます。理解の助けになれば幸いです。
シュレーディンガー方程式
ある系における量子の分布を示す関係式です。量子の質量を\(m\)、プランク定数\(h\)に\(2\pi\)を除したものを\(\hbar\)、ある地点\(\boldsymbol{r}\)のポテンシャル障壁を\(V(\boldsymbol{r})\)、波動関数を\(\Psi\)とすると、時間依存型は下記で表されます。
\begin{aligned}
\left\lbrack -\frac{\hbar^2}{2m} \nabla^2 + V(\mathbf{r}, t) \right\rbrack \Psi(\mathbf{r}, t)=i\hbar \frac{\partial \Psi(\mathbf{r}, t)}{\partial t} \end{aligned}
ポテンシャル問題を解く場合は、定常状態を考えることが多いです。\(\Psi(\boldsymbol{r},t)=\psi(x)e^{-i \omega t}\)とすると、上式は
\begin{aligned}\left\lbrack -\frac{\hbar^2}{2m} \nabla^2 + V(\mathbf{r}, t) \right\rbrack \phi(\boldsymbol{r})e^{-i \omega t}=\hbar \omega \psi(\boldsymbol{r})e^{-i \omega t}\end{aligned}
時間項を削除し、\(E=\hbar \omega\)と置くと下記の形になります。
\begin{aligned}\left\lbrack -\frac{\hbar^2}{2m} \nabla^2 + V(\mathbf{r}) \right\rbrack \psi(\mathbf{r}) = E \psi(\mathbf{r})\end{aligned}
定常型の方程式で、院試の前半の設問でよく用います。
波動関数
ある系における量子の存在確率を考えるために導入する関数です。波動関数そのものを観測することはできませんが、2乗すると、量子がその場所に存在する確率密度\(P(\boldsymbol{r},t)\)になります。
\begin{aligned}P(\boldsymbol{r},t)=|\Psi(\boldsymbol{r},t)|^{2}\end{aligned}
確率密度を表すため、波動関数の2乗を系の存在する領域全域で積分する場合、結果は1(確率100%)になります。(この考え方、試験でよく使うので覚えましょう。規格化条件とも言います。)
\begin{aligned}\int^{\infty}_{-\infty}|\Psi(\boldsymbol{r},t)|^{2}d\boldsymbol{r}=1\end{aligned}
波動関数を導入する理由
量子力学では、状態を確率的に表現する必要があるためです。古典力学では、粒子の位置と運動量が正確に決定できますが、量子力学ではハイゼンベルグの不確定性原理により出来ないからです。
過去の記事により、不確定性原理は下記の式で表されます。
\begin{aligned}\Delta x \Delta p=\dfrac{\hbar}{2}\end{aligned}
\(\Delta x,\Delta p\)は、それぞれ位置と運動量の不確かさです。位置の不正確さ\(\Delta x\)を小さくしようとすると、測定範囲を狭める必要があります。しかし、狭い計測範囲の場合、計測した粒子の運動状態を正確に測ることができないため、\(\Delta p\)は大きくなってしまいます。
このように、\(\Delta x\)と\(\Delta p\)はトレードオフの関係になります。一つの粒子に対し二つの状態を正確に計算できないため、確率として統計的に表現するわけですね。
井戸型ポテンシャルにおける波動関数
無限井戸型ポテンシャル(0<x<a)の場合
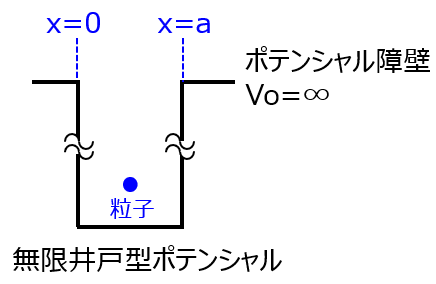
まず、無限大の障壁ポテンシャル\(0<x<a\)からなる井戸型ポテンシャルの粒子の分布(定常状態)を考えます。
分布を調べるには波動関数を求めると良いです。\(0<x<a\)以外の領域は、無限ポテンシャルですので\(\psi(x)=0\)です。一方で、井戸の底の領域\(0<x<a\)における波動関数は、定常状態のシュレーディンガー方程式(3)式を変形し
\begin{aligned}\dfrac{d^{2} \psi}{dx^{2}}=-\dfrac{2mE}{\hbar^{2}}\psi\end{aligned}
\(\phi(x)=e^{ax}\)を仮定すると、上式の解は
\begin{aligned}\psi=A\sin\left(\dfrac{\sqrt{2mE}}{\hbar}\right)+B\cos\left(\dfrac{\sqrt{2mE}}{\hbar}\right)\end{aligned}
ここに\(x=0,a\)で波動関数\(\psi=0\)になる境界条件を適用すると、\(B=0\)が得られる。よって、求める(0<x<a)での波動関数は
\begin{cases}\psi(x)=A\sin\left(\dfrac{\sqrt{2mE}}{\hbar}\right)x \\ \dfrac{\sqrt{2mE}}{\hbar}a=n \pi \end{cases}
ここで、\(n\)は自然数とする。最後に、規格化条件(4)式を適用し
\begin{aligned}\int^{a}_{0}A^{2}\sin^{2}\left(\dfrac{\sqrt{2mE}}{\hbar}\right)x dx =1\end{aligned}
\begin{aligned}A^{2}\dfrac{a}{2} =1\end{aligned}
\(A=\sqrt{\dfrac{2}{a}}\)が得られるので
\begin{aligned}\psi=\sqrt{\dfrac{2}{a}}\sin\dfrac{n\pi}{a}x\end{aligned}
エネルギー固有値
前節の(9)式の第2式にエネルギー\(E\)項が含まれています。これを整理すると
\begin{aligned}E_{n}=\dfrac{x \hbar^{2} \pi}{2 m a^{2}}\end{aligned}
が得られます。自然数\(n\)が項に含まれているため、無限井戸型ポテンシャルの底に存在する粒子は離散的なエネルギー状態を取ることが分かりました。
無限井戸型ポテンシャル(-a<x<a)の場合
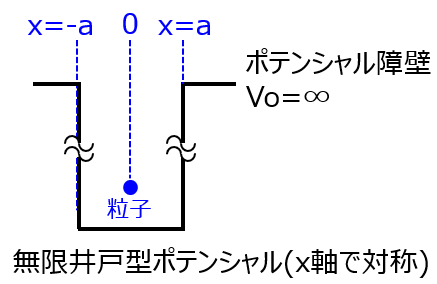
問題によっては、障壁ポテンシャルが負の領域まで延び、対称になっている場合も出題されます。この時の(-a<x<a)の波動関数は(8)式に対し、境界条件\(x=±a\)を考えれば良く、自然数\(n\)の偶奇によって下記に分かれます。
\begin{aligned}\psi(x)=\begin{cases}A \sin\left(\dfrac{\sqrt{2mE}}{\hbar}\right)x \quad (n:偶数) \\ B \cos\left(\dfrac{\sqrt{2mE}}{\hbar}\right)x \quad (n:奇数) \end{cases} \end{aligned}
ただし、\(\dfrac{\sqrt{2mE}}{\hbar}a=\dfrac{\pi}{2}n\)です。
同じく、規格化条件を考える。
\begin{aligned}\int^{a}_{-a}A^{2}\sin^{2}\left(\dfrac{\pi n}{2a}\right) =1\end{aligned}
より、\(A=\sqrt{\dfrac{1}{a}}\)。求める波動関数は
\begin{aligned}\psi(x)=\begin{cases}\sqrt{\dfrac{1}{a}} \sin\left(\dfrac{\sqrt{2mE}}{\hbar}\right)x \quad (n:偶数) \\ \sqrt{\dfrac{1}{a}} \cos\left(\dfrac{\sqrt{2mE}}{\hbar}\right)x \quad (n:奇数) \end{cases} \end{aligned}
エネルギー固有値は
\begin{aligned}E_{n}=\dfrac{x \hbar^{2} \pi}{8 m a^{2}}\end{aligned}
系の取り得る基底エネルギーは、井戸の幅\(a\)に依存し、\(a\)小さいほど大きくなることが分かりました。
有限ポテンシャルの場合
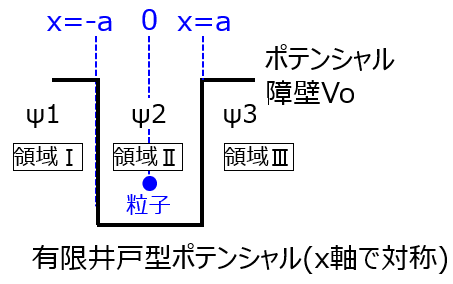
非常に計算が長く、試験でも何かしらの簡略化、誘導が前提で出題されます。本記事では概要の説明をします。
例として、\(|x|>a\)はポテンシャル障壁\(V_{o}\)、他の領域では変わらず\(V_{o}=0\)の有限井戸型ポテンシャルを考えます。
それぞれの領域のシュレーディンガー方程式は
\begin{cases}\dfrac{d^{2} \psi}{dx^{2}}=\dfrac{2m(V_{o}-E)}{\hbar^{2}}\psi \quad (|x|>a) \\ \dfrac{d^{2} \psi}{dx^{2}}=-\dfrac{2mE}{\hbar^{2}}\psi \quad (|x|<a)\end{cases}
\(x<-a,-a<x<a,x>a\)それぞれの領域の波動関数を\(\psi_{1},\psi_{2},\psi_{3}\)とすると
\begin{cases}\psi_{1}=Ce^\left(\frac{\sqrt{2m(V_{o}-E)}}{\hbar}x\right)+C_{1}e^\left(-\frac{\sqrt{2m(V_{o}-E)}}{\hbar}x\right) \\ \psi_{2}=A\sin\left(\frac{\sqrt{2mE}}{\hbar}x\right)+B\cos\left(\frac{\sqrt{2mE}}{\hbar}x\right) \\ \psi_{3}=De^\left(-\frac{\sqrt{2m(V_{o}-E)}}{\hbar}x\right)+D_{1}e^\left(\frac{\sqrt{2m(V_{o}-E)}}{\hbar}x\right)\end{cases}
\(x→\infty\)の極限を考えると波動関数\(\psi_{1},\psi_{3}→0\)になるので、\(C_{1}=D_{1}=0\)
\(x=-a,a\)で波動関数は連続なので、\(\psi_{1}=\psi_{2},\psi_{1}^{\prime}=\psi_{2}^{\prime},\psi_{2}=\psi_{3},\psi_{2}^{\prime}=\psi_{3}^{\prime}\)、\(\alpha=\frac{\sqrt{2mE}}{\hbar},\beta=\frac{\sqrt{2m(V_{o}-E)}}{\hbar}\)とし
\begin{cases}-A\sin \alpha a+B \cos \alpha a=Ce^{-\beta a} \\ \alpha A\cos \alpha a+ \alpha B\sin \alpha a=\beta C e^{-\beta a} \\ A\sin \alpha a+B\cos \alpha a=De^{-\beta a} \\ \alpha A \cos \alpha a-\alpha B \sin \alpha a=-\beta De^{-\beta a}\end{cases}
上式を整理すると、下記の2組4式が得られる。
\begin{cases}2A\sin \alpha a=(D-C)e^{-\beta a} \\ 2 \alpha A \cos \alpha a=-\beta(D-C)e^{-\beta a}\end{cases}
\begin{cases}2B\cos \alpha a=(C+D)e^{-\beta a} \\ 2 \alpha B \cos \alpha a=-\beta(C+D)e^{-\beta a}\end{cases}
無限井戸型ポテンシャルと同様に、\(A≠0\)または\(B≠0\)の場合を考える。
(i)\(A≠0\)のとき、(21)式から\(D≠C\)、第二式に第一式を割って
\begin{aligned}\alpha \dfrac{\cos \alpha a}{\sin \alpha a}=-\beta\end{aligned}
(ii)\(B≠0\)のとき、(22)式から同様にして
\begin{aligned}\alpha\dfrac{\sin \alpha a}{\cos \alpha a}=\beta\end{aligned}
\(A≠0\)かつ\(B≠0\)のとき、\(\tan \alpha a=-1\)だが、負の値は取れないため不適
結局、\(A=0,B≠0\)、\(A≠0,B=0\)の2通りある。それぞれの場合で、\(C=D,C=-D\)になる。\(\alpha a= \xi ,\beta a=\eta\)とすると、下記のようになる。
\begin{cases}\xi \tan \xi=\eta \\ \xi \dfrac{\cos \xi}{\sin \xi}=\xi \cot \xi=-\eta\end{cases}
\begin{aligned}\xi^{2}+\eta^{2}=\frac{2mV_{o}a^{2}}{\hbar^{2}}\end{aligned}
$\xi,\eta$の具体的な値を計算で求めることはできないが、(25)式、(26)式をグラフ化し、おおよその値を考えることができる。(グラフの交点)
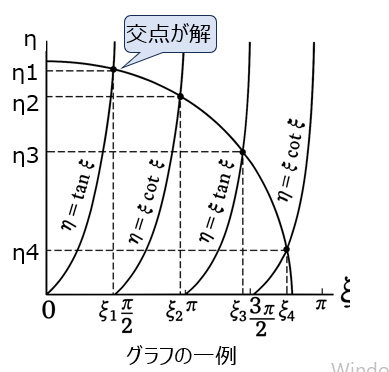
最後に
シュレーディンガー方程式の波動関数の解の仮定方法は問題ごとに異なる場合があります。例えば、本記事では\(e^{ax}\)とexp項内部に虚数は考えずに解きましたが、虚数有りとして解くよう誘導している場合もあります。
ただ、結局は仮定した解をシュレーディンガー方程式に代入し、境界条件を用いて求めることに変わりないです。落ち着いて計算していきましょう。