(1)図1のように、半径\(a,b,c\)の導体球1,2,3を相互の距離\(r_{ab},r_{ac},r_{bc}\)となるように配置する。各導体間の電位係数\(p_{11},p_{12},p_{13},p_{21},p_{22},p_{23},p_{31},p_{32},p_{33}\)を求めよ。但し、球の半径は導体間の距離に対し、十分小さいと仮定する。
(2)図2のように、同じ形状を持った導体1,3を導体2の内外にそれぞれ配置する。導体1と導体3の相互作用を無くするためには、導体2を接地することが有効であることを証明せよ。(静電遮蔽)
なお、証明には導体1~3の電荷、電位\(Q_{1},Q_{2},Q_{3},V_{1},V_{2},V_{3}\)、および容量係数\(q_{11},q_{12}, \cdots ,q_{33}\)を用いて良い。
電位係数、容量係数の説明
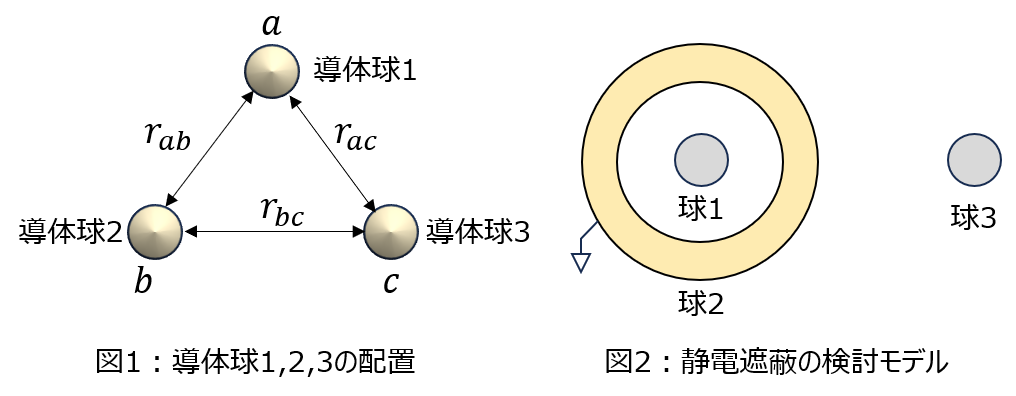
電位係数とは
導体間の電位の相互作用を表しています。
例えば、n個の導体があり、そのうちの1番目の導体に電荷\(Q_{1}\)を与えたとします。(他の導体2~n)の電荷は0。)
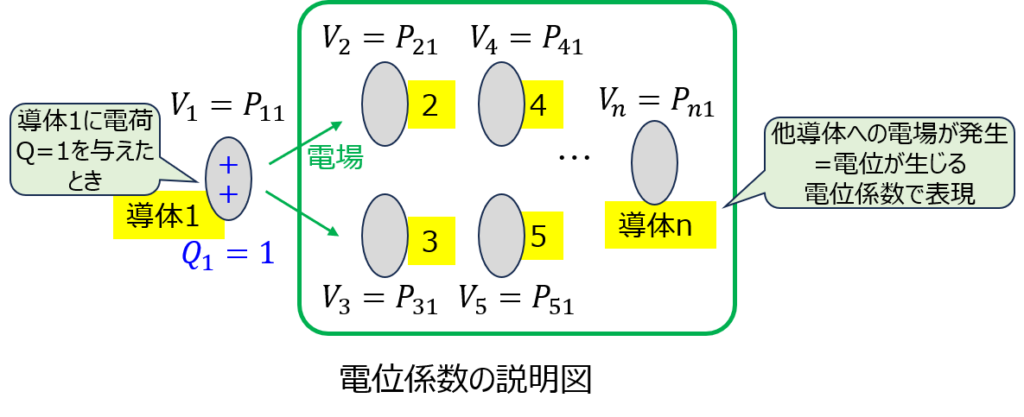
このとき、導体1から発生する電場により導体nで発生する電位を\(p_{n1}\)とし、これを電位係数と呼びます。
導体1と2、導体1と3など、他の組み合わせに対しても同じことが言えますので、下記のように行列表示ができます。
\begin{aligned}\begin{pmatrix} \phi _{1} \\ \phi _{2} \\ \vdots \\ \phi _{n} \end{pmatrix}=\begin{pmatrix} p_{11}p_{12} & \ldots p_{1n} \\ p_{21}p_{22} & \ldots p _{2n} \\ \vdots \vdots & \vdots \\ p_{n1} p_{n2} & \ldots p_{nn} \end{pmatrix}\begin{pmatrix} Q _{1} \\ Q _{2} \\ \vdots \\ Q _{n} \end{pmatrix}\end{aligned}
左辺の\(V_{1},V_{2}, \cdots , V_{n}\)は、導体1~nに電荷\(Q_{1},Q_{2}, \cdots , Q_{n}\)を与えた時の各導体の電位(合計値)になります。
電位係数の性質
下記を覚えておくと、試験中に答案確認ができる材料になります。
異なる導体k、導体lにおいて
- \(p_{kl}=p_{lk}>0\)
- \(p_{kk}>p_{kl}\)
意味として、
- 正の電荷を与えたとき、電位は負にならないこと。
- 電荷を与えた導体自身の電位は、他の導体における電位より大きい。(物理的な距離から)
ことを指しています。
容量係数(誘導係数)の説明
(1)式を逆行列を利用して解くと
\begin{aligned}\begin{pmatrix} Q _{1} \\ Q _{2} \\ \vdots \\ Q _{n} \end{pmatrix}=\begin{pmatrix} C_{11}C_{12} & \ldots C_{1n} \\ C_{21}C_{22} & \ldots C _{2n} \\ \vdots \vdots & \vdots \\ C_{n1} C_{n2} & \ldots C_{nn} \end{pmatrix}\begin{pmatrix} \phi _{1} \\ \phi _{2} \\ \vdots \\ \phi _{n} \end{pmatrix}\end{aligned}
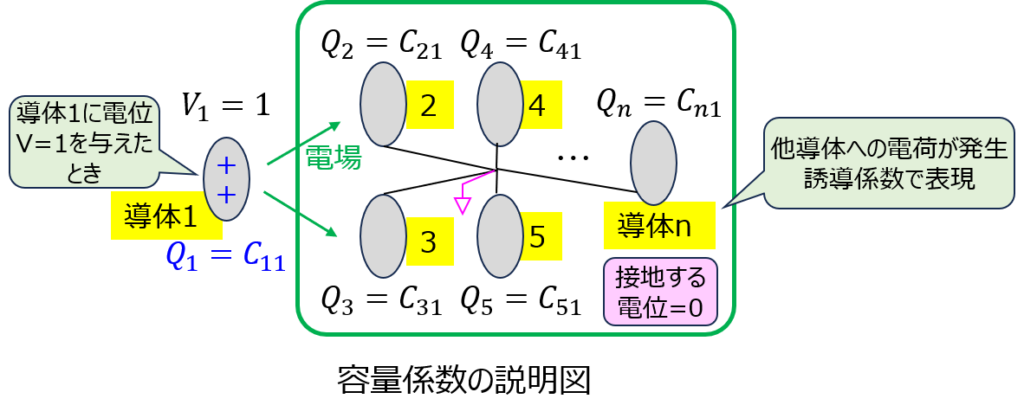
になります。導体1に電位\(V_{1}\)を与えた時、導体nに誘起する電荷量を\(q_{n1}\)と表記し、誘導係数と呼びます。
また、\(q_{11},q_{22},\cdots ,q_{nn}\)など、添え字同士が共通の場合を容量係数と呼びます。
先ほど同じく、左辺の\(Q_{1},Q_{2}, \cdots , Q_{n}\)は、導体1~nに電位\(V_{1},V_{2}, \cdots , V_{n}\)を与えた時の各導体の電位(合計値)になります。
容量係数/誘導係数の性質
いくつか、電位係数と異なる点があります。
異なる導体k、導体lにおいて
- \(q_{kl}=q_{lk}<0\)
- \(q_{kk}>0\)
- \(\sum^{n}_{k=1}q_{kl} ≧0\)
対称性に関しては電位係数と同じことが言えます。
注意したい事項として、\(k ≠ l\)の電位係数\(q_{kl}\)は負になることです。これは、ある導体kに正の電荷\(Q_{k}\)を与えたとき、他の導体に対しては電場を受ける側になり、負の電荷が誘起するためです。
また、\(q_{kk}\)は導体k自体の静電容量\(C\)を表しています。問題によっては、静電容量を求めてから容量係数/誘導係数の議論に入ることがあります。
解答例
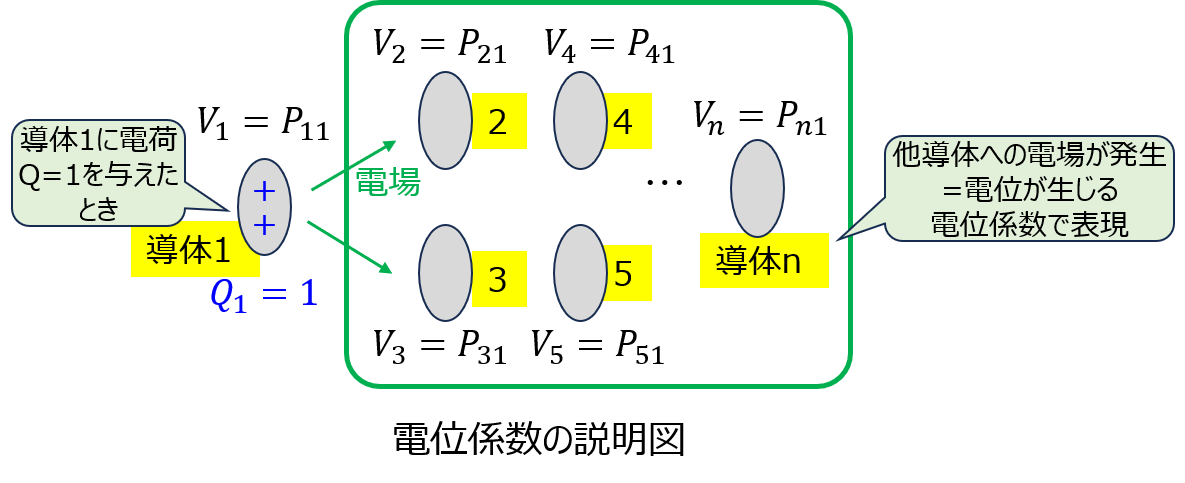
(1)3つの導体球における電位係数
各導体に電荷\(Q_{1},Q_{2},Q_{3}\)を与えたときの各導体の電位\(V_{1},V_{2},V_{3}\)を考える。導体間の距離に対し、導体球の大きさは無視できる。クーロンの法則により
\begin{cases}V_{1}=\dfrac{1}{4 \pi \varepsilon_{o}}\left ( \dfrac{Q_{1}}{a}+\dfrac{Q_{2}}{r_{ab}}+\dfrac{Q_{3}}{r_{ac}} \right ) \\ V_{2}=\dfrac{1}{4 \pi \varepsilon_{o}} \left( \dfrac{Q_{1}}{r_{ab}}+\dfrac{Q_{2}}{b}+\dfrac{Q_{3}}{r_{bc}} \right ) \\ V_{3}=\dfrac{1}{4 \pi \varepsilon_{o}} \left( \dfrac{Q_{1}}{r_{ab}}+\dfrac{Q_{2}}{r_{bc}}+\dfrac{Q_{3}}{c} \right) \end{cases}
これを電位係数の(1)式と比較して
\begin{cases}p_{11}=\dfrac{1}{4 \pi \varepsilon_{o}a} \\ p_{12}=p_{21}=\dfrac{1}{4 \pi \varepsilon_{o} r_{ab}} \\ p_{13}=p_{31}=\dfrac{1}{4 \pi \varepsilon_{o} r_{ac}} \\ p_{22}=\dfrac{1}{ 4 \pi \varepsilon_{o} b} \\ p_{23}=p_{32}=\dfrac{1}{4 \pi \varepsilon_{o} r_{bc}} \\ p_{33}=\dfrac{1}{ 4 \pi \varepsilon_{o} c}\end{cases}
(2)静電遮蔽の証明
方針
導体1と3の容量係数の式
\begin{aligned}Q_{1}=q_{11}V_{1}+q_{12}V_{2}+q_{13}V_{3} \\Q_{3}=q_{31}V_{1}+q_{32}V_{2}+q_{33}V_{3}\end{aligned}
について、\(Q_{1}=q_{11}V_{1},Q_{3}=q_{33}V_{3}\)形にすることがゴールです。
この場合、導体1,3の電荷、電位は自身の特性にのみ影響し、他の導体の影響が無いと言えるからです。
証明
まず、導体1に電荷を与えず、\(Q_{1}\)の場合を考える。導体1,2の間で電場は発生しないので、\(V_{1}=V_{2}\)になる。
これを、\(Q_{1}=q_{11}V_{1}+q_{12}V_{2}+q_{13}V_{3}\)に代入すると
\begin{aligned}0=(q_{11}+q_{21})V_{2}+q_{31}V_{3}\end{aligned}
を得る。\(V_{2},V_{3}\)の値に依らず、上式は成立するので
\begin{cases}q_{11}=-q_{21} \\ q_{31}=0\end{cases}
の必要がある。この関係を(4)式に代入すると
\begin{aligned}Q_{1}=q_{11}(V_{1}-V_{2})\end{aligned}
を得られる。導体2を接地した時\(V_{2}\)となるので上式は\(Q_{1}=q_{11}V_{1}\)となる。
よって、導体1で発生する電荷、電位は自身の特性にのみ依存する。・・・(i)
一方で、導体3についても考える。\(q_{13}=q_{31}=0\)で、導体2は接地していることから、同じく\(V_{2}=0\)
よって、\(Q_{3}=q_{33}V_{3}\)を導くことができ、他の導体の影響を受けない。・・・(ii)
(i),(ii)より、題意は示された。
最後に
電位係数を用いる問題は、院試で出題されることは少ないものの、出て来た時には凄く差が付きやすい分野になります。
本記事で取り上げたような基本的な問題については解けるようにしておきましょう。