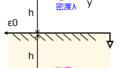
下記5つの系において、働く力を答えよ。特に(1)~(3)は仮想変位を用いよ。
(1)電荷量Q(一定)、面積S、極板間の長さdの平板コンデンサの一方の極板に外力を加え\(\Delta d\)動かしたときの力の量。(図1)
(2)電位差V(一定)、一辺の長さがa、極板間の長さdの正方形コンデンサに、誘電体を長さx分挿入している。さらに\(\Delta x\)挿入するときに発生する力。(図2)
(3)誘電率\(\varepsilon_{1},\varepsilon_{2}\)の誘電体の境界面に作用する力。(電界が境界面に対し垂直のとき)(図3)
(4)電荷量Q(一定)、一辺の長さが\(a\)の正方形コンデンサの極板全体にかかる力。極板間の距離は\(d\)とし、誘電体\(\varepsilon_{1},\varepsilon_{2}\)が、長さ\(t,a-t\)でそれぞれ挿入されているとする。(図4)
(5)透磁率\(\mu_{1},\mu_{2}\)の磁性体の境界面に作用する力。(磁界が境界面に対し垂直のとき)(図5)
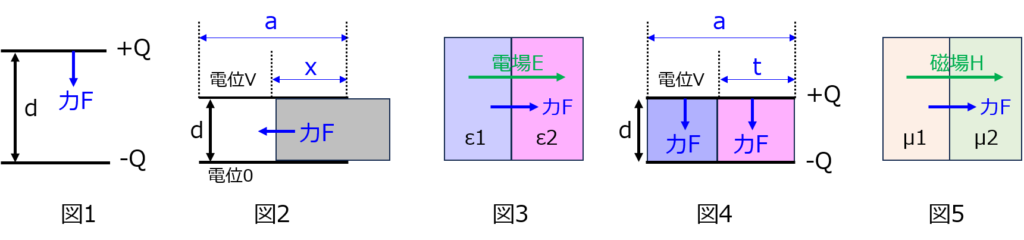
仮想変位とは
ある系において、物質をほんの少し\(\Delta x\)移動させることを言います。このときに発生するエネルギーの微小変化を利用し、どの程度の力が瞬間的にかかったのかを考えます。
微小の変位を考える理由として、力のかかり方が変化前と変化後で一定とみなすことができるからです。だから、変化前の力を考えることができます。
もし、一定以上の量を移動させたときは、位置の変化による影響で、変化前後でかかる力が変わる可能性があります。このようなリスクを排除するため、仮想変位では微小変化量で議論しているわけですね。
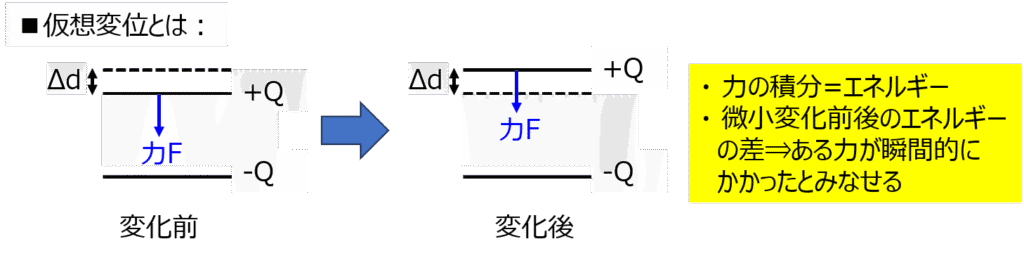
仮想変位を利用した力の求め方
- 微小変化\(\Delta x\)前後で、それぞれの系が保有するエネルギー\(U_{1},U_{2}\)を求める。
- \(F \Delta x=U_{2}-U_{1}\)を解き、外力\(F\)を求める。
力の積分はエネルギーになるため、上記の関係が成立します。大学受験(高校物理)でも同じ計算をしたことがあるかもしれません。
また、大学物理である今、エネルギー\(U_{1}\)を位置で微分する方法でも求めることができます。豊富な例題を用いて、それぞれ考えています。
解答例
(1)一方の極板に外力を加え\(\Delta d\)動かしたときの力
仮想変位
変化前のコンデンサの静電容量\(C_{1}\)、静電エネルギー\(U_{1}\)は
\begin{cases}C_{1}=\dfrac{\varepsilon_{o}S}{d} \\ U_{1}=\dfrac{Q^{2}}{2C_{1}}=\dfrac{Q^{2}}{2\varepsilon_{o}S}d\end{cases}
変化後のコンデンサの静電容量\(C_{2}\)、静電エネルギー\(U_{2}\)は
\begin{cases}C_{2}=\dfrac{\varepsilon_{o}S}{d+\Delta d} \\ U_{2}=\dfrac{Q^{2}}{2C_{2}}=\dfrac{Q^{2}}{2\varepsilon_{o}S}(d+ \Delta d)\end{cases}
微小変位のため、外力の大きさは一定であるとみなせるため
\begin{aligned}F \Delta d=U_{2}-U_{1} \\ F=\dfrac{Q^{2}}{2 \varepsilon_{o}S}\end{aligned}
微分を用いた方法
(1)式より、静電エネルギ\(U_{1}\)について、極板間の長さ\(d\)が変数に相当する。これを\(d\)で微分することで
\begin{aligned}F=\dfrac{\partial U_{1}}{\partial d}=\dfrac{Q^{2}}{2 \varepsilon_{o}S}\end{aligned}
(2)誘電体を挿入するときに引き込まれる力
仮想変位
外力を加える前の静電容量\(C_{1}\)、静電エネルギー\(U_{1}\)は
\begin{cases}C_{1}=\dfrac{l+(\varepsilon_{r}-1)x}{l}C_{o} \\ U_{1}=\dfrac{l+(\varepsilon_{r}-1)x}{2l}C_{o}V^{2}\end{cases}
外力を加えた後の静電容量\(C_{2}\)、静電エネルギー\(U_{2}\)は
\begin{cases}C_{2}=\dfrac{l+(\varepsilon_{r}-1)(x+ \Delta x)}{l}C_{o} \\ U_{2}=\dfrac{l+(\varepsilon_{r}-1)(x+\Delta x)}{2l}C_{o}V^{2}\end{cases}
以上より、求める外力の大きさは
\begin{aligned}F=(U_{2}-U_{1})/\Delta d = \dfrac{l+(\varepsilon_{r}-1)\Delta x}{2l}C_{o}V^{2}\end{aligned}
微分を用いた方法
(5)式より、xが変数なので
\begin{aligned}F=\dfrac{\partial U_{1}}{\partial x}=\dfrac{l+(\varepsilon_{r}-1)}{2l}C_{o}V^{2}\end{aligned}
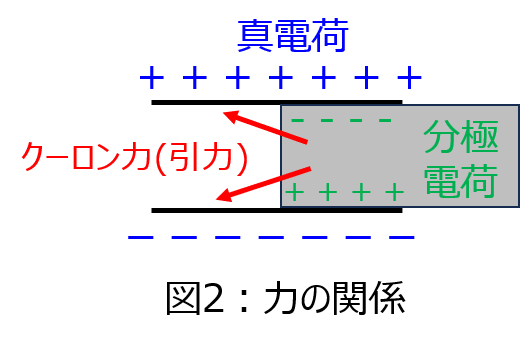
補足
図や結果から分かるように、誘電体には引力が働いています。これは、極板の電荷に対し、誘電体で発生する分極電荷の符号が逆であるため、引き合う力でクーロン力が働くためです。
(3)誘電体の境界面に作用する力
電束密度\(D\)は二つの媒質間で等しい。
媒質1の電場を\(E_{1}\)、媒質2の電場を\(E_{2}\)とする。仮想変位により、\(\Delta x\)を媒質1から2へ変位させたとすると、その部分の静電エネルギーの変化は
\begin{aligned}\Delta U&=\dfrac{E_{1}D}{2}\Delta x – \dfrac{E_{2}D}{2}\Delta x \\ &=\dfrac{D^{2}}{2}\left ( \dfrac{1}{\varepsilon_{2}}-\dfrac{1}{\varepsilon_{2}} \right )\Delta x\end{aligned}
以上より、求める力は
\begin{aligned}&F \Delta x=-\Delta U \\ &F=\dfrac{D^{2}}{2}\left ( \dfrac{1}{\varepsilon_{2}}-\dfrac{1}{\varepsilon_{2}} \right )\end{aligned}
(4)電場が平行に作用する場合の極板に働く力
微分を用いて解を導きます。
与えられたコンデンサの静電容量\(C\)を考える。誘電体1、誘電体2の並列接続と考えられるので
\begin{aligned}C=\dfrac{\varepsilon_{1}at}{d}+\dfrac{\varepsilon_{2}a(a-t)}{d}\end{aligned}
静電エネルギー\(U\)は
\begin{aligned}U&=\dfrac{Q^{2}}{2C} \\ &=\dfrac{Q^{2}d}{2\varepsilon_{1}at+\varepsilon_{2}a(a-t)}\end{aligned}
dが変数なので、求める力は
\begin{aligned}F&=\dfrac{\partial U}{\partial d} \\ &=\dfrac{Q^{2}}{2C} \\ &=\dfrac{Q^{2}}{2\varepsilon_{1}at+\varepsilon_{2}a(a-t)}\end{aligned}
(5)磁性体の境界面に作用する力
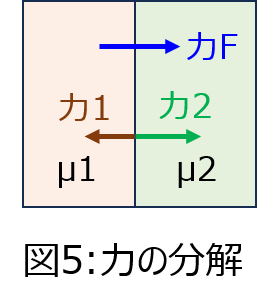
本問は参考程度です。力のかかり方としては収縮力になっているため、誘電体の場合と向きが逆になります。(マクスウェルの応力が関係しています。)
磁性体1にかかる力\(F_{1}\)は
\begin{aligned}F_{1}=\dfrac{H_{1}B}{2}=\dfrac{B^{2}}{2\mu_{1}}\end{aligned}
同じく、磁性体2にかかる力\(F_{2}\)は
\begin{aligned}F_{2}=\dfrac{H_{2}B}{2}=\dfrac{B^{2}}{2\mu_{2}}\end{aligned}
これより、求める力\(F=F_{2}-F_{1}\)は
\begin{aligned}F=\dfrac{B^{2}}{2} \left( \dfrac{1}{\mu_{2}} – \dfrac{1}{\mu_{1}} \right)\end{aligned}