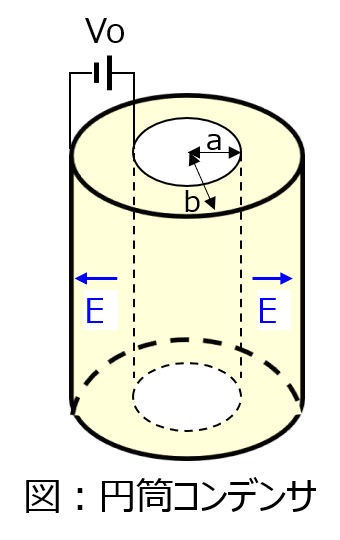
下記の図のように、内径\(a\)、外径\(b\)の円筒コンデンサが存在する。内径の電位は\(V(a)=V_{o}\)、外径の電位は\(V_{b}=0\)とする。この時、電位\(V(r)(a<r<b)\)をラプラス方程式\(\Delta V(r)=0\)を上記の境界条件を解くことにより求めよ。また、この結果を用いて電場\(E(r)\)も求めよ。
なお、下記の式を用いて良い。
\begin{aligned}\Delta \phi=\dfrac{1}{r}\dfrac{\partial}{\partial r}\left(r \dfrac{\partial V}{\partial r} \right)+\dfrac{1}{r^{2}}\dfrac{\partial ^{2}V}{\partial \phi^{2}}+\dfrac{\partial^{2} V}{\partial z^{2}}\end{aligned}
\begin{aligned}\nabla \phi=\dfrac{\partial V}{\partial r}\boldsymbol{\widehat{r}}+\dfrac{1}{r}\dfrac{\partial V}{\partial \phi}\boldsymbol{\widehat{\phi}}+\dfrac{\partial \phi}{\partial z}\boldsymbol{\widehat{z}}\end{aligned}
ラプラス方程式とは
電位の空間的な分布と電荷の分布の関係を表す方程式を言います。(具体的な式の内容は下記で導出しています。)
特に、ある閉曲面において電荷が実際に存在している場合は、ポアソン方程式と呼ばれます。逆に、電荷が存在しない場合はラプラス方程式と言います。本問では後者を例として取り上げます。
両者の呼び名は異なれど、導出自体は同じ手順で出来ます。あくまでも、私たちが試しに取った空間領域のうち、電荷の存在有無によって方程式の名前が変わるだけで、物理的意味、計算内容は変わりません。
ラプラス方程式の導出
マクスウェル方程式のうち、ガウスの法則\(\nabla ・ \boldsymbol{E}=\varepsilon_{o}/\rho\)を起点に考えます。\(\boldsymbol{E}=-\nabla V\)を代入すると
\begin{aligned}\Delta V=-\dfrac{\rho}{\varepsilon_{o}}\end{aligned}
が得られます。これがポアソン方程式を指します。
一方で、右辺\(\rho=0\)のときは(右辺)=0となり、ラプラス方程式と言います。
両者ともに、電位の分布が分かれば、誘電率で除算することで空間電荷の分布も求められることを表しています。
具体的には、ラプラス方程式の場合は\(\Delta V=0\)となり、電位が一定または位置の一乗で変化する領域では電荷が存在しないことが分かります。
よく、pn接合半導体での電位分布、電場分布の計算にも用いられますが、電磁気学としても本問のように出題されることがあります。
解答に際して
変数分離法を用いて微分方程式を解くことに帰着します。
例えば、(1)式はラプラシアン\(\Delta\)が含まれているため、2階微分項になっています。このため、2回積分をすると電位が求まり、1回だけの積分でも\(E=-grad V\)より、電場が求まります。
不定積分のため、積分定数\(C\)が含まれますが、これは問題で与えられた境界条件を用いて、具体的な値を算出。消去することで、問題で与えられた条件下での特殊解が求められます。
解答例
a<r<bの範囲において、電荷が無いため、(1)式により
\begin{aligned}\Delta \phi=\dfrac{1}{r}\dfrac{\partial}{\partial r}\left(r \dfrac{\partial V}{\partial r} \right)+\dfrac{1}{r^{2}}\dfrac{\partial ^{2}V}{\partial \phi^{2}}+\dfrac{\partial^{2} V}{\partial z^{2}}=0\end{aligned}
電場はr方向に対して発生するため、z方向、θ方向は等電位になる。
\begin{aligned}\dfrac{\partial V}{\partial \phi}=\dfrac{\partial V}{\partial z}=0\end{aligned}
よって、(4)式は下記のように書き直すことができる。
\begin{aligned}\dfrac{1}{r}\dfrac{\partial}{\partial r}\left(r \dfrac{\partial V}{\partial r} \right)=0\end{aligned}
なお、電場はrに依存する関数のため、電位\(V\)もrに依存する関数\(V(r)\)になる。上式をrで積分し
\begin{aligned}\left(r \dfrac{\partial V(r)}{\partial r} \right)=A \\ V(r)=A\log(r)+B\end{aligned}
となる。(A,Bは積分定数)
これに対し、問題で与えられた境界条件\((V(a)=V_{o},V_{b}=0)\)を代入し
\begin{aligned}A=\dfrac{V_{o}}{\log(a/b)},B=–\dfrac{V_{o}\log b}{\log(a/b)}\end{aligned}
以上より、求める電位分布は下記のようになる。
\begin{aligned}V(r)=\dfrac{\log(r/b)}{\log(a/b)}V_{o}\end{aligned}
また、電場分布は、\(E(r)=-grad V(r)=-\dfrac{\partial V(r)}{\partial r}\)より
\begin{aligned}E=-\dfrac{V_{o}}{r\log(a/b)}\end{aligned}
最後に
本問は、ガウスの法則を用いた場合でも同様の結果になります。電荷Qを与えてガウスの法則で電場分布、電位分布を求めることで確かめることができます。
時間に余裕があれば、各自チャレンジしてみましょう。