導波管の性質とTEモード、TMモード、遮断周波数の計算問題

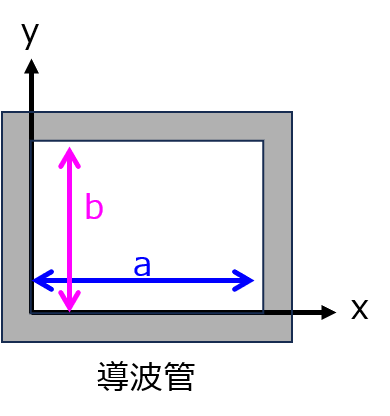
導波管とは

電磁波の伝送に用いる伝送路です。電磁場を通信源として見て、情報伝送などに用いられます。

無限平面型(スラブ型)もありますが、院試では矩形型の伝送路で問われることが多いです。型枠は金属管で覆われており、境界条件により電場を通さないようにしています。よって、型枠内部の中空領域において電磁波が伝搬します。

電磁波は、任意の周波数で伝搬するのではなく、決まった規則の周波数で離散的に伝搬します。下記では、その理由について深堀していきます。

導出の手順

問題で与えた内容が、実は導出そのものになっています。

(1)波動方程式

導波管は、マクスウェル方程式から導出できる波動方程式

\begin{aligned}\Delta \boldsymbol{E}-\varepsilon_{o}\mu_{o}\dfrac{\partial ^{2}\boldsymbol{E}}{\partial t^{2}}=0\end{aligned}

\begin{aligned}\Delta \boldsymbol{H}-\varepsilon_{o}\mu_{o}\dfrac{\partial ^{2}\boldsymbol{H}}{\partial t^{2}}=0\end{aligned}

の解を仮定することで、振る舞いが分かります。

※導出については、こちらの記事で詳しく説明しています。リンク先の問(3)で電信方程式を導出していますが、真空中だと導電率が0なので、波動方程式になります。覚えていない方は是非ともご覧ください。

(2)電場成分の一般解

導波管は、xy平面は導体で覆われています。このため、z方向にのみ伝搬する想定で、電場成分を下記のように立式します。(exp項内部が電磁波の伝搬成分を表す。)

\begin{aligned}E_{z}=E_{z}(x,y)e^{i(\beta z – \omega t)}\end{aligned}

これを式(1)に代入し、解くことで導波管内部の電場分布を知ることができます。

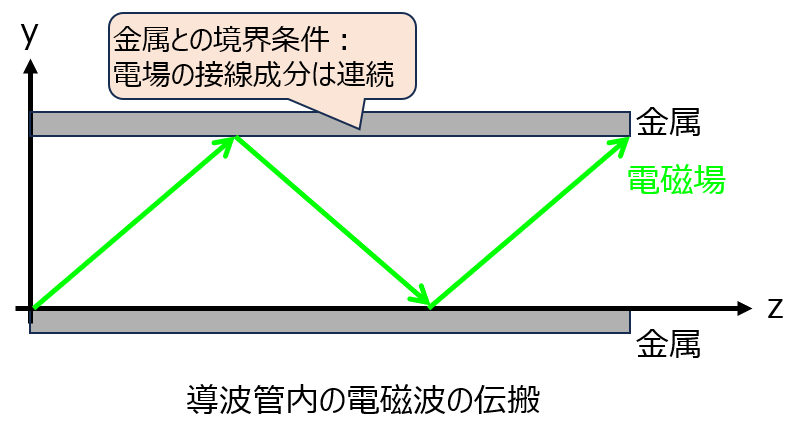
ただ、微分方程式のため、やみくもに手計算で解こうとすると闇にはまります。そこで、数学的なテクニックを用います。

微分方程式を解く際の常套手段である変数分離法を用い、電場成分\(E_{z}(x,y)\)を下記のように分解します。

\begin{aligned}E_{z}(x,y)=X(x)Y(y)\end{aligned}

これを(1)式に代入すると

\begin{aligned}Y(y)\dfrac{\partial^{2}}{\partial x^{2}}X(x)+X(x)\dfrac{\partial^{2}}{\partial x^{2}}Y(y)+\varepsilon_{o}\mu_{o}\omega^{2}=0\end{aligned}

\(k^{2}=\varepsilon_{o}\mu_{o}\omega^{2} , C_{y}=k^{2}-C_{x}\)とし、x,y項それぞれ

\begin{cases}\dfrac{\partial^{2}}{\partial x^{2}}X(x)=-C_{x}X \\ \dfrac{\partial^{2}}{\partial y^{2}}Y(y)=-C_{y}Y\end{cases}

と置きます。上記の第1式について、α>0の\(X(x)=e^{\alpha x}\)と置くと

\begin{aligned}\alpha^{2}=-C_{x} \\ \alpha=±i\sqrt{C_{x}}\end{aligned}

オイラーの式より、sin,cos項に分解できるため

\begin{aligned}X(x)=A\sin\sqrt{C_{x}}x+B\cos\sqrt{C_{x}}x\end{aligned}

と置ける。導波管の存在する領域では電場が0になる境界条件\(X(0)=X(a)=0\)を代入すると、\(B=0\)が導かれ、sin項についても\(\sqrt{C_{x}}a=m\pi\)になる。(mは自然数)

同様に、第2式についても、β>0の\(Y(y)=e^{\beta x}\)と置くことで、\(\beta=±i\sqrt{C_{y}}\)となり、一般解

\begin{aligned}Y(y)=C\sin\sqrt{C_{y}}x+D\cos\sqrt{C_{y}}x\end{aligned}

に対し、境界条件\(Y(0)=Y(b)=0\)を適用すると、

\begin{cases}D=0 \\ \sqrt{C_{x}}b=n\pi\end{cases}

以上より、求める電場成分は

\begin{aligned}E_{z}=AC\sin\dfrac{m\pi x}{a}\sin\dfrac{n\pi y}{b}\end{aligned}

※\(AC=E_{o}\)と置き、最終的な解とすることがあります。

n,mともに1以上で無いと電場成分が0になり、存在できないです。このような伝搬モードをTE波と言います。

(3)磁場成分の一般解

(2)と同じです。ただし、境界条件だけ異なります。

金属管内部に電場は存在しないので、(2)ではそのまま\(E_{z}=0\)を考えれば良かったですが、磁場の場合は話が変わります。

磁場\(H\)の法線成分は連続にならないこと\(\dfrac{\partial H}{\partial x}=0\)に注目します。(y軸成分の境界条件についても同様に\(\dfrac{\partial H}{\partial y}=0\)の偏微分を考えます。

すると、(8)式、(9)式を立式するところまでは同じですが、これを一度偏微分することから、三角関数項がsinとcosで入れ替わります。

ですので、最終的な解は、電場では(11)式のようにsin項で表現していましたが、磁場の場合はcos項になります。

\begin{aligned}H_{z}=AC\cos\dfrac{m\pi x}{a}\cos\dfrac{n\pi y}{b}\end{aligned}

cos項ですので、mかnがどちらか0であったとしても、もう一方が1以上であれば\(H_{z}\)は0より大きい値となり、伝搬します。(TM波と言います。)

上記の点は電場と異なりますので、是非覚えておきましょう。

(4)遮断周波数

問(2)(3)の結果から波数を導き、そこから遮断周波数を算出します。

TE波の場合

(2)(3)の結果により、電場、磁場はsin cosの違いは有れど、\(\dfrac{m\pi}{a},\dfrac{n\pi}{b}\)の波数を持っています。

よって、二つの重ね合わせ

\begin{aligned}k_{mn}^{2}=\left (\dfrac{m \pi}{a} \right)^{2}+\left (\dfrac{m \pi}{b} \right)^{2}\end{aligned}

について、遮断周波数\(f_{c}=\dfrac{c k_{mn}}{2 \pi}\)は

\begin{aligned}f_{c}=\dfrac{c}{2 \pi}\sqrt{\left (\dfrac{m \pi}{a} \right)^{2}+\left (\dfrac{m \pi}{b} \right)^{2}}\end{aligned}

なお、\(c\)は光速(3.0*10^8 m/s)である。最小値は、m=n=1を考えれば良く

\begin{aligned}f_{min}=\dfrac{c}{2 \pi}\sqrt{\left (\dfrac{\pi}{a} \right)^{2}+\left (\dfrac{\pi}{b} \right)^{2}}\end{aligned}

TM波の場合

(3)より、mかnどちらか0でも問題無いです。a>bで、逆数を取るので、1/aの方が小さいです。

よって、cos(mπ/a)に関わる項にm=1を代入し、n=0とすると、最小値

\begin{aligned}f_{min}=\dfrac{c}{2 \pi}\dfrac{\pi}{a}\end{aligned}

を得られます。

(5)分散関係

量子力学的要素が強く、工学部の院試にはあまり出ないとは思いますが、参考に記載します。工学部ではあまり習わないかもしれませんが、分散関係とは下記の意味になります。

上記は、相対論で述べられている式になります。内容を図示すると、下記のようになります。

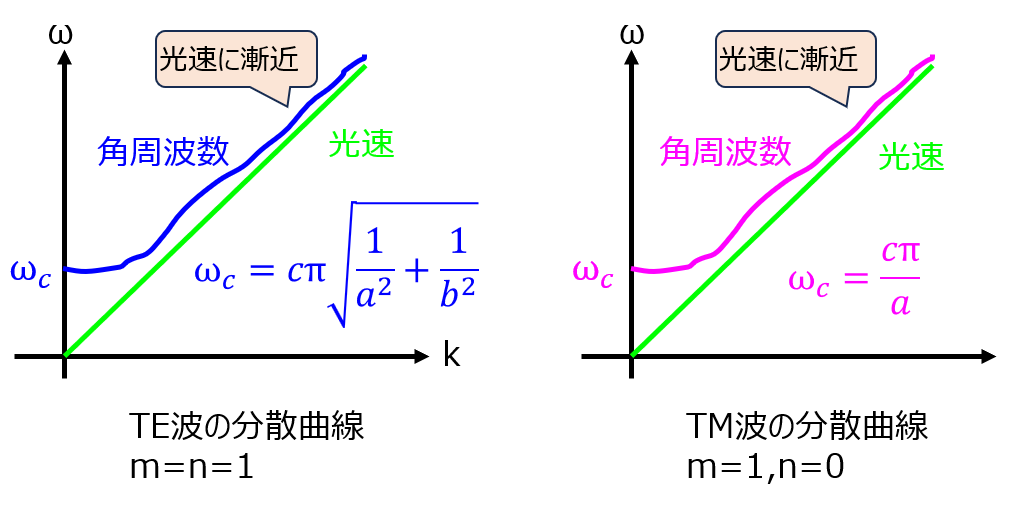
波数が小さい領域では、カットオフ角周波数に近づいているため、情報が伝搬しないことが分かります。

一方で、波数が大きくなるにつれて傾きが大きくなり、群速度\(\dfrac{d\omega}{dk}\)は光速に漸近します。よって、その分だけ情報を伝送できるようになります。

最後に

導波管は、上記のようなパターン問題での出題が非常に多いです。微分方程式の解き方を覚えているだけで得点することができます。是非、知識に入れておきましょう。