【情報理論】生成行列の求め方と誤り訂正方法、問題

生成行列とは

情報ビットから符号を生成するための行列です。

大前提として、本記事では情報理論の内、符号の誤りを検出する方法の一つを紹介します。

符号とは、情報を表す情報ビットと検査部分を表す検査ビットで分かれています。

検査行列を活用し、誤りを訂正する方法もありますが、本記事では生成行列から誤りを確認する方法を紹介します。

入力符号に生成行列を積算すると、取り得る出力を網羅的に入手できます。取り得る出力どれにも該当しない出力を検出する=誤りであることが分かる大方針の元、説明していきます。

生成行列の求め方

手順1：検査行列$\mathit{H}$を成分分解する

下記のように分解できます。

$$\begin{array}{}\text{(2)}& \begin{array}{r}\mathit{H}=[{\mathit{P}}^{\mathit{t}}\mathit{I}]\end{array}\end{array}$$

$\mathit{P}$は情報・検査ビット関連行列と言います。検査行列から生成行列を求める。またはその逆を行うために必ず出てくる行列です。キーになりますので覚えておきましょう。

検査行列は正方行列ではなく、列の数が行の数より多い行列です。

そのため、行の個数分を単位行列$I$で表しても、単位行列に属さない列が出てきます。その分を情報・検査ビット関連行列で表せば良いです。

手順2：${\mathit{P}}^{\mathit{t}}$を転置する

生成行列$\mathit{G}$は、下記のように表すことができます。

$$\begin{array}{}\text{(3)}& \begin{array}{r}\mathit{G}=[\mathit{I}\mathit{P}]\end{array}\end{array}$$

手順1で求めた情報・検査ビット関連行列(転置)をもう一度転置し、行の成分の数だけ単位行列を追加します。

生成する符号の組み合わせを生成行列を用いて求める

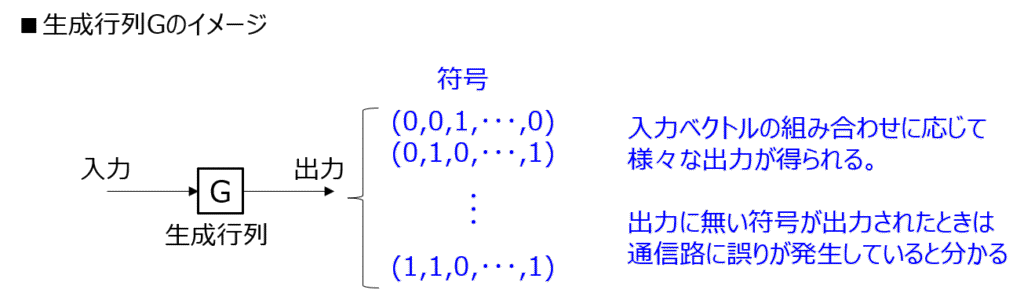
入力する符号ベクトルを$\mathit{c}$とすれば、下記の計算で生成する符号の候補を求めることができます。

$$\begin{array}{}\text{(4)}& \begin{array}{r}\mathit{c}G\end{array}\end{array}$$

求め方の例

例)3行1列ベクトル $\mathit{c}=(c_0,c_1,c_2)$と

生成行列$\mathit{G}=\left(\begin{array}{ccccc}1& 0& 0& 0& 1\\ 0& 1& 0& 1& 1\\ 0& 0& 1& 1& 1\end{array}\right)$を考える。

このとき、(4)式を計算すると

$$\begin{array}{}\text{(5)}& \begin{array}{r}(c_0,c_1,c_2,c_1\oplus c_2,c_0\oplus c_1\oplus c_2)\end{array}\end{array}$$になる。

$c_0{c}_2$は0,1しか取らないのだから、$2^3=8$通りの入力に対し(5)式は下記の出力しか取りえないです。

$c_0$	$c_1$	$c_2$	$c_1\oplus c_2$	$c_0\oplus c_1\oplus c_2$
0	0	0	0	0
0	0	1	1	1
0	1	0	1	1
0	1	1	0	0
1	0	0	0	0
1	0	1	1	0
1	1	0	1	0
1	1	1	0	1

もし、上記の出力以外が出てきたら、それは誤りであることが分かります。

注意点

本問は線形符号であることが前提です。そのため、$c_i$の和は排他的論理和で表すことが必要です。

線形関数についての詳しい記事は、こちらで説明しています。

解答例

(1)生成行列の求め方

行の個数は3つのため、単位行列は3*3成分である。

$\mathit{H}$は(7,3)成分のため、後半の5列目~7列目が単位行列成分

一方で、前半の1~4列目の部分は情報・検査ビット関連行列成分。

(2)式より

$$\begin{array}{}\text{(6)}& \begin{array}{r}{\mathit{P}}^{\mathit{t}}=\left(\begin{array}{cccc}1& 0& 1& 1\\ 1& 1& 1& 0\\ 0& 1& 1& 1\end{array}\right)\end{array}\end{array}$$

が得られる。(3)式により、$\mathit{G}$を求める。

$$\begin{array}{}\text{(7)}& \begin{array}{r}\mathit{P}=\left(\begin{array}{ccc}1& 1& 0\\ 0& 1& 1\\ 1& 1& 1\\ 1& 0& 1\end{array}\right)\end{array}\end{array}$$

行の個数が4つのため、単位行列は4*4成分。

$$\begin{array}{}\text{(8)}& \begin{array}{rl}\mathit{G}& =[\mathit{I},\mathit{P}]\\ & =\left(\begin{array}{ccccccc}1& 0& 0& 0& 1& 1& 0\\ 0& 1& 0& 0& 0& 1& 1\\ 0& 0& 1& 0& 1& 1& 1\\ 0& 0& 0& 1& 1& 0& 1\end{array}\right)\end{array}\end{array}$$

(2)符号語の生成

(1)より、行の成分は4つ。よって、入力符号$\mathit{c}$を

$$\begin{array}{}\text{(9)}& \begin{array}{r}\mathit{c}=(c_0,c_1,c_2,c_3)\end{array}\end{array}$$で4成分定義する。

この時の生成符号は

$$\begin{array}{}\text{(10)}& \begin{array}{rl}\mathit{c}\mathit{G}& =(c_0,c_1,c_2,c_3,c_0\oplus c_2\oplus c_3,c_0\oplus c_1\oplus c_2,c_1\oplus c_2\oplus c_3)\end{array}\end{array}$$

$c_i∊(0,1)$のため、考えられる生成符号は下記のパターンになる。

$c_0$	$c_1$	$c_2$	$c_3$	$c_0\oplus c_2\oplus c_3$	$c_0\oplus c_1\oplus c_2$	$c_1\oplus c_2\oplus c_3$
0	0	0	0	0	0	0
0	0	0	1	1	0	1
0	0	1	0	1	1	1
0	0	1	1	0	1	0
0	1	0	0	0	1	1
0	1	0	1	1	1	0
0	1	1	0	1	0	0
0	1	1	1	0	0	1
1	0	0	0	1	1	0
1	0	0	1	0	1	1
1	0	1	0	0	0	1
1	0	1	1	1	0	0
1	1	0	0	1	0	1
1	1	0	1	0	0	0
1	1	1	0	0	1	0
1	1	1	1	1	1	1

(3)誤り訂正

[1 1 1 1 1 1 0]は、(2)の符号語の一覧表に無いため、誤りである。

最もハミング距離が小さい符号は、[1 1 1 1 1 1 1]のため、これに訂正する。