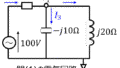
下記の電気回路(1)(2)について、端子1-1’に素子を接続した際に発生する端子1-1’間の電圧を答えよ。
(1)抵抗Rを接続している回路に、コンデンサ、コイルの並列回路を接続した時
(2)抵抗RとコイルLの並列回路に抵抗\(R_{L}\)を接続した時
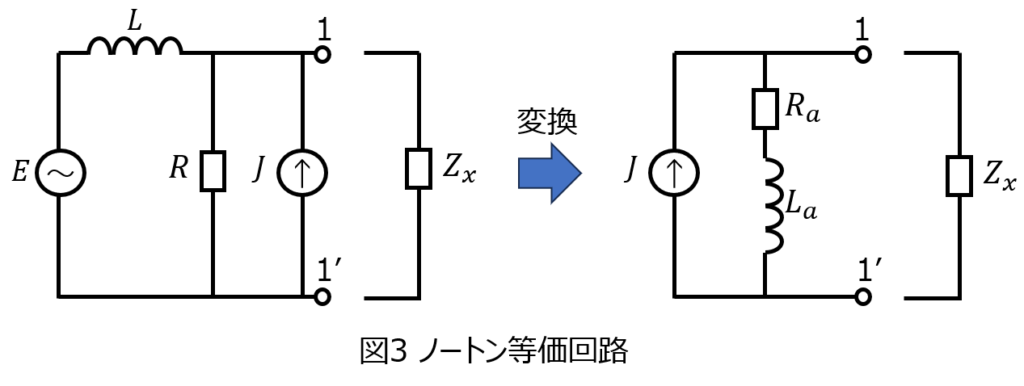
(3)下記の図3の電気回路について、端子1-1’間でノートンの定理を適用すると、図4に等価変換できるとする。このとき、抵抗\(R_{s}\)とコイル\(L_{s}\)の値を求めよ。
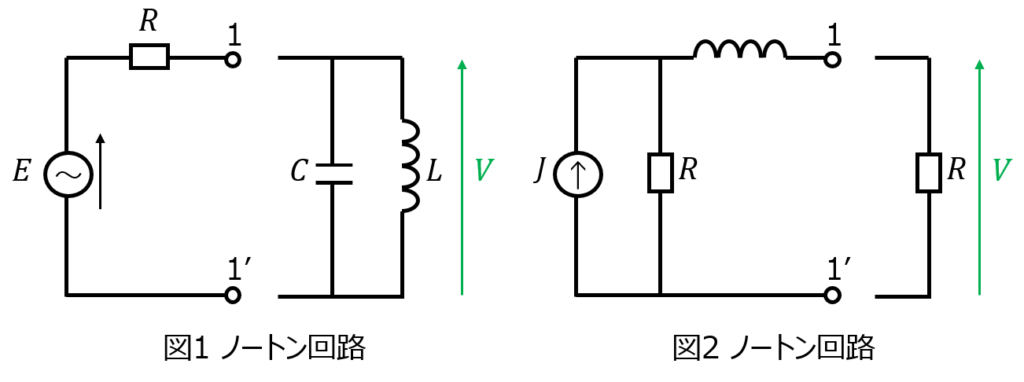
ノートンの定理について
ある端子間で発生する電圧は、その端子を短絡したときに流れる短絡電流にアドミタンス成分を除した式で表せる。というルールを言います。(ノルトンの定理とも呼びます。)
短絡電流を\(I_{s}\)、端子から左を見たアドミタンスを\(Y_{o}\)、接続する負荷のアドミタンスを\(Y_{L}\)とすると、端子間の電圧\(V\)は下記で示されます。
\begin{aligned}V=\dfrac{I_{s}}{Y_{o}+Y_{L}}\end{aligned}
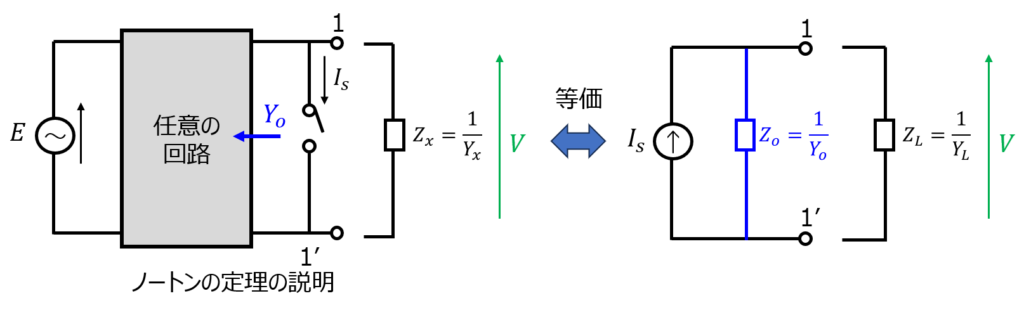
なお、端子から左を見たアドミタンスを計算する際は、電流源ならば開放。電圧源ならば短絡して考えます。これは、I=0,V=0の立場に対応しています。
重ね合わせの理でも同様の操作をしました。ノートンの定理でも忘れないようにしましょう。
定理の証明
任意の電気回路について、等価となるように回路素子を変更していくと、ノートンの定理で説明した等価回路に行きつくことで証明します。
まず、下記の回路モデルを考えます。一般性のため、ブラックボックス内は任意の形状の回路素子を接続できるものとします。
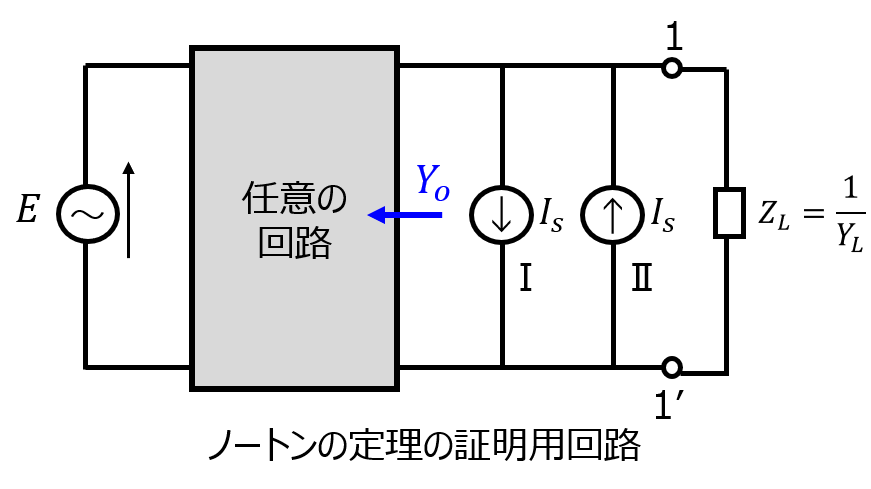
負荷\(Y_{L}\)側に電流源±Iをそれぞれ接続します。この状態で、上向きの電流源-Iを削除します。
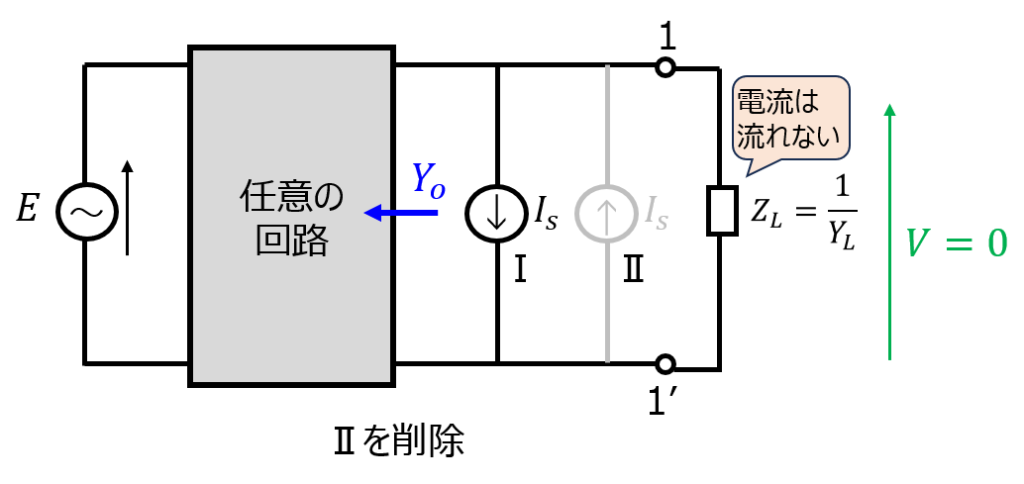
そうなると、端子1-1’間に短絡電流\(I_{s}\)が下向きに流れます。この時に負荷\(Y_{L}\)を接続しても流れる電流は無いため、端子1-1’で発生する電圧は0です。
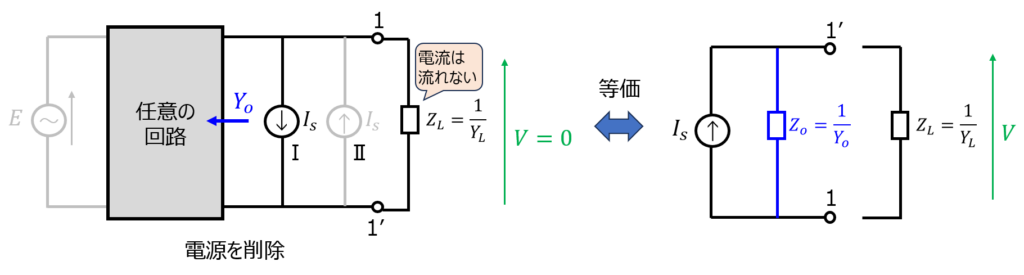
このとき、電源側の電圧源、電流源も削除すると、ノートンの定理を意味した等価回路が出来上がります。任意の電気回路は、ノートンの等価回路で示せることが分かりました。
テブナンの定理との双対性
重ね合わせの理より、ある節点で発生する電圧は
\begin{aligned}\begin{pmatrix} V_{1} \\ V_{2} \\ : \\ V_{n} \end{pmatrix}=\begin{pmatrix} z_{11} & z_{12} & \ldots & z_{1n} \\ z_{21} & z_{22} & \ldots & z_{2n} \\ \vdots & \ddots & \\ z_{n1} & z_{n2} & \ldots & z_{nn} \end{pmatrix}\begin{pmatrix} I_{1} \\ I_{2} \\ \vdots \\ I_{n} \end{pmatrix}\end{aligned}
で表されます。
一方で、電流源とアドミタンスの組み合わせにより
\begin{aligned}\begin{pmatrix} I_{1} \\ I_{2} \\ : \\ I_{n} \end{pmatrix}=\begin{pmatrix} Y_{11} & Y_{12} & \ldots & Y_{1n} \\ Y_{21} & Y_{22} & \ldots & Y_{2n} \\ \vdots & \ddots & \\ Y_{n1} & Y_{n2} & \ldots & Y_{nn} \end{pmatrix}\begin{pmatrix} V_{1} \\ V_{2} \\ : \\ V_{n} \end{pmatrix}\end{aligned}
にて回路方程式を表すことができます。
このような関係を双対性と言い、テブナンの定理の式、ノートンの定理の式
\begin{cases}I=\dfrac{V_{o}}{Z+Z_{o}} \\ V=\dfrac{I_{s}}{Y_{o}+Y_{L}}\end{cases}
も双対性に含まれます。つまり、ノートンの定理で表記した等価回路は、テブナン等価回路でも表記することができます。
問題によっては、複雑な電気回路も出てきます。そのとき、ノートンの定理、テブナンの定理、どちらの方が簡単に解けるか考える癖を付けましょう。
解答例
(1)コンデンサ、コイルの並列接続時
まず、端子1-1’から左を見たアドミタンス\(Y_{o}\)を求める。抵抗\(R\)のみ接続しているので
\begin{aligned}Y_{o}=\dfrac{1}{R}\end{aligned}
接続しようとするコイル、コンデンサの並列負荷のアドミタンス\(Y_{L}\)は
\begin{aligned}Y_{L}=\dfrac{1}{j \omega L}+j \omega C\end{aligned}
端子1-1’間を短絡したときに発生する短絡電流\(I_{s}\)は
\begin{aligned}I_{s}=\dfrac{E}{R}\end{aligned}
以上より、端子1-1’間に発生する電圧\(V\)は、ノートンの定理から
\begin{aligned}V&=\dfrac{I_{s}}{Y_{o}+Y_{L}} \\ &=\dfrac{E}{1+jR\left(\omega C-\dfrac{1}{\omega L}\right)}\end{aligned}
(2)抵抗\(R_{L}\)を接続したとき
(1)と同じようにして解きます。端子1-1’から左を見たアドミダンス\(Y_{o}\)は、電流源を開放するため
\begin{aligned}Y_{o}=\dfrac{1}{R+j \omega L}\end{aligned}
接続する素子は抵抗\(R_{L}\)であるため、アドミタンス\(Y_{L}\)は
\begin{aligned}Y_{L}=\dfrac{1}{R_{L}}\end{aligned}
端子1-1’を短絡したときに発生する短絡電流\(I_{s}\)は
\begin{aligned}I_{s}=\dfrac{R}{R+j \omega L}\end{aligned}
以上より、求める端子間電圧\(V\)は
\begin{aligned}V&=\dfrac{I_{s}}{Y_{o}+Y_{L}} \\ &=\dfrac{RR_{L}}{R_{L}+R+j \omega L}\end{aligned}
(3)等価アドミタンス
少し回路が複雑になりました。ノートンの定理と周辺知識を明確に理解していないと、間違えるかもしれません。
等価回路は電流源と並列であることからアドミタンスを求めたくなりますが、実際はインピーダンスで求めなければなりません。
端子1-1’から見たインピーダンス\(Z_{o}\)を考える。電流源は開放、電圧源は短絡するため、コイルLと抵抗Rの並列回路に見える。
\begin{aligned}Z_{o}&=\dfrac{j \omega L R}{R+ j \omega L} \\ &= \dfrac{\omega^{2} L^{2} R}{R^{2}+\omega^{2} L^{2}}+j \omega \dfrac{L R^{2}}{R^{2}+\omega^{2}L^{2}}\end{aligned}
これが等価回路のインピーダンス\(Z_{a}\)に等しい。
\begin{aligned}Z_{a}=R_{a}+j \omega L_{a}\end{aligned}
で表されるので、両者を比較して
\begin{cases}R_{a}=\dfrac{\omega^{2} L^{2} R}{R^{2}+\omega^{2}L^{2}} \\ L_{a}=\dfrac{LR^{2}}{R^{2}+\omega^{2} L^{2}}\end{cases}