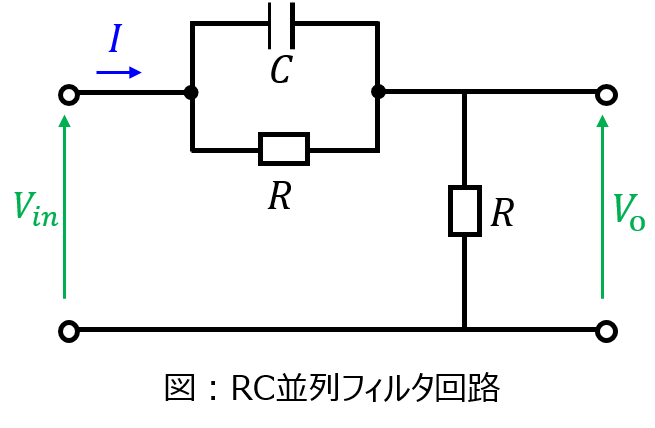
下記の電気回路のフィルタの種類を答えよ。
フィルタとは
入力信号のある周波数は遮断し、特定の周波数は出力する回路を言います。センサのノイズ処理など、様々な電気機器制御に使用されています。
通す周波数成分ごとに下記3通りのフィルタがあります。
- 低域通過フィルタ (低周波の入力のみ通す)
- 高域通過フィルタ (高周波の入力のみ通す)
- 帯域通過フィルタ (特定の周波数帯のみ通す)
それぞれ、下記で説明していきます。
低域通過フィルタ
前段の説明の通り、高周波成分は遮断する回路を言います。(ローパスフィルタとも言います。)
回路構成
下記に低域通過フィルタの例を示します。いくつかのパターンはありますが、出力側にコンデンサが付いていることが多いです。コンデンサのインピーダンスは、\(\frac{1}{j \omega C}\)で表されます。周波数が大きいほど、インピーダンスが小さくなり、電圧\(V_{o}\)が立たなくなります。一方で、低域の周波数ほど\(V_{o}\)に寄与するわけですから、このようにして低域周波数成分のみを出力電圧として取り出すわけですね。
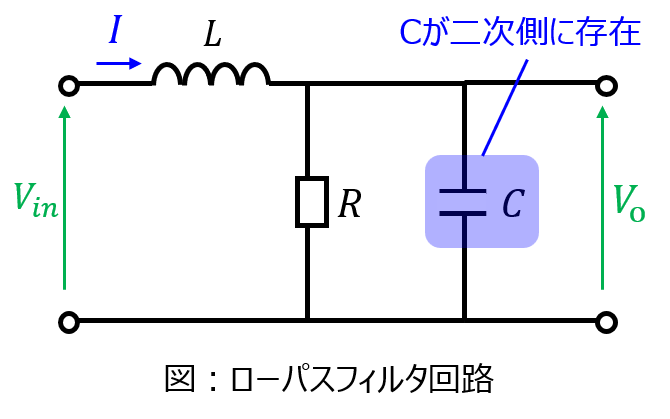
なお、入力側にインダクタが付いていることもあります。インダクタのインピーダンスは\(\j \omega L\)で表されるわけですから、高周波成分になるほど大きなインピーダンスになります。このようにして、Cに流れる前にも事前にLで高周波を阻止する二段構えの型で回路を作成することもあります。
低域通過フィルタの原理
入力成分\(V_{in}\)に対する出力成分\(V_{o}\)の比\(\dfrac{V_{o}}{V_{i}}\)を考えます。なお、簡単化のため、\(L=2CR^{2}\)とします。
入力端から右を見たインピーダンスは
\begin{aligned}Z=j \omega L+\dfrac{R}{1+j \omega CR}\end{aligned}
ここで、\(V_{in},V_{o}\)とインダクタにかかる電圧\(V_{L}\)の関係は
\begin{aligned}V_{in}&=V_{L}+V_{o}\end{aligned}
\begin{aligned}V_{o}&=V_{in}-\dfrac{j \omega L}{Z}V_{in} \\ &=\dfrac{R}{R(1-\omega^{2}LC)+j \omega L}\end{aligned}
これの絶対値は、実部と虚部の絶対値を取って
\begin{aligned}\left|\dfrac{V_{o}}{V_{in}}\right|&=\dfrac{R}{\sqrt{\omega^{4}L^{2}C^{2}R^{2}+R^{2}+\omega^{2}L(L-2CR^{2})}} \\ &=\dfrac{1}{\sqrt{\omega^{4}L^{2}C^{2}+1}}\end{aligned}
角周波数\(\omega\)を0に近づけた時、上式は1になるため、低周波の成分は減衰しないことが分かります。
一方で、\(\omega\)を∞に近づけると分母が大きくなりますので、結果は0になります。高周波は遮断することが分かりました。
角周波数が分母にのみ存在することから、積分回路と呼ばれることもあります。
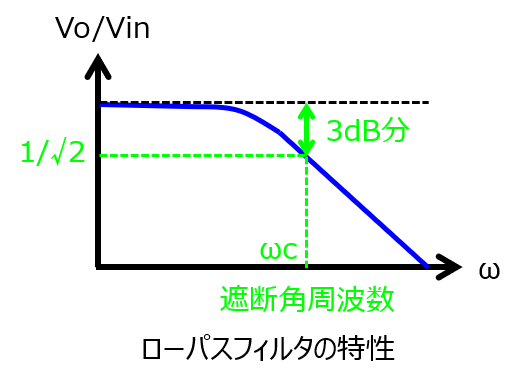
遮断角周波数
\(\left|\dfrac{V_{o}}{V_{in}}\right|\)が\dfrac{1}{\sqrt{2}}\)を与える角周波数\(\omega_{c}\)を遮断角周波数と言います。これ以上周波数を高めると、出力電圧が著しく減衰することから、閾値のような扱いをしています。
結局、周波数に対する入出力特性は下記のようになります。
オペアンプを用いた低域通過フィルタ
集中定数回路だけでなく、オペアンプを使用してもローパスフィルタを構成可能です。オペアンプの下流(2次側)にコンデンサCを置けば良く、集中定数回路と同じ考え方です。
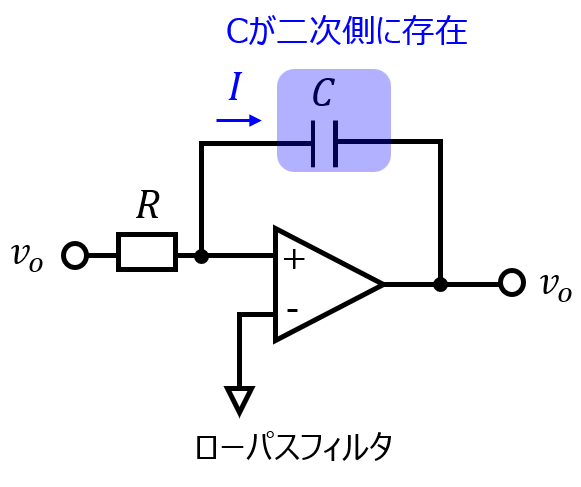
このとき、出力電圧\(V_{o}\)は
\begin{aligned}V_{o}=-\dfrac{1}{CR}\int V dt\end{aligned}
より、入力電圧を積分した出力電圧が得られます。(積分回路)
高域通過フィルタ
ハイパスフィルタとも言います。ローパスフィルタと逆で、高周波成分のみ通すフィルタです。
高域通過フィルタの原理
下記に回路構成を示します。よくあるパターンとして、入力側にコンデンサを置き、出力側に抵抗をおくパターンです。
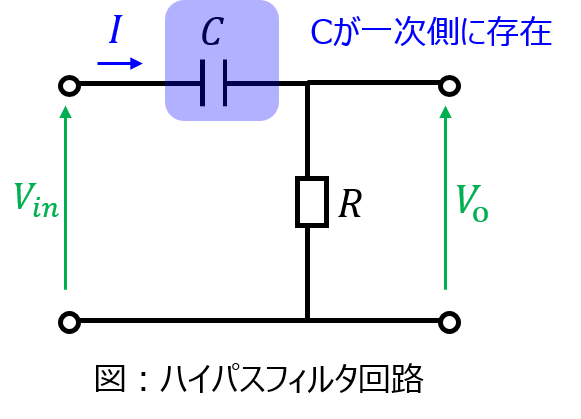
この時、低域通過フィルタと同様の計算を行うと、入力電圧に対する出力電圧の比は
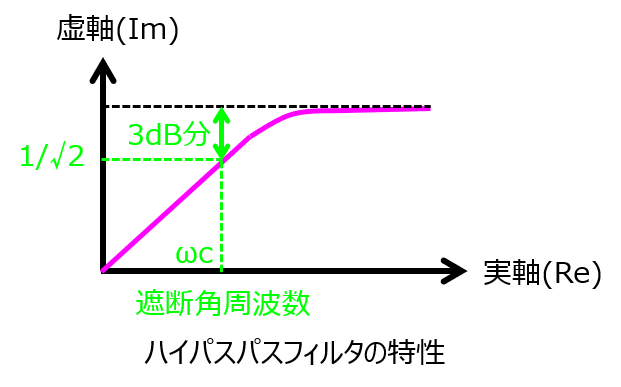
\begin{aligned}\left|\dfrac{V_{o}}{V_{in}}\right|=\dfrac{ \omega CR}{\sqrt{1+ (\omega CR)^{2}}}\end{aligned}
上式により、\(\omega=0\)のときは出力0、\(\omega\)を∞に近づけた時は出力1になります。ローパスフィルタと逆の特性になることが分かりましたね。
周波数の項が分子に存在することから微分回路と呼ばれることもあります。
オペアンプを用いた高域通過フィルタ
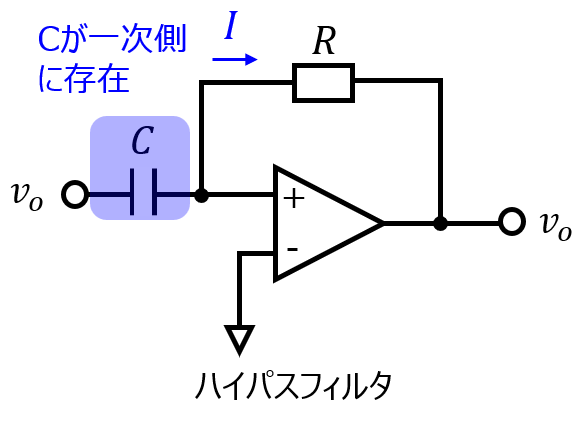
オペアンプの上流にコンデンサCを、下流に抵抗Rを置けば良いです。
この結果、出力電圧\(V_{o}\)は
\begin{aligned}V_{o}&=-RI \\ &=-RC\dfrac{dV_{i}}{dt}\end{aligned}
となり、微分回路であることが確かめられました。
帯域通過フィルタ
低域通過フィルタと高域通過フィルタを組み合わせて実現します。
下記に回路構成を示します。左にハイパスフィルタ、右にローパスフィルタを接続します。(左右のCとRの素子定数はそれぞれ同じ。)
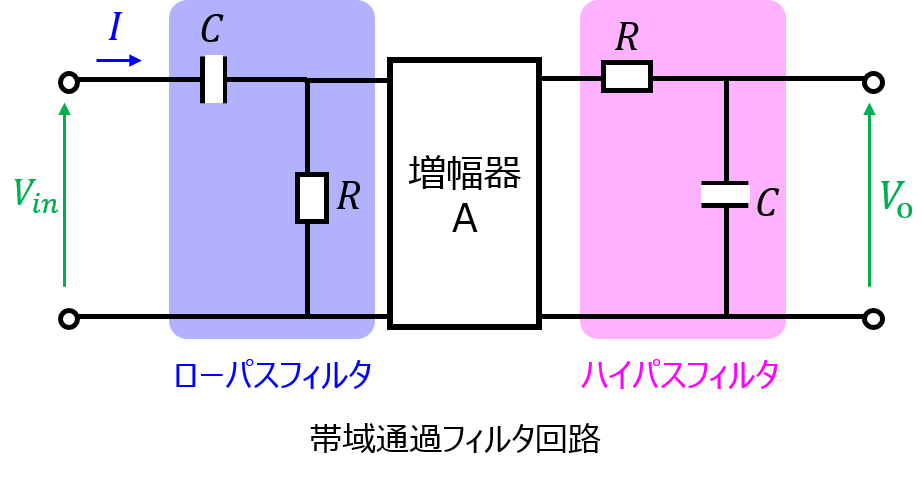
このとき、中間周波数帯ではそれほど出力が減衰しないことが予想できます。ただし、必要に応じて増幅器を中央に置き、出力を補償する場合があります。
回路の入力電圧と出力電圧の比は、ハイパスフィルタのみの場合とローパスフィルタのみの場合の比を乗算すれば良いので
\begin{aligned}\left|\dfrac{V_{o}}{V_{in}}\right|=A\dfrac{1}{\sqrt{1+\left(\dfrac{1}{\omega RC}\right)^{2}}\sqrt{1+(\omega RC)^{2}}}\end{aligned}
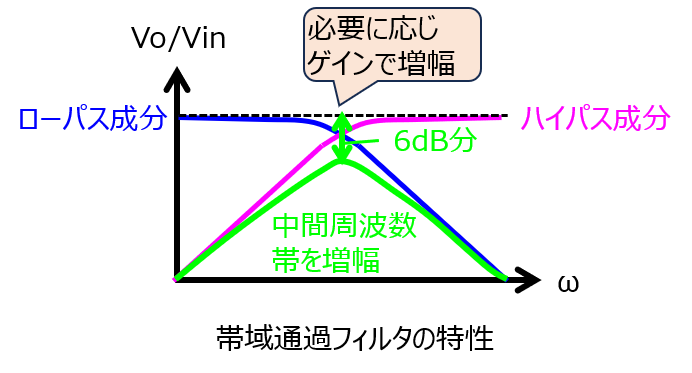
このときの周波数特性は下記になります。山なりになり、中間周波数帯域でのみ信号を通すことが分かりました。
解答例
問題で与えられた回路は、どれに該当するのでしょうか。今までの説明で、計算しなくても分かったかもしれません。結論:ハイパスフィルタになります。入力側にコンデンサがある時点で予想がつきますね。
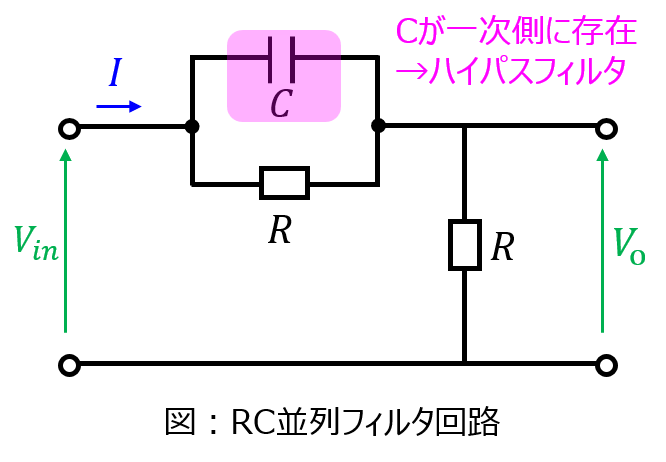
一応、下記で数式的に計算してみて、確かめてみましょう。
回路にある電流Iが流れている時、入力電圧\(V_{in}\)、出力電圧\(V_{o}\)は
\begin{aligned}V_{o}=RI\end{aligned}
\begin{aligned}V_{in}=RI+\dfrac{R}{1+j \omega CR}I\end{aligned}
以上より、両者の比は
\begin{aligned}\left|\dfrac{V_{o}}{V_{in}}\right|&=\dfrac{1}{1+\dfrac{1}{1+j \omega CR}} \\ &=\dfrac{1+j \omega CR}{2+j \omega CR}\end{aligned}
\(\omega=0\)のとき、上式は1/2だが、∞に近づけていくと1になる。
よって、ハイパスフィルタであることが確認できた。
最後に
問題にもあるように、RとCを適切に組み合わせれば、ある周波数帯の成分を半分くらいは通すフィルタも設計することができます。
将来、技術職に就いた時に適切なフィルタ設計を行うための素養になれば幸いです。