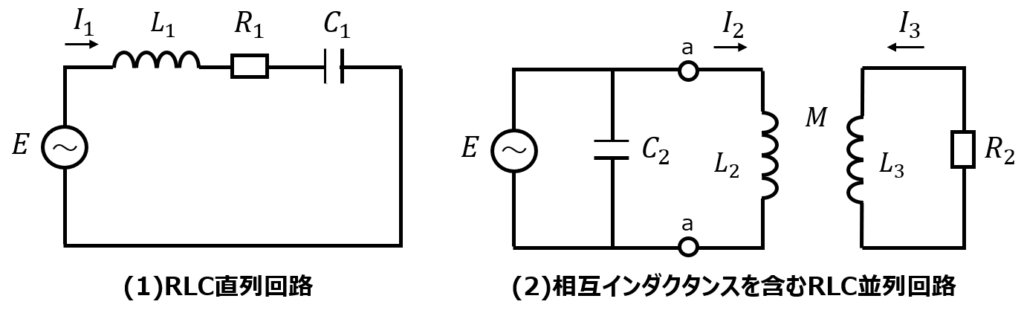
下記2つの共振回路のQ値を求めよ。
(1)RLC直列回路 \(R=2[\Omega],L=10[mH],C=1[μF]\)
(2)相互インダクタンスを含むRLC並列回路 ただし、\(R_{2} \gg \omega L\)とする。
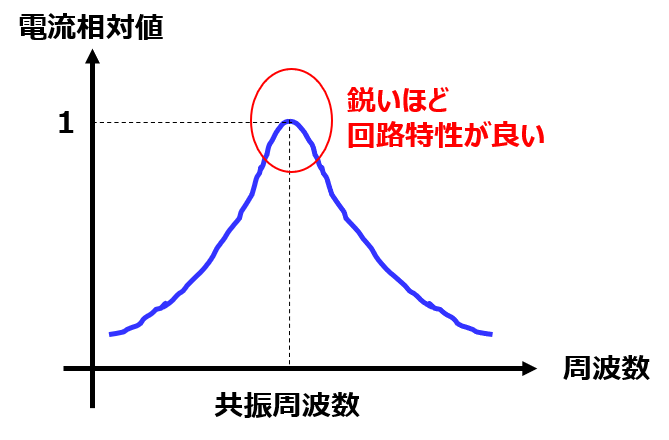
Q値とは
周波数に対する電気回路の共振の鋭さを指しています。鋭いほど良い回路(抵抗による損失が少ない)とされています。
共振回路の特性を考えるうえで非常に重要なパラメータです。
この記事で覚えたいこと
- 直列共振回路のQ値は、\(Q=\frac{\omega L}{R}\)で表される。
- 並列共振回路のQ値は、\(Q=\omega CR=\frac{\omega C}{G}\)で表される。
- 実際には電源電圧をかけて、\(Q=\frac{\omega CE}{GE}=\frac{I_{C}}{I}\)として計算することが多い。
Q値は、抵抗成分に対するインダクタ成分の比でも表すことができます。実際に問題を解くうえでは、直列共振回路はこの関係をそのまま使うと良いです。
並列共振回路は、インダクタ成分に対する抵抗成分の比と、分数が反対になります。このままでも解くことはできますが、共振周波数\(\omega=\sqrt{LC}\)の関係を用い、キャパシタ成分に対するコンダクタンス成分の比と考えるほうが解きやすくなります。
イメージとしては、抵抗Rに流れる電流が少なくなるほどQ値が高い側になります。(損失が少ないため)
Q値の考えを利用した電気機器(実用先)
アンテナ
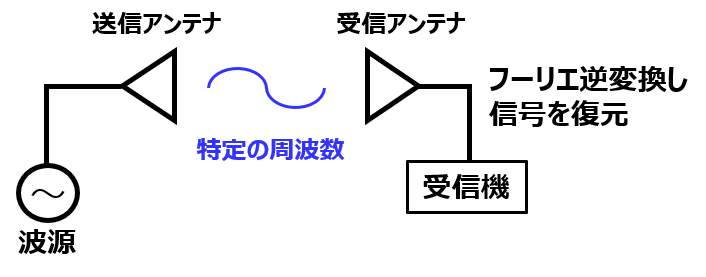
Q値の考えを利用すると、ある周波数帯で損失少なく電気信号を送信することができます。これを利用し、特定の周波数帯に情報を符号化し、送信側と受信側で回路を組むと、受信側で情報を受け取ることができます。
これをアンテナと言います。日常で広く用いられており、私たちの生活に欠かせないものとなっています。
非接触給電
アンテナは、電気信号を情報源として活用していました。一方で、非接触給電は、電気をエネルギーとして送信します。
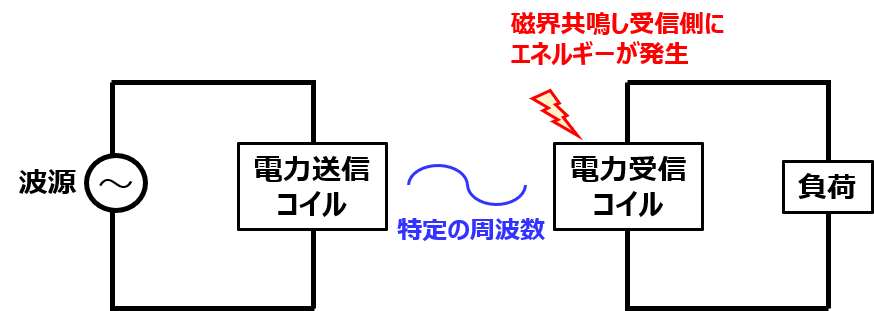
1次側と2次側でコイルを立てて、1次側で電圧をかけると、ある周波数の磁界が発生します。遠方に、同じ共振周波数の回路がある場合、磁気を通して共振し、エネルギーを受け取ることができます。
既に紹介した通り、直列回路のQ値は、\(Q=\dfrac{\omega L}{R}\)になります。この式から
- 共振周波数が大きいこと
- インダクタンスLが大きいこと
- 抵抗Rが小さいこと
以上3条件により、高いQ値を実現できます。
高Q値化への課題
CHECK項目を見ると、紹介した3つのパラメータをQ値が大きくなる側に振ると、簡単に高Q値になりそうです。しかし、実際は簡単にいきません。
周波数を大きくすることによる課題
ジュール損以外に渦電流損とヒステリシス損からなる交流損失が発生します。
よって、際限なく大きくして良いものではありません。
インダクタンスLを大きくすることによる課題
インダクタンスLは、ソレノイドコイルの場合下記の式で表すことができます。
\begin{eqnarray}L=\mu_{0}N^2Sl\end{eqnarray}
- 高い透磁率の材料を選定する。
- 巻き数を多くする。
- 鎖交磁束の面積を大きくする。
- コイル長を長くする。
以上の4要素で大きくできますが、どれもスペース的な制約を受けます。
よって、同じく際限なく大きくすることはできません。
抵抗Rを小さくすることによる課題
抵抗Rは、物質によって決まります。
導電率の高い物質を使用することで、高いQ値を実現できます。
ただし、共振周波数の項目で説明した交流損失の影響が大きくなります。
渦電流損はなかなか減衰しなくなり、ヒステリシス損失も変わらずかかります。
よって、単に導電率の高い物質を利用すると良いわけではありません。
解答例
(1) RLC直列回路のQ値
回路全体のインピーダンスは
\begin{eqnarray}Z_{a}=R+j(\omega L-\dfrac{1}{\omega C}\end{eqnarray}
虚部=0のとき、共振周波数は、
\begin{eqnarray}\omega_{0}=\dfrac{1}{\sqrt{LC}}\end{eqnarray}
2章で紹介した式にパラメータを代入すれば良いので
\begin{eqnarray}Q=\dfrac{\omega L}{R}=\dfrac{10*10^{-3}}{2*10^{-4}}=50\end{eqnarray}
(2) 相互インダクタンスを含むRLC並列回路のQ値
まず、端子aより右のインピーダンス\(Z_{a}\)を求める。
回路方程式は以下のように表せる
\begin{cases}V_{a}=j\omega L_{2}I_{2}+j\omega MI_{3}\\ -R_{2}I_{3}=j\omega MI_{2}+j\omega L_{3}I_{3}\end{cases}
第2式を変形し
\begin{eqnarray}I_{3}=\dfrac{-j\omega MI_{2}}{R_{2}+j\omega L_{3}}\end{eqnarray}
これを(5)式に代入すると
\begin{eqnarray}Z_{a}=\dfrac{V_{a}}{I_{2}}=j\omega L_{2}+\dfrac{\omega ^{2}M^{2}}{R_{2}+j\omega L_{3}}\end{eqnarray}
\(R\gg \omega L_{2}\)のとき
\begin{eqnarray}Z_{a}=j\omega L_{2}+\dfrac{\omega ^{2}M^{2}}{R_{2}}\end{eqnarray}
これより、回路全体のアドミタンスは
\begin{aligned}Y&=j\omega C_{2}+\dfrac{R_{2}}{\omega^{2}M^{2}+j\omega L_{2}R_{2}}\\ &=j\omega C_{2}+\dfrac{R_{2}\left( \omega^{2}M^{2}-j\omega L_{2}R_{2}\right) }{\left( \omega ^{2}M^{2}\right) ^{2}+\omega ^{2}L_{2}^{2}R_{2}^{2}}\end{aligned}
虚部=0を考えると
\begin{aligned}C_{ 2}=\dfrac{L_{2}R_{2}^{2}}{\left( \omega ^{2}M^{2}\right) +\omega ^{2}L_{2}^{2}R_{2}^{2}} \end{aligned}
このとき、回路全体に流れる電流\(I\)は
\begin{aligned}I&=\dfrac{\omega^{2}MR_{2}E}{\left( \omega ^{2}M\right) ^{2}+\omega ^{2}L_{2}^{2}R_{2}^{2}}\\ &=\dfrac{\omega^{2}M^{2}R_{2}C_{2}E}{L_{2}R_{2}^{2}} \\ &=\dfrac{\omega ^{2}M^{2}C_{2}E}{L_{2}R_{2}}\end{aligned}
これより、求める共振回路のQは
\begin{eqnarray}Q=\dfrac{W_{0}C_{2}}{G}=\dfrac{\omega_{0}C_{2} E}{GE}=\dfrac{I_{C}}{I}\end{eqnarray}だから
\begin{eqnarray}Q=\dfrac{\omega_{0}C_{2}E}{\dfrac{\omega _{0}^{2}M^{2}C_{2}E}{L_{2}R_{3}}}=\dfrac{L_{2}R_{2}}{\omega _{0}M^{2}}\end{eqnarray}
ただし、\(\omega_{0}\)は(10)式を解いて
\begin{eqnarray}\omega_{0}=\sqrt{\dfrac{-C_{2}L_{2}^{2}R_{2}^{2}\pm \sqrt{C_{2}^{2}L_{2}^{4}R_{2}^{4}+4C_{2}L_{2}M^{4}R_{2}^{2}}}{2C_{2} M^{4}}}\end{eqnarray}
補足:求めたQ値 (13)式の解釈
等価回路は下記のようになります。
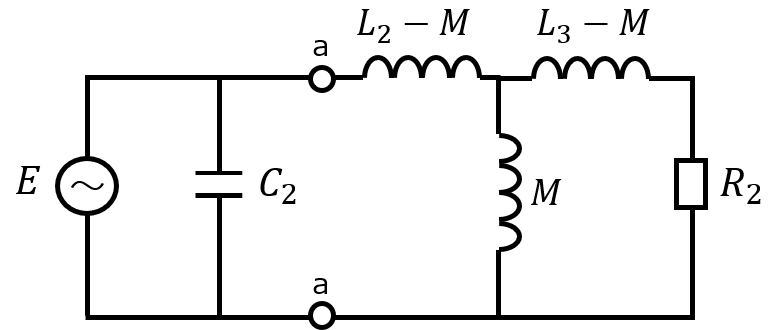
Rに流れる電流値が少ないほどQ値は大きくなります。
\(L_{2},R_{2}\)を大きくすると、コンデンサCに電流が流れる割合が増加し、イメージと合致します。
\(M\)を小さくすると、\(L_{2},L_{3}\)が大きくなり、Rに流れる電流が減少し、イメージと一致します。
また、共振周波数は(14)式で与えられ、Cのオーダーは2乗であることから分母のMが支配的になります。Mが大きくなると、共振周波数は小さくなるため、これもQ値が大きくなります。イメージと合致します。
最後に
Q値の設計は、実学を通して学ぶ要素が強いです。本問を通して回路設計に興味を持つ方が現れると嬉しいです。
参考文献
大学課程 電気回路(1):大野 克郎(著),西 哲生(著) 第5章


