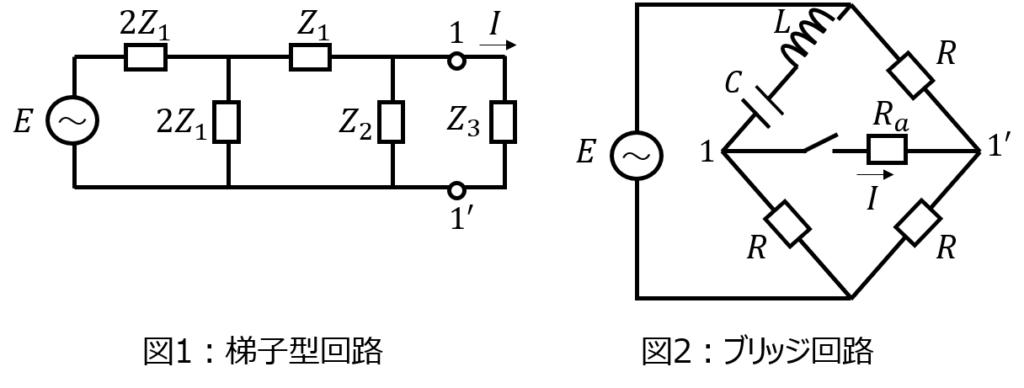
(1)下記の梯子型回路の端子1-1’にインピーダンス\(Z_{3}\)を接続する。このとき、\(Z_{3}\)に流れる電流を求めよ。
(2)下記のブリッジ型回路の端子1-1’に抵抗\(R_{a}\)を接続する。このとき、\(R_{a}\)に流れる電流を求めよ。
テブナンの定理とは
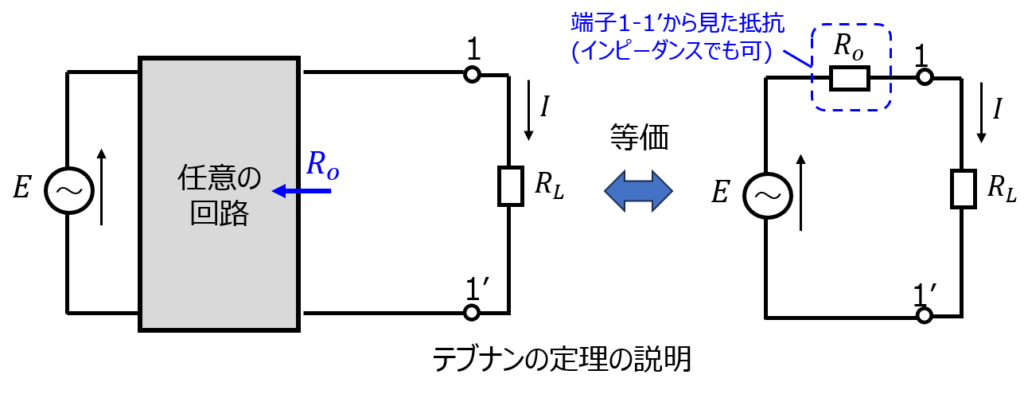
どんな回路でも、任意の2点から回路全体を見る時、ある起電力とインピーダンスを持つ電源に変換できる法則を言います。(ヘルムホルツの定理とも呼ばれます。)
これにより、ある端子間に素子を繋ぐときに流れる電流は、下記3つの操作で求められます。
- 注目している端子間を開放したときの端子間電圧\(V_{o}\)を求める。
- 注目している端子間から回路を見た時のインピーダンス\(Z_{o}\)を求める。
- 端子間に\(Z_{L}\)を接続した時に流れる電流は、下記になる。
\begin{aligned}I=\dfrac{V_{o}}{Z_{o}+Z_{L}}\end{aligned}
なお、2.の操作をするときは、重ね合わせの理を使用するときと同じく、電圧源は短絡、電流源は開放します。
テブナンの定理の証明
下記の電気回路モデルを考えます。箱の内部は任意の回路を示します。(ブラックボックス)
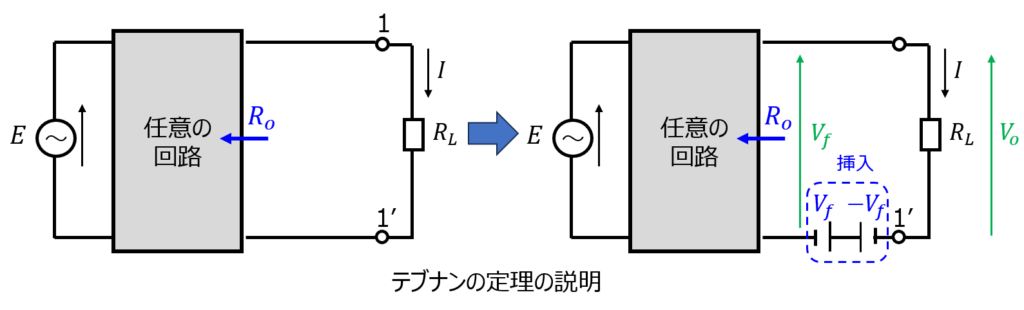
負荷\(R_{L}\)の下流に正負の向きを持つ端子電圧に等しい電圧源を挿入します。このとき、変換前の回路と等価になります。
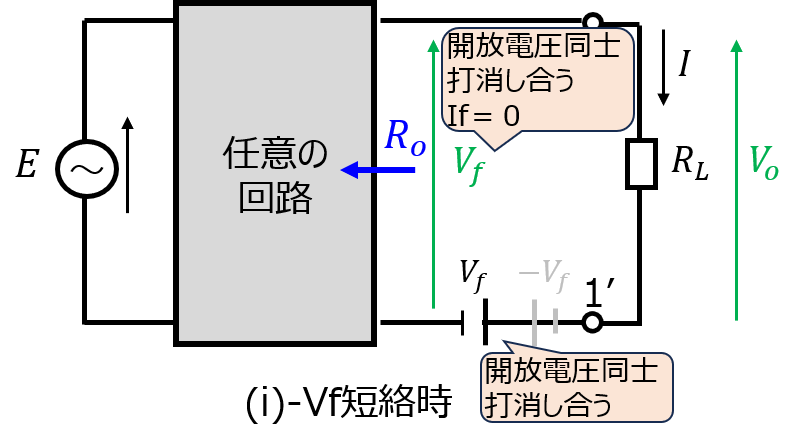
(i)2次側向きの電圧源\(-V_{f}\)を短絡した時、端子1-1’間の電位差は0になるので電流は流れません。
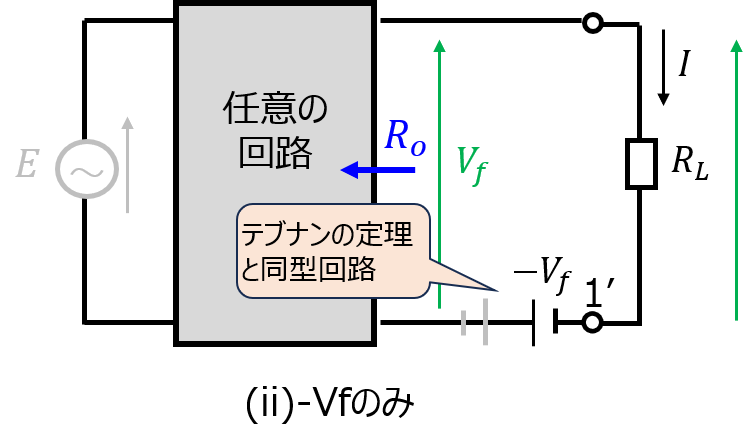
(ii)逆に、2次側向きの電圧源\(-V_{f}\)のみ残し、電源側の電圧源と\(V_{f}\)を削除すると、\(R_{L}\)に流れる電流は
\begin{aligned}I_{o}=\dfrac{V_{o}}{R_{o}+R_{L}}\end{aligned}
になります。重ね合わせの理より、端子1-1’に流れる電流は(i)(ii)の重ね合わせで、(i)は電流0なので、(ii)のみ結果に影響します。これは、前節で述べたように端子側から見た電圧、インピーダンスと同じになります。
元々与えられていた電気回路の等価変換を繰り返すことにより、テブナンの等価回路を示すことができました。(証明完了)
使用する際の注意点
証明の流れからも分かりますが、注目する端子から見た開放電圧、インピーダンスを求めなければなりません。
時間が経ち理解があやふやになると、電気回路の左から見たインピーダンスなどを求めたくなります。しかし、実際そんなことはありません。忘れないようにしましょう。
解答例
(1)梯子型回路
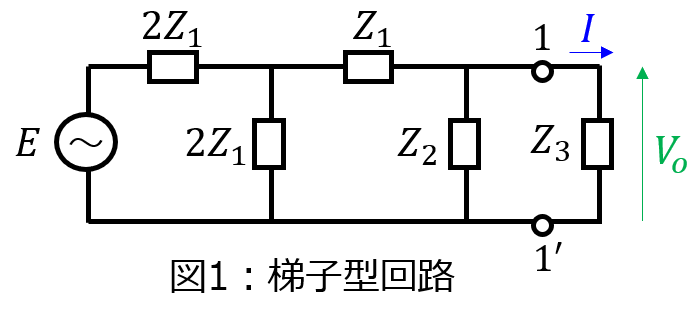
まず、端子1-1’間の開放電圧\(V_{o}\)を考える。分圧の法則により
\begin{aligned}V_{o}&=\dfrac{\dfrac{2Z_{1}(Z_{1}+Z_{2})}{2Z_{1}+Z_{1}+Z_{2}}}{2Z_{1}+\dfrac{2Z_{1}(Z_{1}+Z_{2})}{2Z_{1}+Z_{1}+Z_{2}}}\dfrac{Z_{2}}{Z_{1}+Z_{2}}E \\ &=\dfrac{2Z_{1}(Z_{1}+Z_{2})}{2Z_{1}(3Z_{1}+Z_{2})+2Z_{1}(Z_{1}+Z_{2})}\dfrac{Z_{2}}{Z_{1}+Z_{2}}E \\ &=\dfrac{Z_{2}E}{4Z_{1}+2Z_{2}} \end{aligned}
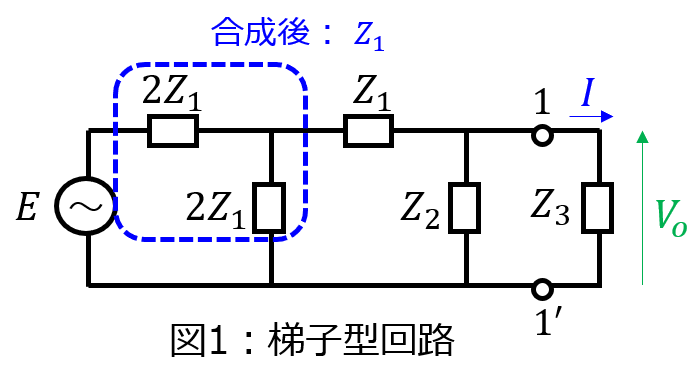
次に、端子1-1’間から見たインピーダンス\(Z_{o}\)を考える。\(2Z_{1}\)の並列回路の合成抵抗は\(Z_{1}\)だから
\begin{aligned}Z_{o}=\dfrac{2Z_{1}Z_{2}}{2Z_{1}+Z_{2}}\end{aligned}
以上より、インピーダンス\(Z_{3}\)を接続したときに流れる電流は
\begin{aligned}I&=\dfrac{V_{o}}{Z_{o}+Z_{3}} \\ &=\dfrac{Z_{2}E}{4Z_{1}Z_{2}+2(2Z_{1}+Z_{2})Z_{3}}\end{aligned}
(2)ブリッジ回路に流れる電流
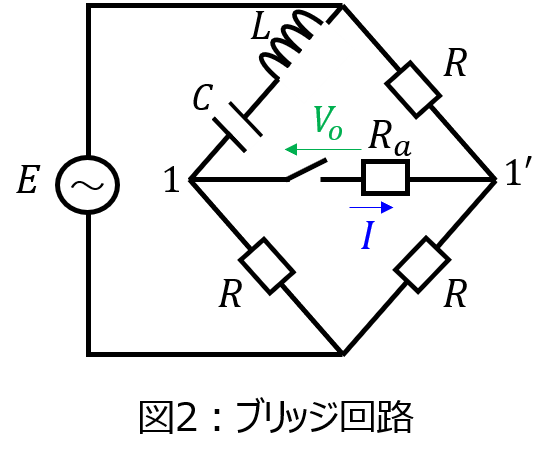
本問は、よく院試に出てきます。平衡条件も合わせて考える必要があるため、出題者から見て様々な知識を問うことができるからです。
端子1-1’間の電圧\(V_{o}\)は
\begin{aligned}V_{o}=\dfrac{R}{R+j \omega L + \dfrac{1}{j \omega C}}E-\dfrac{1}{2}E\end{aligned}
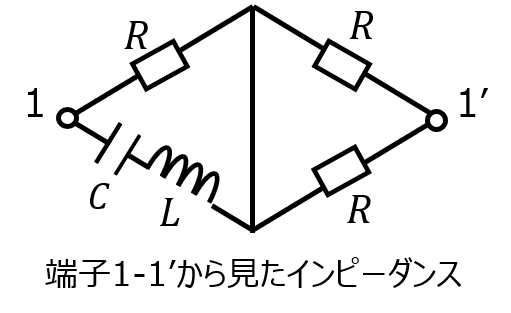
端子1-1’から見たインピーダンス\(Z_{o}\)は
\begin{aligned}Z_{o}&=\dfrac{R\left(j \omega L+\dfrac{1}{j \omega C} \right)}{R+ j \omega L +\dfrac{1}{j \omega C}}+\dfrac{R^{2}}{R+R} \\ &= \dfrac{R(1-\omega^{2}LC)}{1-\omega^{2}LC+j \omega CR}+\dfrac{R}{2}\end{aligned}
上記を用いて、\(R_{a}\)を接続したときの電流
\begin{aligned}I=\dfrac{V_{o}}{R_{a}+Z_{o}}\end{aligned}
を求めることができる。
最後に
試験で血迷うと、どの間の端子電圧、インピーダンスを求めるのかど忘れしてしまうかもしれません。
必ず、端子間から見たパラメータを求めます。自信を持って答えましょう。