下記の電気回路において、電流計Aに電流が流れないための条件を求めよ。
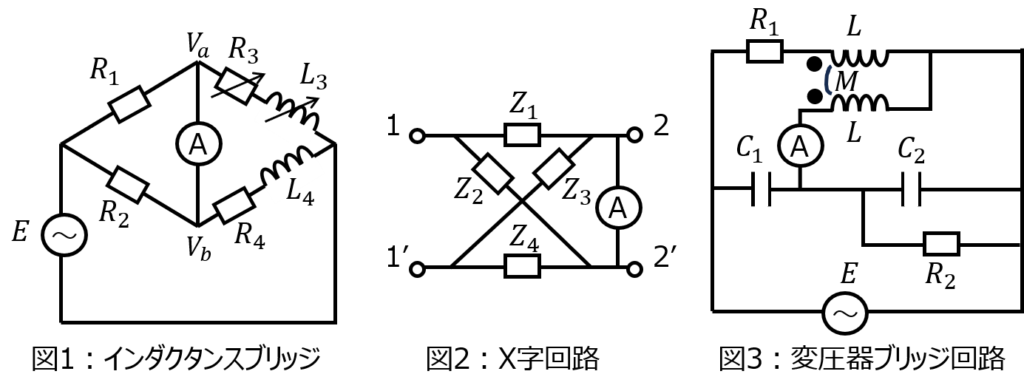
(1)図1:\(R_{1}=2k\Omega,R_{2}=4k\Omega,R_{3}=1k\Omega,L_{3}=20mH\)のインダクタンスブリッジ回路において、\(R_{4},L_{4}\)を決定せよ。
(2)図2:X字の回路
(3)図3:変圧器が含まれたブリッジ回路
ホイートストーンブリッジとは
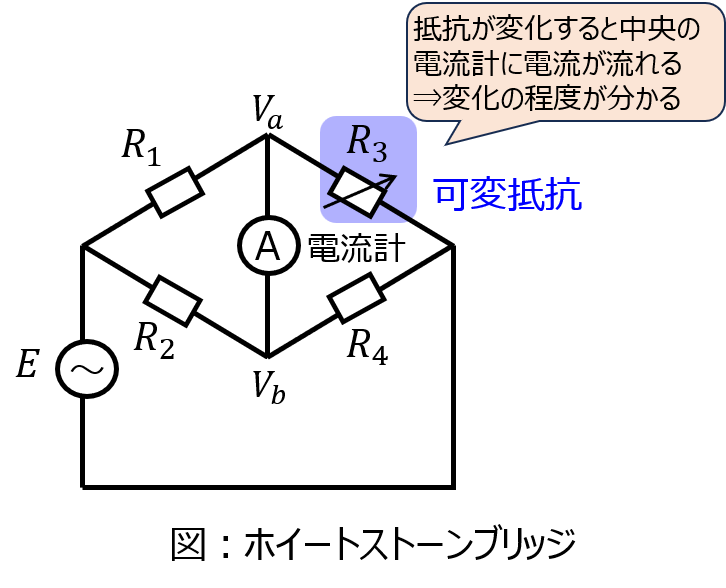
主にセンサの計測に用いられる回路になっています。電圧源(電流源)から見て導線が二手に分かれ、途中(真ん中)で繋がっている様が梯子に見えることから、このような呼ばれ方をしています。
回路には4つの抵抗(インピーダンス)が存在しており、特に外乱も無い平常状態だと真ん中の電流計に電流が流れないような設計になっています。
そのうち1つが可変抵抗となっており、計測したい物理量によって抵抗値が変化する仕掛けになっています。
計測対象の物理量が変化したとき、可変抵抗も変化することから中央の電流計に電流が流れることで、変化量を計測できます。
温度、圧力を計測したい場合の一例を下記に示します。
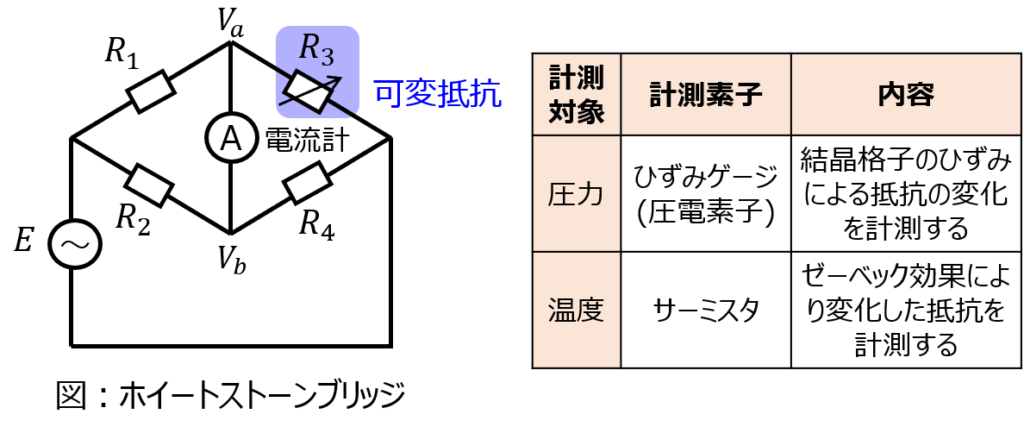
平衡条件
一例として、下記の電気回路を考えます。
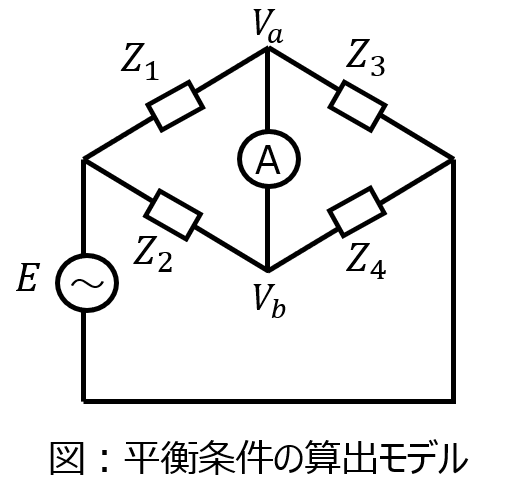
真ん中の電流計に流れない条件は、下記になります。
回路の対角線上の抵抗(インピーダンス)の積が、もう一方の対角線上の積と等しいこと
\begin{aligned}Z_{1}Z_{4}=Z_{2}Z_{3}\end{aligned}
抵抗とリアクタンスが混じるなどし、実部と虚部が混じる場合は、それぞれが等しくなる条件を求めれば良いです。
下記に簡単な証明をします。
平衡条件の証明
電流が流れないということは、節点a,bの電位が等しくなる必要がある。
それぞれの電位は、分圧の関係により
\begin{aligned}V_{a}=\dfrac{Z_{3}}{Z_{1}+Z_{3}}E \\ V_{b}=\dfrac{Z_{4}}{Z_{2}+Z_{4}}E\end{aligned}
\(V_{a}=V_{b}\)になるため、関係式を整理すると
\begin{aligned}Z_{3}(Z_{2}+Z_{4})=Z_{4}(Z_{1}+Z_{3}) \end{aligned}
\begin{aligned}Z_{1}Z_{4}=Z_{2}Z_{3}\end{aligned}
以上より、証明できた。
これは、インピーダンスが一つの素子からなる場合でなくとも適用できます。例えば、ブリッジ回路の右上の部分に抵抗\(R\)とインダクタンス\(L\)がそれぞれ1つずつ存在する場合、\(Z_{3}=R+j \omega L\)とすることで、上式を適用できます。
このように、節点間の素子を一つのインピーダンスでまとめることさえできれば、平衡条件を使用できます。
解答例
(1)インダクタンスブリッジ回路
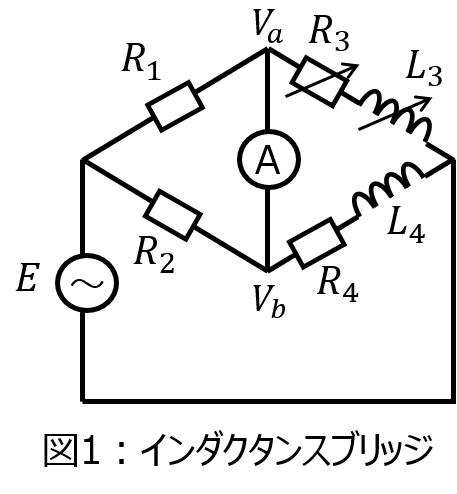
\begin{cases}Z_{1}=R_{1} \\ Z_{2}=R_{2} \\ Z_{3}=R_{3}+j \omega L_{3} \\ Z_{4}=R_{4}+j \omega L_{4}\end{cases}
(4)式に代入すると
\begin{aligned}R_{1}(R_{4}+j \omega L_{4})=R_{2}(R_{3}+j \omega L_{3}) \end{aligned}
実部と虚部同士を比較して
\begin{cases}R_{1}R_{4}=R_{2}R_{3} \\ j \omega L_{4}R_{1}=j \omega L_{3}R_{2}\end{cases}
問題で与えられたパラメータを代入すると
\begin{cases}R_{4}=\dfrac{R_{2}R_{3}}{R_{1}}=2 [kΩ] \\ L_{4}=\dfrac{L_{3}R_{2}}{R_{1}}=40 [mH]\end{cases}
(2)X字の回路
この形、実はブリッジ型回路に書き直すことができます。カンの良い方なら初見で気づいたかもしれません。知識で解決できるため、是非覚えておきましょう。
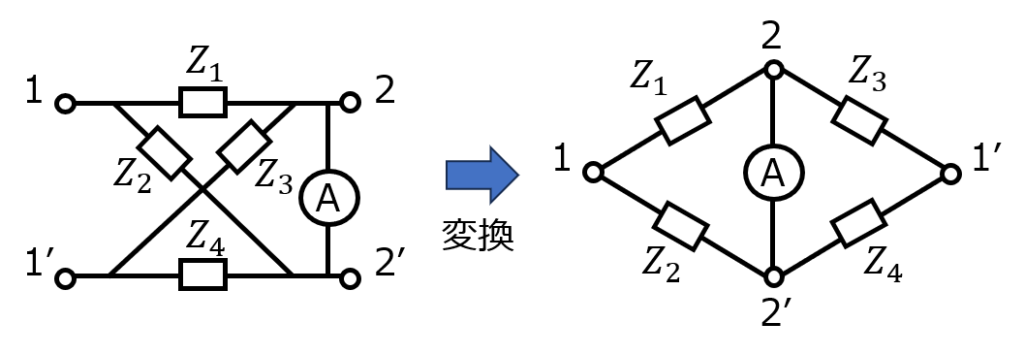
平衡条件:(1)式をそのまま適用すれば良い。
(3)変圧器が含まれたブリッジ回路
相互インダクタンスMで結合されている変圧器回路は、その部分をT型回路に変換できます。
これを用いると与えられた回路は下記のように変換できます。
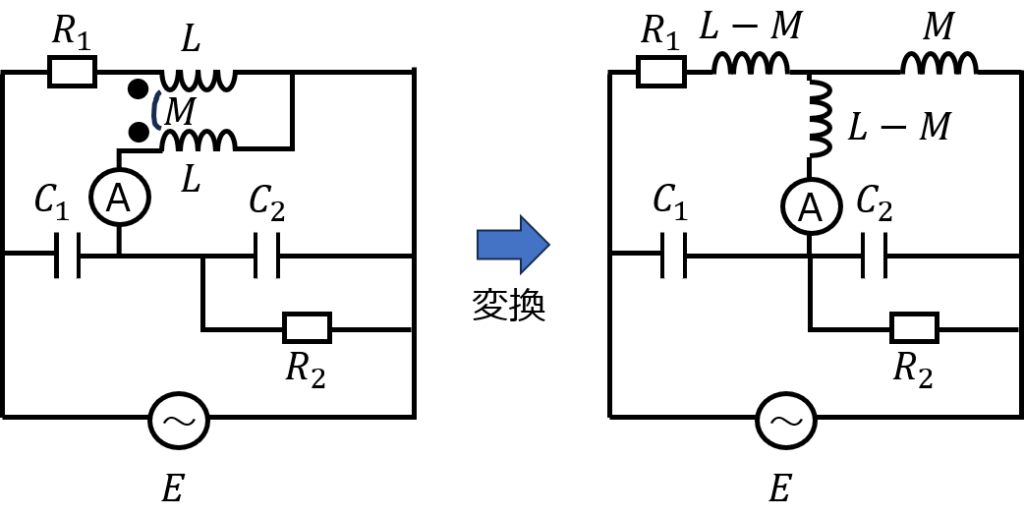
電流計の付いている枝にインダクタンス\(L-M\)が存在しますが、これは平衡条件の算出に際して無視して問題無いです。平衡条件=電流計に電流が流れない物理事象を指しているため、インダクタンスにも電流は流れないからです。
(1)と同じように、\(Z_{1},Z_{2},Z_{3},Z_{4}\)を考えます。
\begin{cases}Z_{1}=R_{1}+j \omega(L-M) \\ Z_{2}=\dfrac{1}{j \omega C_{1}} \\ Z_{3}=j \omega M \\ Z_{4}=\dfrac{R_{2}}{1+ j \omega C_{2}R_{2}}\end{cases}
これを平衡条件に代入すると
\begin{aligned}\lbrace R_{1}+j \omega(L-M) \rbrace \dfrac{R_{2}}{1+j \omega R_{2}C_{2}}=\dfrac{j \omega M}{j \omega C_{1}}\end{aligned}
\begin{aligned}-\omega^{2}C_{1}R_{2}(L-M)+j \omega C_{1}R_{1}R_{2}=-\omega^{2} M R_{2}C_{2}+j \omega M\end{aligned}
実部と虚部を比較して
\begin{cases}-\omega^{2}C_{1}R_{2}(L-M)=-\omega^{2}MR_{2}C_{2} \\\omega C_{1}R_{1}R_{2}=\omega M\end{cases}
\begin{cases}C(L-M)=C_{2}M \\ M=C_{1}R_{1}R_{2}\end{cases}
最後に
本問は、様々な大学の院試でよく出題されます。
平衡条件は、一応導出過程を解答欄に書いてから使用した方が良いかもしれません。