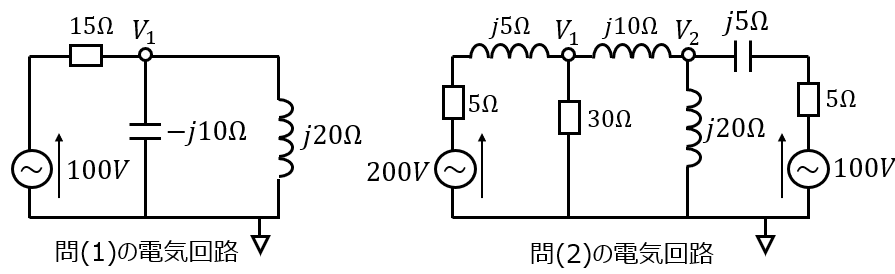
(1)下記の電気回路1の各枝に流れる電流を節点電位法を用いて求めよ。
(2)下記の電気回路2の電位\(V_{1},V_{2}\)を節点電位法を用いて求めよ。
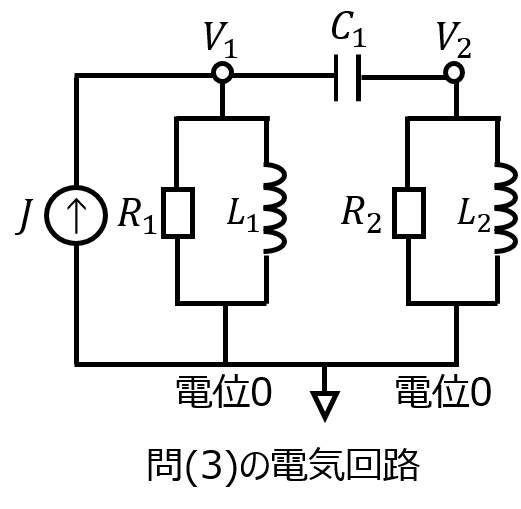
(3)下記の回路方程式で示された電気回路を図示せよ。
\begin{cases}J=\left(j \omega C_{1}+\dfrac{1}{R_{1}}+\dfrac{1}{j \omega L_{1}}\right)V_{1}-j \omega C_{1} V_{2} \\ 0=-j \omega C_{1} V_{1}+\left(j \omega C_{1}+\dfrac{1}{j \omega L_{2}}+\dfrac{1}{R_{2}}\right)V_{2}\end{cases}
節点電位法とは
回路上の節点電位を未知数として回路方程式を立てる方法を言います。
一般的に、回路方程式は、回路の各枝に流れる電流を未知数として立てることが多いです。(枝電流法と言います。)
しかし、回路の枝が多くなると電流変数の数が多くなり、計算に手間がかかってしまいます。節点を電位とする場合、回路によっては変数の数が少なくなる利点があります。
節点方程式の立て方
枝電流法では、電流\(I\)が未知数だったため、定数で表されるインピーダンスと合わせ
\begin{aligned}(電圧)=(電流)*(インピーダンス)\end{aligned}
の形で立式することが多いです。
一方で、節点電位法の場合は、電圧が未知数です。そのため、右辺に電圧を写して方程式を立てる必要があり
\begin{aligned}(電流)=(電圧)*(アドミタンス)\end{aligned}
の形で立式します。
観点としては、キルヒホッフの電流則を用います。ある節点における電流の入出力の関係を電位差で表現する。という立式の仕方となります。
慣れない形ですが、実際に例題を解いてみることで体感してみましょう。
解答例
(1)の解答例
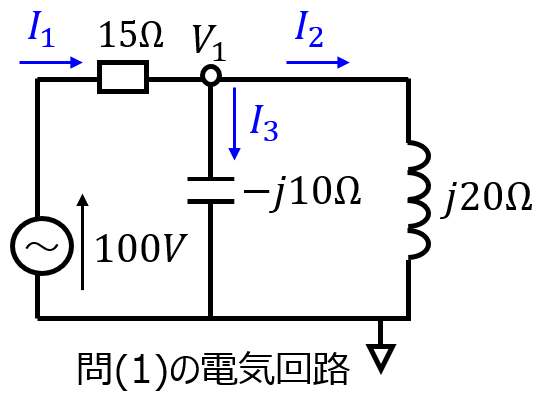
電位\(V_{1}\)を持つ節点1に注目する。電流ベクトル\(I_{1},I_{2},I_{3}\)が図の向きに出ているとすると、節点方程式は
\begin{cases}V_{1}=100-15I_{1} \\ V_{1}=j20I_{2} \\ V_{1}=-j10I_{3}\end{cases}
それぞれ、電流\(I_{i}\)に関して変形すると
\begin{cases}I_{1}=\dfrac{100-V_{1}}{15} \\ I_{2}=\dfrac{V_{1}}{j20} \\ I_{3}=-\dfrac{V_{a}}{j10}\end{cases}
\(I_{1}=I_{2}+I_{3}\)より
\begin{aligned}\dfrac{100-V_{1}}{15}=\dfrac{V_{1}}{j20}-\dfrac{V_{a}}{j10}\end{aligned}
これを解いて、求める電位\(V_{1}\)は
\begin{aligned}V_{1}&=\dfrac{400}{4+j3} \\ &=64-j48\end{aligned}
(2)の解答例
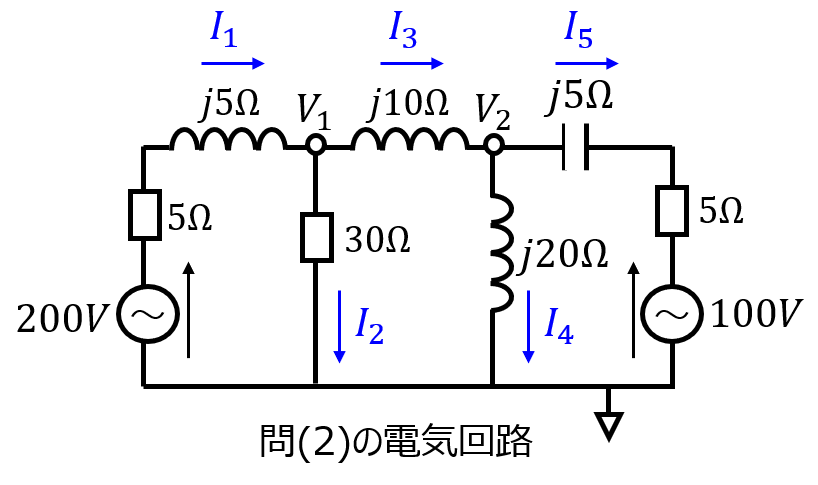
(1)に対し複雑な系ですが、電流ベクトルを電位で表し、解くことに変わり有りません。
まず、節点1にかかる電位\(V_{1}\)について
\begin{cases}200-V_{1}=(5+j5)I_{1} \\ V_{1}=30I_{2} \\ V_{1}-V_{2}=j10I_{3} \end{cases}
次に、節点2にかかる電位\(V_{2}\)について
\begin{cases}V_{2}=j20I_{4} \\ V_{2}-100=(5-j5)I_{5}\end{cases}
以上の式を、\(I_{1}=I_{2}+I_{3},I_{3}=I_{4}+I_{5}\)に代入する。
\begin{cases}\dfrac{200-V_{1}}{5+j5}=\dfrac{V_{1}}{30}+\dfrac{V_{1}-V_{2}}{j10} \\ \dfrac{V_{1}-V_{2}}{j10}=\dfrac{V_{2}}{j20}+\dfrac{V_{2}-100}{5-j5}\end{cases}
これを整理すると
\begin{cases}\left(\dfrac{1}{5+j5}+\dfrac{1}{30}+\dfrac{1}{j10}\right)V_{1}-\dfrac{1}{j10}V_{2}=\dfrac{200}{5+j5} \\ -\dfrac{1}{j10}V_{1}+\left(\dfrac{1}{j10}+\dfrac{1}{j20}+\dfrac{1}{5-j5}\right)V_{2}=\dfrac{100}{5-j5}\end{cases}
\begin{cases}\left(\dfrac{2}{15}-j\dfrac{1}{5}\right)V_{1}+j\dfrac{1}{10}V_{2}=4(5-j5) \\ j\dfrac{1}{10}V_{1}+\left(\dfrac{1}{10}-j\dfrac{1}{20}\right)V_{2}=2(5+j5)\end{cases}
\(V_{1},V_{2}\)に係数にかかる行列をAとすると、行列式は
\begin{aligned}|A|&=\begin{vmatrix} \dfrac{2}{15}-j\dfrac{1}{5} & j\dfrac{1}{10} \\ j\dfrac{1}{10} & \dfrac{1}{10}-j\dfrac{1}{20} \end{vmatrix} \\ &=\left(\dfrac{2}{15}-j\dfrac{1}{5}\right)\left(\dfrac{1}{10}-j\dfrac{1}{20}\right)-\left(j\dfrac{1}{10}\right)^{2} \\ &=\dfrac{2-j4}{150} \end{aligned}
これより、求める電位\(V_{1},V_{2}\)は
\begin{aligned}V_{1}&=\dfrac{\begin{vmatrix}4(5-j5) & j\dfrac{1}{10} \\ 2(5+j5) & \dfrac{1}{10}-j\dfrac{1}{20}\end{vmatrix}}{|A|} \\ &=150\end{aligned}
\begin{aligned}V_{2}&=\dfrac{\begin{vmatrix}& \dfrac{2}{15}-j\dfrac{1}{5} & 4(5-j5) \\ & j\dfrac{1}{10} & 2(5+j5) \end{vmatrix}}{|A|} \\ &=100\end{aligned}
(3)回路の図示
与えられた式(1)を変形すると、下記のようになる。
\begin{cases}J=\left(\dfrac{1}{R_{1}}+\dfrac{1}{j \omega L_{1}} \right)(V_{1}-0)+j \omega C_{1}(V_{1}-V_{2}) \\ 0=j \omega C_{1}(V_{2}-V_{1})+\left(\dfrac{1}{R_{1}}+\dfrac{1}{j \omega L_{1}} \right)(V_{2}-0)\end{cases}
第一式において、電位\(V_{1}\)を持つ節点1で入出力する電流の合計はJである。よって、電流源Jが接続されていることが分かる。
また、節点1とアースの間には、抵抗\(R_{1}\)とコイル\(L_{1}\)の並列回路が存在することが分かる。
また、電位\(V_{2}\)を持つ節点2との間には、コンデンサ\(C_{1}\)が存在することが分かる。
次に第二式を調べる。同じく、節点1との間にコンデンサ\(C_{1}\)が存在することがこちらの式でも分かった。
また、節点2とアースの間には抵抗\(R_{2}\)とコイル\(L_{2}\)の並列回路が存在することが分かる。
以上を踏まえると、下記の回路になることが分かる。