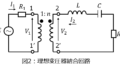下記の電気回路(1)(2)のベクトル軌跡を求めよ。
(1)コイルLを直列に繋ぎ、RCを並列に繋いだ回路を考える。Lの大きさを変化させたとき、端子1-1’から回路に流れる電流\(I_{L}\)の変化をベクトル軌跡で表せ。
(2)RLを並列に接続したブリッジ回路において、Rが0から∞に変化したときを考える。端子ab間の電圧\(V_{ab}\)のベクトル軌跡を求めよ。
ベクトル軌跡とは
回路の特性を複素平面上にプロットした線図を言います。(円線図とも言います。)
冒頭で与えた問題のように、変化させるパラメータを変数に取り軌跡を描くことで、そのときの回路の特性を視覚的に把握できます。
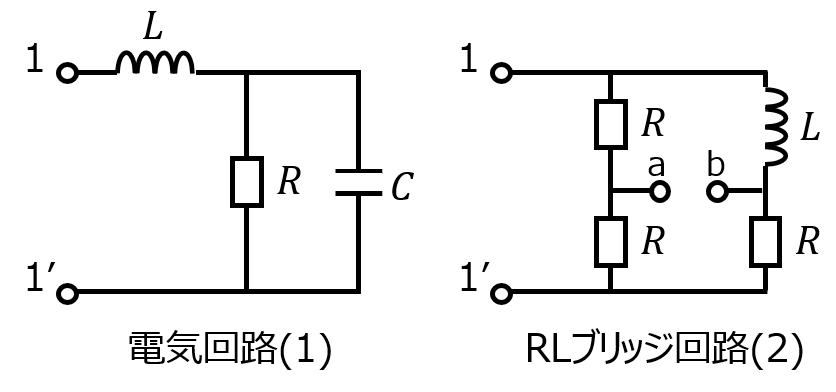
例えば、あるインピーダンス\(Z\)の軌跡は下記の図1で表されるとします。下記のような解釈ができます。
- \(\omega=\omega_{1}\)のときは虚部成分が負に大きくなることから、容量性負荷を持つ。
- \(\omega=\omega_{2}\)のときは虚部が0であることから共振周波数である。
- \(\omega=\omega_{3}\)のときは虚部成分が正に大きくなることから、誘導性負荷を持つ。
これは、周波数によって回路の特性を変えたいときに有用です。
円線図の作図方法
下記の視点で図を書くと、うまく行きやすいです。
- 作図対象が分数表記のとき:分子、分母それぞれの作図をし、両者を重ね合わせる。
- 複雑な電気回路のとき:素子ごとの軌跡を考えていき、重ね合わせた結果を全体の軌跡とする。
作図方法1.の説明
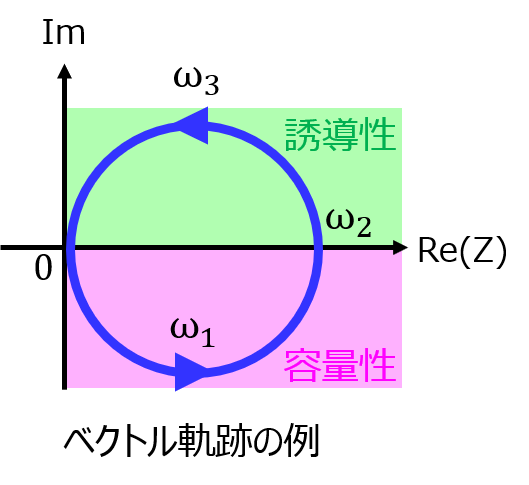
例えば、RC並列回路におけるインピーダンス
\begin{aligned}Z=\dfrac{R}{1+j \omega CR}\end{aligned}
について、\(\omega\)を0から∞に変化した場合の軌跡を考えます。
まず、分母\(1+j \omega CR\)について、角周波数を動かした時、虚部のみ影響を受けます。よって、複素平面上では実軸=Rを上下に移動する直線になります。
これを逆数にするとどうなるでしょうか。位相が逆転し、\(\omega=\dfrac{1}{CR}\)のとき、実部と虚部が一致することから、下向きの半円となります。
あとは、分子\(R\)の影響を加味すればベクトル線図の完成です。上記の軌跡をR倍すれば良いわけですから
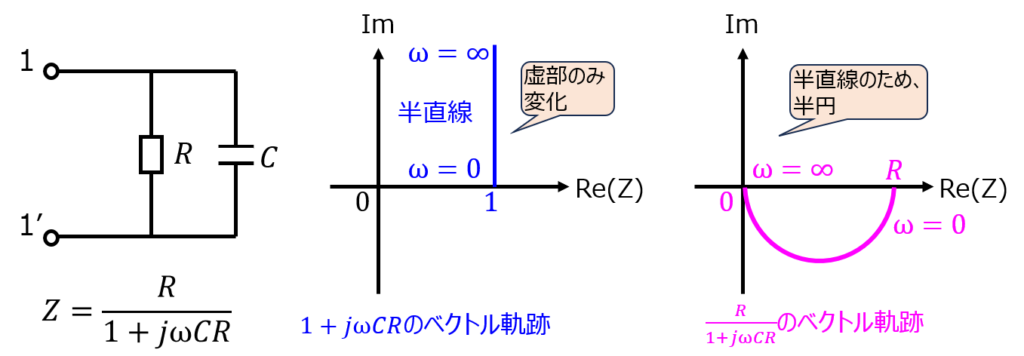
になります。全体の式を構成する要素を一つ一つ考えていくことで、作図することができました。
ある実軸を上下に移動する軌跡は、逆数にすると円になる事実は覚えておくと有用です。
作図方法2.の説明
下記の電気回路のインピーダンスの軌跡を考えます。抵抗\(R_{o}\)に対し、RLC並列回路が直列で接続されています。\(\omega\)を変数とします。
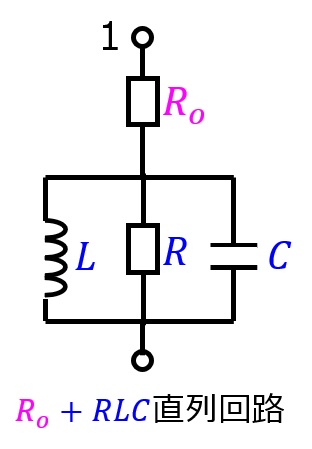
この場合、\(R_{o}\)の軌跡とRLC並列回路の軌跡の重ね合わせが求めるベクトル軌跡になります。
まず、\(R_{o}\)のベクトル軌跡について、角周波数を持たないことから実軸\(R_{o}\)の固定点となります。
次にRLC並列回路のベクトル軌跡を考えます。インピーダンスは
\begin{aligned}Z=\dfrac{1}{R+j\left(\omega L – \dfrac{1}{\omega C} \right)}\end{aligned}
であり、\(\omega=0\)のときは、コンデンサ成分が無限大となるので、複素平面上の原点(0,0)に当たります。
そこから、\(\omega\)を増加させたとき、分母のコンデンサ成分は変わらずコイル成分より強いです。通分した分母の虚部\(j \omega CR\)が正で、有理化すると分子は負になることから、ベクトル線図の虚部は負の領域に移動します。
やがて、コンデンサ成分とコイル成分が等しくなり、共振周波数を迎えると、今度はコイルの成分が強くなります。よって、ベクトル線図の虚部は負の領域に突入します。
角周波数を∞とすると、コイル成分が無限大となるので、\(\omega=0\)のときと同じく複素平面上の原点(0,0)に当たります。
上記を総合すると、RLC並列回路の軌跡は時計回りの円になることが分かります。
これを\(R_{o}\)の軌跡と合成すれば良いです。実軸を\(R_{o}\)分オフセットさせれば良いので
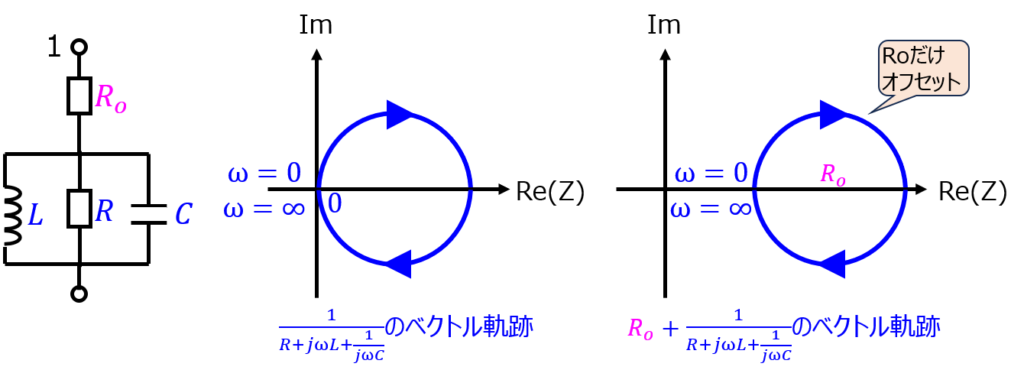
となります。合成インピーダンスとして一度に考えると式変形が複雑になりがちですが、楽に作図することができました。
解答例
(1)
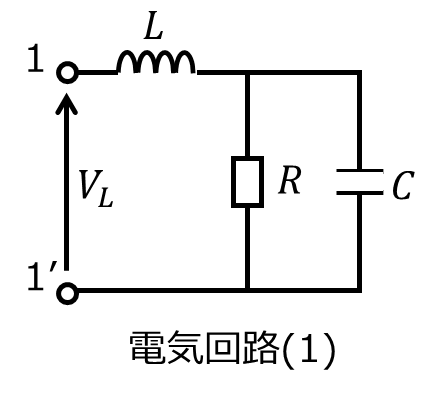
作図方法1.を用いて解きます。
端子1-1’間の電圧を\(V_{L}\)とすると、回路に流れる電流は
\begin{aligned}I_{L}&=\dfrac{V_{L}}{j \omega L+\dfrac{R}{1+j \omega CR}} \\ &=\dfrac{V_{L}}{\dfrac{R}{1+(\omega CR)^{2}}+j \left(\omega L -\dfrac{\omega CR^{2}}{1+(\omega CR)^{2}}\right)}\end{aligned}
まず分母\(\dfrac{R}{1+(\omega CR)^{2}}+j \left(\omega L -\dfrac{\omega CR^{2}}{1+(\omega CR)^{2}}\right)\)の軌跡について、Lが変数なので、実軸\(\dfrac{R}{1+(\omega CR)^{2}}\)を上下に移動する軌跡となる。
これを逆数にすると円線図になる。結果を分子の\(V_{i}\)倍することに注意すると、求める軌跡は
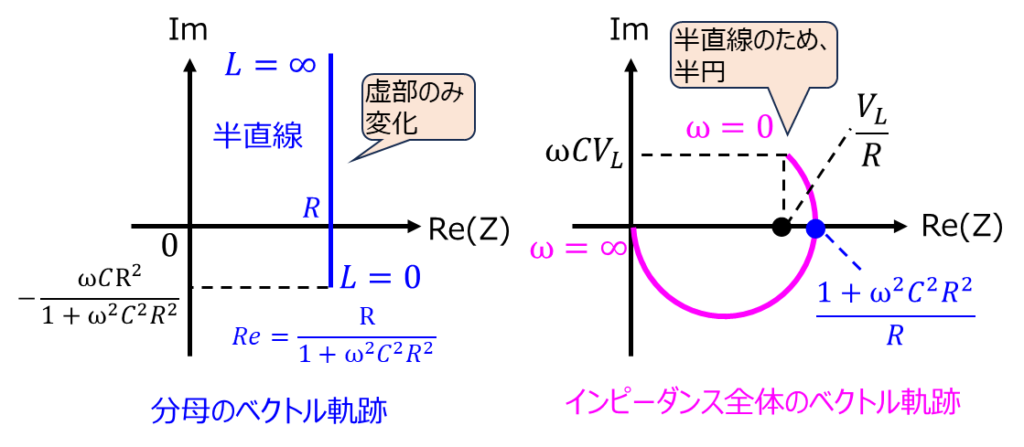
(2)
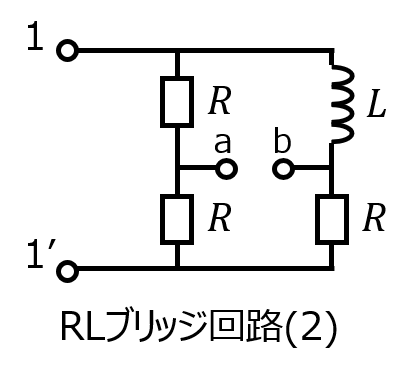
端子ab間の電圧\(V_{ab}\)は、分圧の法則により
\begin{aligned}V_{ab}&=\left(\dfrac{R}{R+j \omega L} -\dfrac{1}{2}\right)E \\ &=\left(\dfrac{1}{1+j \omega L/R} -\dfrac{1}{2}\right)E\end{aligned}
上式に対し、(i)Rが変化する場合を考える。
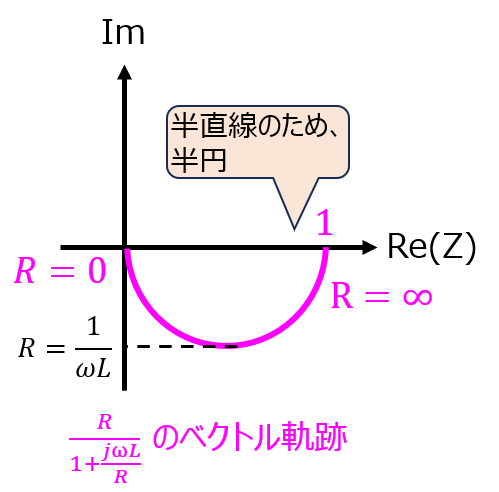
\(1+\dfrac{\omega L}{R}\)において、実軸1を虚軸の正の領域に移動する半直線になることから
逆数として考えると、半円になる。位相が逆になるので、下向きの半円になる。
(4)式により、上記の結果に対し実軸を-E/2分オフセットさせれば良いので、求める軌跡は
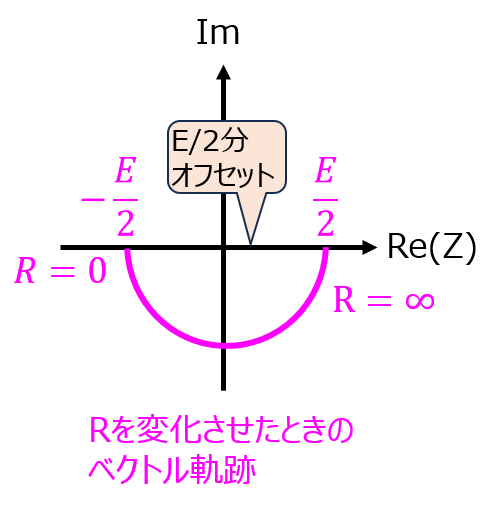
原点を中心とする下向きの半径E/2の半円であることが分かった。
最後に
ベクトル軌跡は、一部の大学の院試でよく出題されます。
自身の受けようとしている大学の過去問で出題されている場合は、是非対策しましょう。