長さが\(l\)、半径がa、巻き数がNのソレノイドコイルが有る。このソレノイド内の中心部に半径が\(b\)の円形コイル(巻き数1)が中心軸に対し\(\theta\)をなす角で存在する。\(a<<l\)とし、ソレノイドコイル内の磁場は一定とみなせる無限長ソレノイドコイルである仮定で下記の問いに答えよ。なお、透磁率は\(\mu_{o}\)とする。
(1)ソレノイドコイルに電流\(I\)を流した時、ソレノイド内の磁場\(H\)と自己インダクタンス\(L\)を求めよ。
(2)ソレノイドコイルと円形コイルの相互インダクタンスを求めよ。また、(1)の条件で円形コイルに発生する回転軸方向のトルクはいくらか。
(3)ソレノイドに電流\(I\)を流し、円形コイルを\(\omega\)で回転させる。このとき、円形コイルに発生する誘導起電力\(V_{3}\)を求めよ。
(4)ソレノイドに交流電流\(I\cos\theta_{2}t\)を流し、円形コイルを角速度\(\theta\)で回転させるとき、円形コイルに発生する誘導起電力\(V_{4}\)を求めよ。
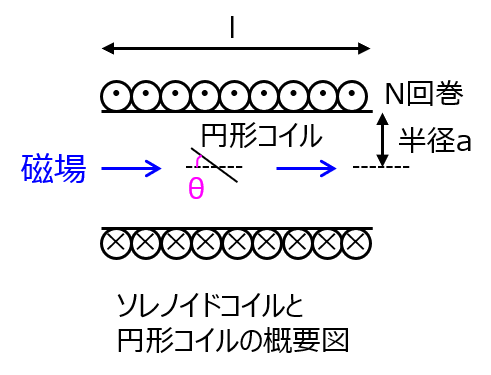
ソレノイドコイルとは
導線を円筒状に巻いたコイルです。一つ一つの巻き線に対し中心軸上に磁場が発生します。何回も巻くことで、強い磁場が出せるようになり、モータなど様々な電気機器に使用されています。
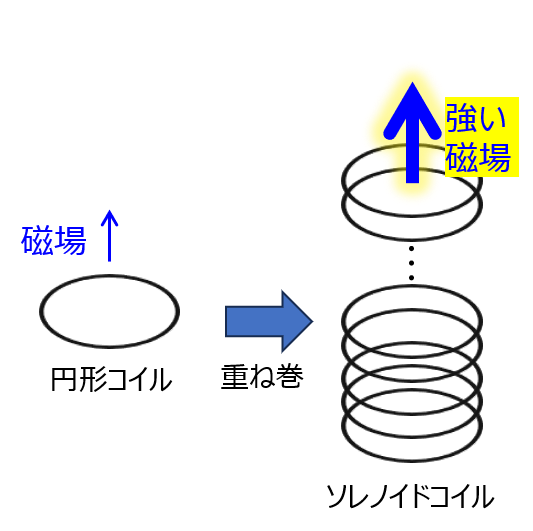
有限長ソレノイドコイル内の磁場分布
1回巻の円形コイルから発生する磁場の重ね合わせで考えます。
以前の記事より、半径aの円形コイルの中心軸上の位置zで発生する磁場は下記で表されます。
\begin{aligned}H=\dfrac{Ia^{2}}{2(a^{2}+z^{2})^{3/2}}\end{aligned}
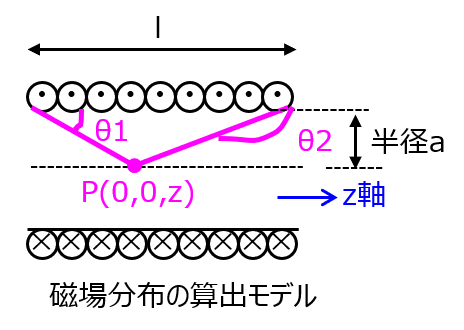
中心軸上の点P(0,0,z)から有限長ソレノイドの左右の端面を見た角度を\(\theta_{1},\theta_{2}\)、\(r=\sqrt{a^{2}+z^{2}}\)とすると
\begin{aligned}dH&=\dfrac{Ia^{2}}{2(a^{2}+z^{2})^{3/2}}dz \\ &=\dfrac{nI\sin^{2}\theta}{2r}dz \\ &=-\dfrac{nI}{2}\sin \theta d \theta\end{aligned}
なお、積分の変数変換には、\(z=a \cot\theta,dz=-\frac{a}{\sin^{2} \theta}d\theta=-\frac{r}{\sin \theta}d\theta,a=r\sin \theta\)を用いている。
また\(n\)は、単位長さあたりの巻き数\(n=N/l\)である。
上式を、\(\theta_{1},\theta_{2}\)の範囲で積分すると
\begin{aligned}H&=-\dfrac{nI}{2}\int^{\theta_{2}}_{\theta_{1}}\sin \theta d\theta \\ &=\dfrac{nI}{2}(\cos\theta_{2}-\cos \theta_{1})\end{aligned}
無限長ソレノイド内の磁場分布
有限長ソレノイドの極限で求める方法
これは、前節の計算結果を利用することで解けます。
無限長ソレノイドになるときは、\(\theta_{1}=-\pi,\theta_{2}=0\)になるので
\begin{aligned}H=nI=NI/l\end{aligned}になります。
なお、この解法は計算量が多いです。(ネガポイント)
前節のように座標系を置くことを工夫し、三角関数の積分が必要です。一方で、アンペールの法則を用いるときは、長方形の線積分で済むため、簡潔な計算で解くことができます。
アンペールの法則を用いる方法
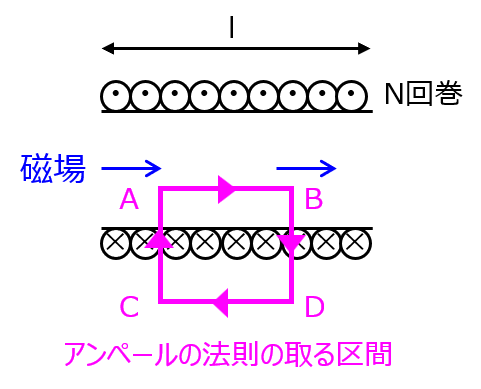
一辺ABがソレノイドコイル内で磁場が発生している領域をまたぐ閉曲線ABCDを考える。
ABの長さをaとし、アンペールの法則を適用すると、下記のように分解できる。
\begin{aligned}\int_{AB+BC+CD+DA}\boldsymbol{H} ・ d\boldsymbol{s} = \int_{AB}\boldsymbol{H}・ d\boldsymbol{s}-\int_{CD}\boldsymbol{H}・ d\boldsymbol{s} \end{aligned}
\begin{aligned}Ha=nIa \\ H=nI \\ H=NI/l \end{aligned}
このように、無限長ソレノイド(または長さが十分に長い有限長ソレノイド)の場合、前節のように極限を考えなくても、アンペールの法則を利用して中心軸上の磁場を求めることができます。
円形コイルに作用するトルク
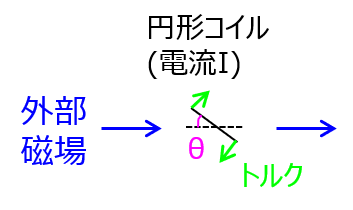
下記のように、一定の電流\(I\)が流れている面積\(S\)の円形コイルに対し、外部磁場が作用する系を考える。
磁場\(H\)に対して\(\theta\)の角度をコイルがなしている時の仕事を考える。トルクを\(T\)とし、鎖交磁束が\(\phi\)のとき、回路の持つ位置エネルギーは
\begin{aligned}U=-I\phi\end{aligned}
になります。これを変数\(\theta\)で微分すると、回転軸方向にかかる力(トルク)を求めることができ
\begin{aligned}T&=I\dfrac{\partial \phi}{\partial \theta} \\ &= II_{out}\dfrac{\partial M}{\partial t}\end{aligned}
\(M\)は外部磁界を発生させるコイルと円形コイルの相互インダクタンスです。また、\(I_{out}\)は、外部磁界を発生させるコイルに流れる電流です。(問題文では、ソレノイドコイルに流す電流が該当します。)
以上より、円形コイルを貫く磁束が求まれば、これを\(\theta\)で微分することによりトルクが求められることが分かりました。(3)で使います。
解答例
(1)ソレノイド上の磁場
前節までの説明により
\begin{aligned}H=\dfrac{NI}{l}\end{aligned}
(2)トルクの大きさ
円形コイルに鎖交する磁束\(\Phi_{2}\)は
\begin{aligned}\Phi_{2}=\dfrac{\mu_{o}NI}{l}\pi b^{2}\cos \theta\end{aligned}
これより、相互インダクタンス\(M\)は
\begin{aligned}M=\dfrac{\mu_{o} \pi N}{l}b^{2} \cos \theta\end{aligned}
これより、求めるトルクの大きさは
\begin{aligned}T&=\left|\dfrac{\partial \Phi_{2}}{\partial \theta}I\right| \\ &=\left|\dfrac{\partial M}{\partial \theta}I^{2}\right| \\ &=\dfrac{\mu_{o}\pi N}{l}b^{2}I^{2} \sin \theta \end{aligned}
(3)円形コイルを回転させたときの誘導起電力
このときの鎖交磁束\(\Phi_{3}\)は
\begin{aligned}\Phi_{3}=\dfrac{\mu_{o}NI}{l}\pi b^{2}\cos \theta t\end{aligned}
電磁誘導の法則より、求める誘導起電力は
\begin{aligned}V_{3}=-\dfrac{\partial \Phi_{3}}{\partial t}=\dfrac{\mu_{o}NI\omega}{l}\pi b^{2}\sin \theta t \end{aligned}
(4)交流電流を流した時の誘導起電力
このときの鎖交磁束\(\Phi_{4}\)は
\begin{aligned}\Phi_{4}=\dfrac{\mu_{o}NI}{l}\pi b^{2}\cos \theta t \cos \theta_{2}t \end{aligned}
電磁誘導の法則より、求める誘導起電力は
\begin{aligned}V_{4}=-\dfrac{\partial \Phi_{4}}{\partial t}=\dfrac{\mu_{o}NI\omega}{l}\pi b^{2}(\omega \sin \theta t \cos \theta_{2}t+ \omega_{2}\cos \theta t \sin \theta_{2} t) \end{aligned}