下記の2つの磁性体を考える。それぞれの問いに答えよ。なお、漏れ磁束に関しては無視できるとする。
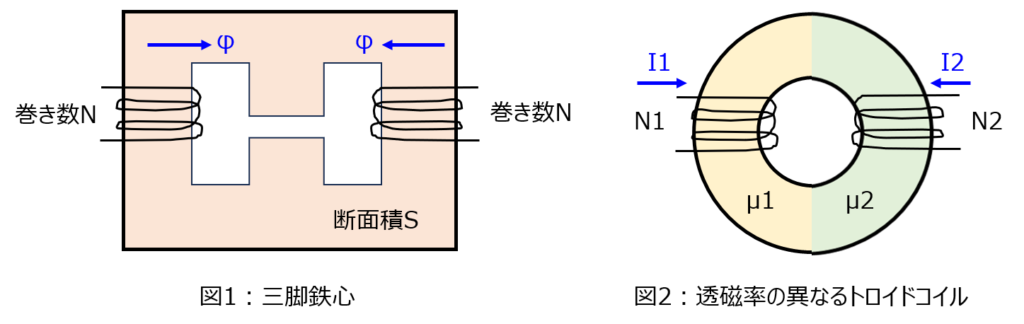
(1)図1のように、断面積Sの三脚鉄心を考える。左右の鉄心は、両方N回巻きのコイルで上向きに励磁している。このとき、中央の脚の空隙\(\delta\)における磁場を求めよ。
(2)図2に示すように、左半分が透磁率\(\mu_{1}\),右半分が\(\mu_{2}\)の環状トロイドを考える。左半分には、巻き数\(N_{1}\)の銅線、右半分には巻き数\(N_{2}\)の銅線が巻かれ、それぞれ上向き、下向きの磁場が発生するように電流を流す。
(2-a)コイル2に電流を流さない時、トロイドコイルの磁性体1、磁性体2内部の磁場\(H_{1},H_{2}\)、磁束密度\(B_{1},B_{2}\)を求めよ。
(2-b)コイル1とコイル2間の相互インダクタンス\(M\)を求めよ。
(2-c)コイル2の自己インダクタンス\(L_{2}\)を求めよ。
磁気回路法とは
磁束の流れを回路モデルに置換し、これを解くことにより、磁場などのパラメータを求める手法です。
アンペールの法則を用いて磁性体内部の磁場を求める方法もありますが、こちらの方法では回路として機械的に計算するため、システマティックに特性を求められる利点があります。
回路パラメータの置き方
電気回路での基本パラメータは、電圧\(V\)、電流\(I\)、抵抗\(R\)でした。磁気回路では、それぞれ下記に置き換えます。
- 電圧\(V\)→起磁力\(NI\)
- 電流\(I\)→磁束\(\Phi\)
- 抵抗\(R\)→磁気抵抗\(\dfrac{1}{\mu S}\)
磁気回路のため、電流に関しては磁束にそのまま変数を置き換えれば良いです。
抵抗に関して、電気回路では\(R=\dfrac{l}{\sigma S}\)でした。導電率を透磁率に置き換えれば良いです。
電圧に関しては、アンペールの法則により
\begin{aligned}\int_{c}\boldsymbol{H}・d\boldsymbol{s}=Hl=NI\end{aligned}
なので、上記の書き換えができます。
解答例
(1)三脚鉄心の空隙部における磁場
与えられた鉄心は、下記のような磁気回路モデルに置き換えられる。
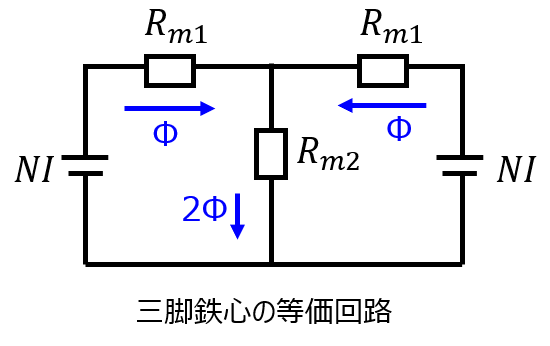
\begin{cases}V_{m}=NI \\ R_{m1}=\dfrac{3l}{\mu S} \\ R_{m2}=\dfrac{l-\delta}{\mu S}+\dfrac{\delta}{\mu_{o}S} \\ V_{m}=R_{m1}\Phi+2R_{m2}\Phi \end{cases}
これを解くと
\begin{aligned}\Phi&=\dfrac{V_{m}}{R_{m1}+R_{m2}} \\ &=\dfrac{NI \mu \mu_{o}S}{(5l-2\delta)\mu_{o}+2\delta \mu}\end{aligned}
\( \Phi = BS=\mu_{o}HS\)より、空隙内の磁場\(H\)は
\begin{aligned}H=\dfrac{2 \Phi}{\mu_{o} S}=\dfrac{2NI \mu}{(5l-2\delta)\mu_{o}+2\delta \mu}\end{aligned}
(2)左右で透磁率の異なる円環トロイド
(a)磁性体1,2内部の磁場\(H\)、磁束密度\(B\)
与えられたトロイドコイルは、下記のような回路モデルに置き換えられる。
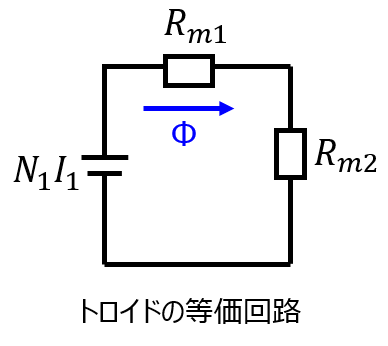
\begin{cases}V_{m}=N_{1}I_{1} \\ R_{m1}=\dfrac{\pi a}{\mu_{1}S} \\ R_{m2}=\dfrac{\pi a}{\mu_{2}S} \\ V_{m}=R_{m1}\Phi+R_{m2}\Phi\end{cases}
これを解いて、磁束\(\Phi\)は
\begin{aligned}\Phi=\dfrac{\mu_{1}\mu_{2}SN_{1}I_{1}}{\pi a (\mu_{1}+\mu_{2})}\end{aligned}
次に、磁束密度\(B\)は、境界面に対して連続なので、磁性体1,2共通して
\begin{aligned}B=\dfrac{\Phi}{S}=\dfrac{\mu_{1}\mu_{2}N_{1}I_{1}}{\pi a (\mu_{1}+\mu_{2})}\end{aligned}
最後に、磁場について\(H_{1}=\mu_{1}B,H_{2}=\mu_{2}B\)だから
\begin{cases}H_{1}=\dfrac{\mu_{2}N_{1}I_{1}}{\pi a (\mu_{1}+\mu_{2})} \\ H_{2}=\dfrac{\mu_{1}N_{1}I_{1}}{\pi a (\mu_{1}+\mu_{2})}\end{cases}
(b)コイル1,2間の相互インダクタンス
\(\Phi_{2}=MI_{1}\)の関係により、相互インダクタンスを求める。
コイル2を貫く鎖交磁束を求めるためには、コイル1から発生する磁束をまず考える必要がある。\(\Phi_{2}=N_{2}\phi_{1}\)であり、\(\phi_{1}\)は(6)式を用いれば良いので
\begin{aligned}\Phi_{2}=\dfrac{\mu_{1}\mu_{2}N_{1}N_{2}I_{1}}{\pi a (\mu_{1}+\mu_{2})} \\ M=\dfrac{\mu_{1}\mu_{2}N_{1}N_{2}}{\pi a (\mu_{1}+\mu_{2})}\end{aligned}
(c)コイル2の自己インダクタンス
コイル2から発生した磁束\(\phi_{2}\)がコイル2自身を貫くときの鎖交磁束\( \Phi_{2}\)を利用し、\(\Phi_{2}=L_{2}I_{2}\)の関係を用いて解けば良い。
\(\phi_{2}\)は、(6)式の\(I_{1}\)を\(I_{2}\)に置き換えれば良く
\begin{aligned}\phi_{2}=\dfrac{\mu_{1}\mu_{2}N_{2}I_{2}}{\pi a (\mu_{1}+\mu_{2})}\end{aligned}
これより、鎖交磁束\( \Phi_{2} =N_{2}\phi_{2}\)と自己インダクタンス\(L_{2}\)は
\begin{cases}\Phi_{2}=\dfrac{\mu_{1}\mu_{2}N_{2}^{2}I_{2}}{\pi a (\mu_{1}+\mu_{2})} \\ L_{2}=\dfrac{\mu_{1}\mu_{2}N_{2}^{2}}{\pi a (\mu_{1}+\mu_{2})}\end{cases}
最後に
磁気回路法は、院試でそのまま出題されることは少ないですが、アンペールの法則で導き出した答えを確認する上では有用な方法です。
本問も解けるようにしておき、試験本番で迷うような答えが出た際は、本知見から妥当性を確かめられるようにしておきましょう。


