【ガウスの法則】電荷密度が変化する物体から発生する電場の算出

以下の問を考えます。

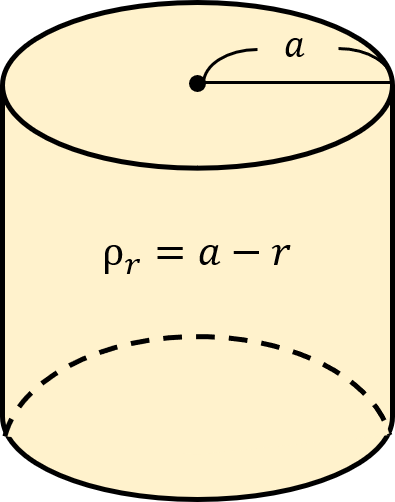
半径aの無限に長い円柱1の内に、空間電荷密度が\(\rho(r)=\left( a-r\right)\)の電荷が分布している。この円柱内外の電界\(E_{1}\) \(E_{2}\)を求めよ。但し、rは円柱中心軸からの半径を表す。

はじめに
よくある誤答例
本問を通して理解したいこと
解答例
最後に
参考文献

はじめに

上記の問題にはひっかけ要素が含まれています。電磁気学を勉強中の学部1,2年生の方々からすると、一度は引っかかる内容かもしれません。

よくある誤答例

ガウスの法則を使用し、電場を求める。

\(\int_S \mathbf{E}\cdot \mathbf{dS}=\int_V \frac{\rho}{\varepsilon_{0}}\, dV\)

半径r、高さ1の円柱型の閉曲面Sをとり、以下の場合分けを行う。

(i) r<aのとき (閉曲面が円柱1内)

電荷は、\(Q_{1}=\left( a-r\right) \pi r^{2}\)で与えられるので

求める電場\(E_{1}\)は

\begin{split}2\pi rE_{1}=\frac{Q_{1}}{\varepsilon _{0}}\end{split}

これを変形すると

\begin{split}E_{1}&=\frac{Q_{1}}{2\pi r\varepsilon _{0}}\\&=\frac{\left( a-r\right) }{2\pi r\varepsilon _{0}}\cdot \pi r^{2}\\&=\frac{r\left( a-r\right) }{2\varepsilon _{0}}\end{split}

を得る。

(ii)r>aのとき (閉曲面が円柱1外)

半径rにおける電荷は、\(Q_{2}=\left( a-a\right) \pi a^{2}=0\)で与えられ、円柱1外に電荷は存在しないことが確認できた。

このため、ガウスの法則を適用すると、円柱外で発生する電場\(E_{2}\)は0を取る。

どこが間違っているか、お気づきになられましたでしょうか。

本問を通して理解したいこと

微小区間では、変化するパラメータを一定とみなせる
一定とみなした区間を積分することで、積分対象のパラメータの総量を求められる
ガウスの法則は、自身がとった閉曲面内に存在する電荷の総量に注目する

本問は、ガウスの法則の理解を深めるだけでなく、大学で物理学を勉強していく上で必ず押さえておきたい要素があります。

上記の場合分け(i)で間違っている部分にピンと来ましたでしょうか。

正解は、電荷の総量を求める際、一定値として計算してしまっていること　でした。

誤)\begin{split}Q_{1}=\left( a-r\right) \pi r^{2}\end{split}

正)\begin{split}Q_{1}=\int ^{r}_{0}\left( a-r’\right) \cdot 2\pi r’\cdot dr’\end{split}

になります。

前者の計算では、半径r地点での電荷密度ρ(r)が0~rすべての区間に一様に分布している前提になってしまっています。

高校物理までは、パラメータが一定値であることが多く、前者の計算で問題無かったです。

しかし、大学になると、変化するパラメータを取り扱うことが多くなります。

このときは、微小円環区間 \(2\pi r\cdot dr\) に存在する電荷量\(dQ=2\pi r\cdot \rho \left( r\right) dr\)をまず考え、これを閉曲面で取った区間(0<r'<r)で積分しなければなりません。

また、誤った計算をすると、場合分け(ii)で算出した電場\(E_{2}\)は物理的につじつまの合わない値になります。

(問題では負の電荷は与えられておらず、正の電荷から発生する電場が存在するはずなのに、算出結果が0)

このとき、ガウスの法則の意味「閉曲面をSを貫く電気力線の総数は、Sの内部に存在する全電荷を\(\varepsilon _{0}\)で割った結果に等しい」ということを押さえておけば、そもそもの電荷量の算出方法に誤りがありそう。と気づくことができるはずです。

解答例

(i) r<aのとき (閉曲面が円柱1内)

閉曲面内の総電荷量は、\(Q_{1}=\int ^{r}_{0}\left( a-r’\right) \cdot 2\pi r’\cdot dr’\)で与えられるので、これを計算すると

\begin{split}Q_{1}&=2\pi \int ^{t}_{0}\left( ar’-r’^{2}\right) dr’\\&=2\pi \left[ a\cdot \frac{r’^{2}}{2}-\frac{r’^{3}}{3}\right] _{0}^{r}\\&=2\pi r^{2}\left( \frac{a}{2}-\frac{r}{3}\right)\end{split}

以上より、求める電場\(E_{1}\)は、\(2\pi rE_{1}=\frac{Q_{1}}{\varepsilon _{0}}\) から

\begin{split}E_{1}=\frac{r}{\varepsilon _{0}}\left( \frac{a}{2}-\frac{r}{3}\right)\end{split} を得る。