下記に示すように、平板の厚みがt、導体間の距離がdの平板コンデンサが存在する。導体1に電荷密度\(\sigma_{1}\)、導体2に電荷密度\(\sigma_{2}\)の電荷を与える。
このとき、下記のパラメータを求めよ。
- 導体1の左側、導体1,2の間、導体2の右側の電場\(E_{1},E_{2},E_{3}\)
- それぞれの導体の左右に誘起する電荷\(\sigma_{1L},\sigma_{1R},\sigma_{2L},\sigma_{2R}\)

ガウスの法則の意味
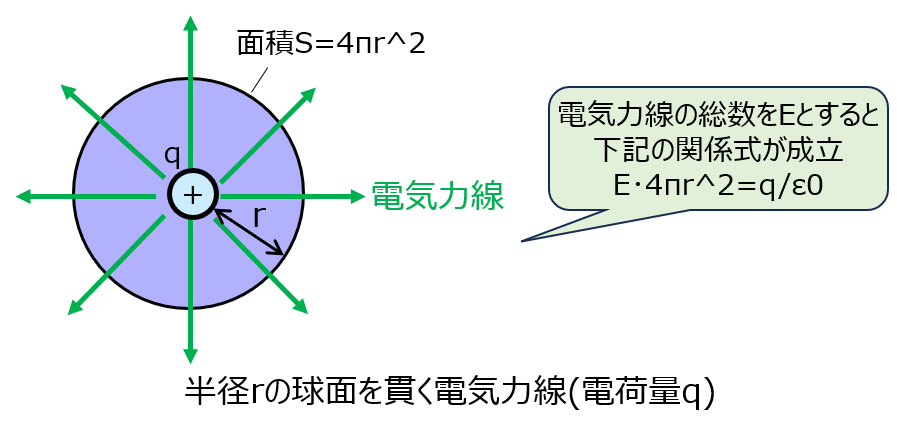
閉曲面Sを貫く電気力線の総数が、Sの内部に存在する全電荷量を\(\varepsilon_{o}\)で割ったものに等しいことを示しています。
電気力線は電場\(E\)に言い換えることができますので、結局下記の式になります。
\begin{aligned}\int_{S} \boldsymbol{E}・d\boldsymbol{S}=\dfrac{1}{\varepsilon_{o}}\int_{V} \rho dV\end{aligned}
ガウスの法則の使い方
(1)式を利用し、問題で与えられた様々な物体から発生する電場分布を求めることが多いです。
閉曲面Sの取り方には様々なパターンがありますが、代表的なものとしては下記になります。
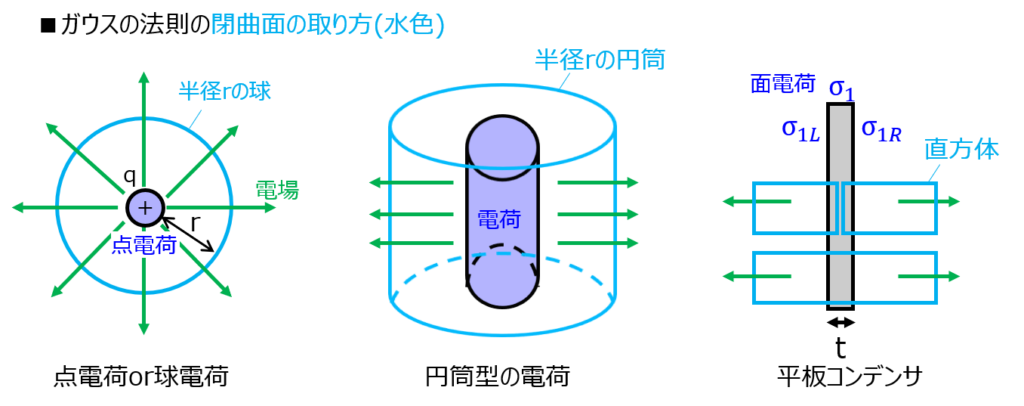
電荷分布の形状によって、下記3つを取ることが多い。
- 平行平板のとき:面積S、高さhの直方体
- 円筒型のとき:半径r、高さ1の円筒
- 球形のとき:半径rの球
それぞれのパターンに共通することは、どの電気力線もその時に取った閉曲面Sを垂直に貫いていることです。もし、垂直以外の成分を持ちながら斜めに鎖交しているときは、\(cos\theta\)など、垂直成分に分解しなければならず、計算が非常に面倒となります。しかし、このような懸念は上記3パターンの閉曲面の取り方では起こらず、全て綺麗に鎖交します。
平板コンデンサにおけるガウスの法則
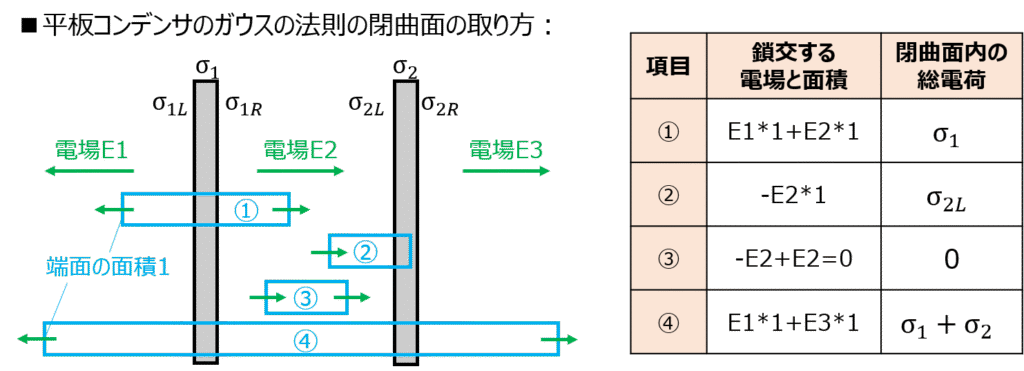
前節にて、“直方体を適用する”と説明しましたが、適用する場所によって結果も変わってきます。
例えば、①平板をまたがるように直方体を置いた場合は、左右の面にて電気力線が垂直に貫きます。だから、\(\int_{S} \boldsymbol{E}・d\boldsymbol{S}=2E・S\)のように、係数に2が付きます。
一方で、②左右片方の面を導体内に取った時は、もう一方の面しか垂直に貫きません。よって、\(\int_{S} \boldsymbol{E}・d\boldsymbol{S}=E・S\)と、係数は1になります。
他にも、③導体をまたがない中空の場所でのみ閉曲面を取った場合は、左でn本貫いたのに、右では-n本貫くことがあります。(向きの都合上)
このような場合は、閉曲面を貫く電気力線の本数はトータルで0本となります。
最後に、④無限の長さの閉曲面を取った時は、中空部分の長さを無視することができ、面密度\(\sigma_{1}+\sigma_{2}\)の1つの導体から左右に電場が発生するとできます。よって、左右の電場は=になります。
以上のように、様々な閉曲面の取り方をし、その時の式を連立して未知数を決定していきます。
解答例
電場分布
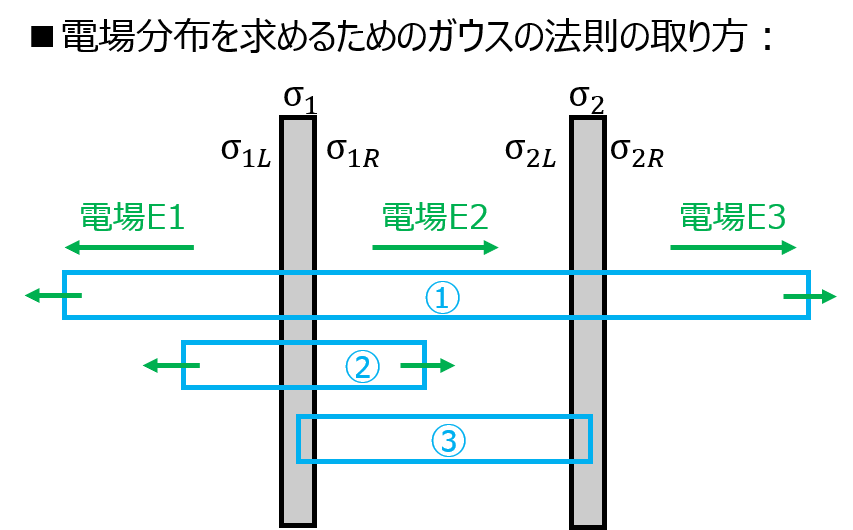
下記の区間の直方体(左右の端面の面積が1)を取り、ガウスの法則を適用する。
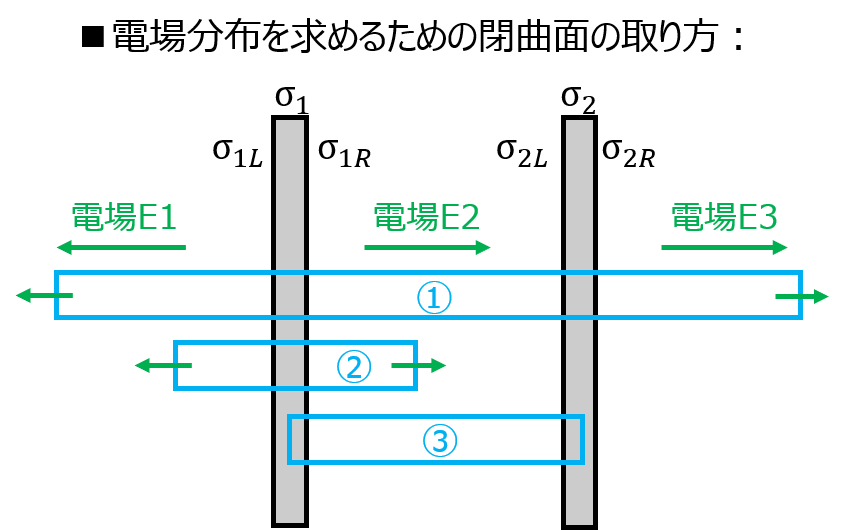
- 左右の距離∞の無限遠に延びる直方体
- 導体1にまたがる直方体
- 直方体の左右の端面がそれぞれ導体1,2内部に存在する直方体
1.について、前節より、左右の無限遠どちらからでも\(\sigma_{1}+\sigma_{2}\)の面電荷が同じ場所に帯電しているとみなせるので、
\begin{aligned}E_{1}=E_{3}=\dfrac{\sigma_{1}+\sigma_{2}}{2\varepsilon_{o}} \end{aligned}
※左右の端面に電場が直交するため、面積1+1=2。だから分母に2が付きます。
2.について、左の端面では電場\(E_{1}\)が面積1の分鎖交し、右の端面では電場\(E_{2}\)が同じく面積1鎖交するため
\begin{aligned}E_{1}+E_{2}=\dfrac{\sigma_{1}}{\varepsilon_{o}}\end{aligned}
これに1.の結果(2)式を代入し
\begin{aligned}E_{2}=\dfrac{\sigma_{1}-\sigma_{2}}{2\varepsilon_{o}}\end{aligned}
以上より、電場\(E_{1},E_{2},E_{3}\)が全て求められた。
電荷分布
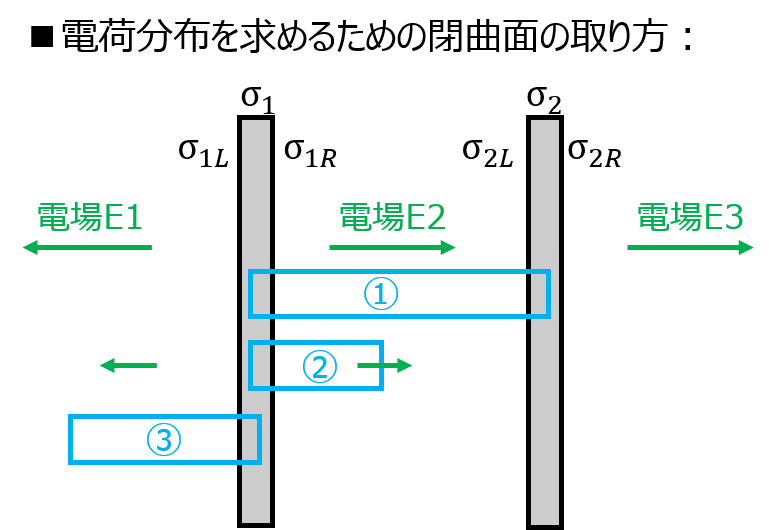
導体ごとの左右に帯電する電荷を区別する特性上、端面の一方(または両方)は導体内で閉曲面を取ることが多いです。
- 左の端面は導体1内部、右の端面は導体2内部を取る直方体
- 左の端面は導体1内部、右の端面は導体1,2の中空を取る直方体
- 左の端面は導体1左の真空、右の端面は導体1の内部を取る直方体
1.について、導体内部に電場は発生しない。ガウスの法則の右辺は0になるので
\begin{aligned}\sigma_{1R}+\sigma_{2L}=0\end{aligned}
2.について、\(\sigma_{1R}\)から発生する電場\(E_{2}\)が直方体の左面を貫くので
\begin{aligned}E_{2}=\dfrac{\sigma_{1R}}{\varepsilon_{o}}=\dfrac{\sigma_{1}-\sigma_{2}}{2\varepsilon_{o}}\end{aligned}
3.について、\(\sigma_{1L}\)から発生する電場\(E_{1}\)が直方体の左面を貫くので
\begin{aligned}E_{1}=\dfrac{\sigma_{1L}}{\varepsilon_{o}}=\dfrac{\sigma_{1}+\sigma_{2}}{2\varepsilon_{o}}\end{aligned}
式(5)~(7)をまとめて
\begin{cases}\sigma_{1L}=\dfrac{\sigma_{1}+\sigma_{2}}{2} \\ \sigma_{1R}=\dfrac{\sigma_{1}-\sigma_{2}}{2} \\ \sigma_{2L}=\dfrac{\sigma_{2}-\sigma_{1}}{2} \\ \sigma_{2R}=\dfrac{\sigma_{1}+\sigma_{2}}{2} \end{cases}
最後に
分かりやすいように閉曲面は直方体で考えましたが、円筒でも構いません。ただ、端面の面積は1で考えた方が後々の計算が楽になります。