コルピッツ発振器とハートレー発振器の発振条件

電子回路

2024.06.182024.06.23

問題

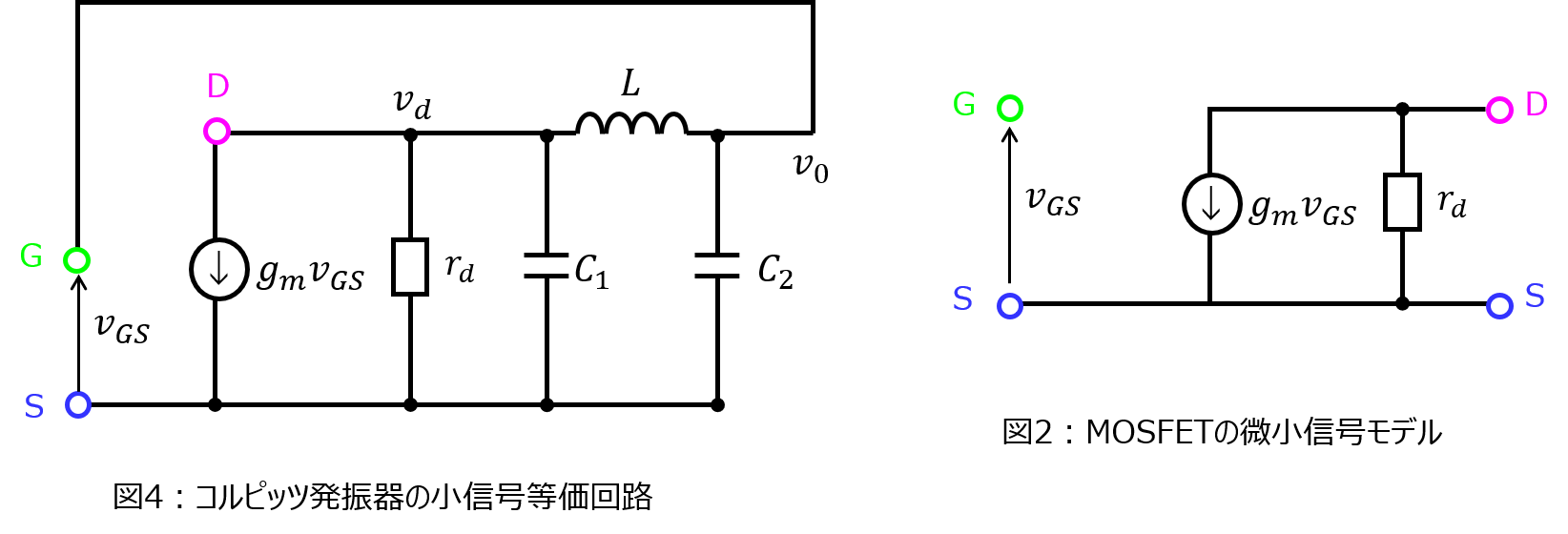
下記にMOSFETを用いたコルピッツ発振器とハートレー発振器を示す。それぞれの発振条件(振幅条件と周波数条件)を算出せよ。

はじめに
解答
最後に

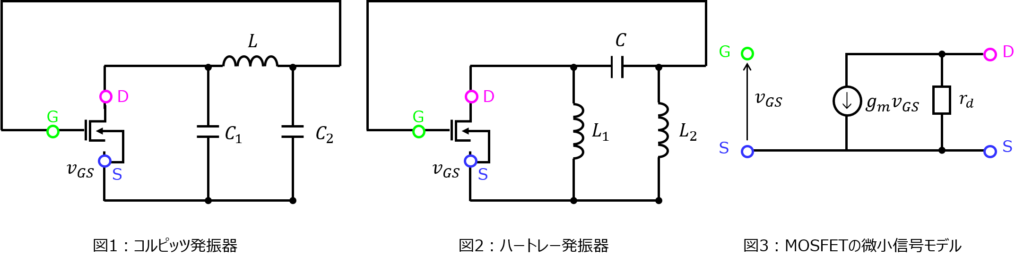
はじめに

発振回路の性質は、前回の記事で説明しました。

本記事では、実際に存在する発振回路の発振条件を問題形式で見ていきます。

ループ利得\(AH\)の実部が1以上、虚部が0である大方針に基づいて解いていきます。

解答

コルピッツ発振器

増幅器(MOSFET)の先にコンデンサが並列に、コイルが間に直列に入っている回路です。

与えられた微小信号モデルにより、下記の等価回路に置き換えることができる。

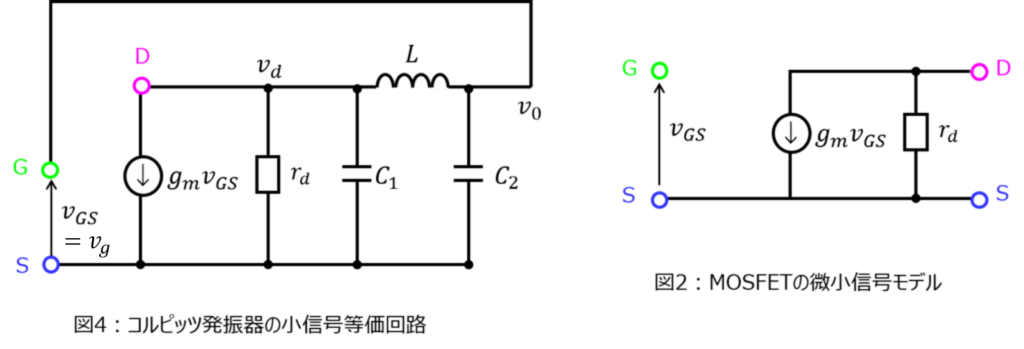
ループ利得\(AH\)は、入力電圧\(v_{g}\)と出力電圧\(v_{o}\)の間に\(v_{d}\)を設定することで、下記で表すことができる。

\begin{aligned}AH=\dfrac{v_{o}}{v_{g}}=\dfrac{v_{d}}{v_{g}}･\dfrac{v_{o}}{v_{d}}\end{aligned}

電流源から右を見たアドミタンスは下記で表すことができる。

\begin{aligned}Y_{d}=\dfrac{1}{r_{d}}+j \omega C_{1}+\dfrac{1}{j \omega L +\frac{1}{j \omega C_{2}}}\end{aligned}

以上より、\(v_{d}\)は

\begin{aligned}v_{d}&=-g_{m}v_{g}Z_{d} \\ &=\dfrac{-g_{m}v_{g}}{\dfrac{1}{r_{d}}+j \omega C_{1}+\dfrac{1}{j \omega L +\frac{1}{j \omega C_{2}}}}\end{aligned}

次に、\(v_{o}\)は、分圧の関係により

\begin{aligned}v_{o}=\dfrac{\frac{1}{j \omega C_{2}}}{j \omega L +\frac{1}{j \omega C_{2}}}v_{d}\end{aligned}

以上より、求めるループ利得は、(3)(4)を(1)に代入して

\begin{aligned}AH=\dfrac{-g_{m}}{\dfrac{1}{r_{d}}+j \omega C_{1}+\dfrac{1}{j \omega L +\frac{1}{j \omega C_{2}}}}\dfrac{\frac{1}{j \omega C_{2}}}{j \omega L +\frac{1}{j \omega C_{2}}}\end{aligned}

これから発振条件を求める。

まず、周波数条件\(Im(AH)=0\)について、上式の分母の虚部に注目し

\begin{aligned}j \omega C_{1}+\dfrac{1}{j \omega L +\frac{1}{j \omega C_{2}}}=0 \\ \omega =\sqrt{\dfrac{C_{1}+C_{2}}{LC_{1}C_{2}}}\end{aligned}

まず、振幅条件について、\(Re(AH)≧1\)だから

\begin{aligned}\dfrac{1}{\frac{1}{r_{d}}} \dfrac{\frac{1}{\omega C_{2}}}{\omega L – \frac{1}{\omega C_{2}}}≧1 \\ g_{m}r_{d}\dfrac{1}{\omega^{2}LC_{2}-1}≧1\end{aligned}

(6)を代入することで

\begin{aligned}g_{m}r_{d}\dfrac{C_{1}}{C_{2}}≧1\end{aligned}

を得る。(振幅条件)

ハートレー発振器

コルピッツ発振器からコイルとコンデンサを逆にした回路です。

小信号等価回路は

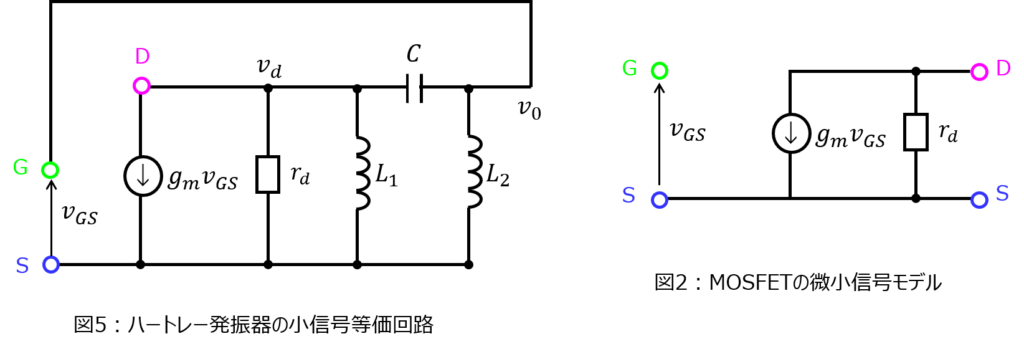
電流源から右を見たアドミタンスは

\begin{aligned}Y_{d}=\dfrac{1}{r_{d}}+\dfrac{1}{j \omega L_{1}}+\dfrac{1}{j \omega L_{2} +\frac{1}{j \omega C_{2}}}\end{aligned}

これより、\(v_{d},v_{o}\)は

\begin{cases}v_{d}&=-g_{m}v_{g}Z_{d} \\ &=\dfrac{-g_{m}v_{g}}{\dfrac{1}{r_{d}}+\frac{1}{j \omega L_{1}}+\dfrac{1}{j \omega L_{2} +\frac{1}{j \omega C}}} \\ v_{o}&=\dfrac{j \omega L_{2}}{j \omega L_{2} +\frac{1}{j \omega C}}v_{d} \end{cases}

以上より、ループ利得は

\begin{aligned}AH=\dfrac{-g_{m}}{\dfrac{1}{r_{d}}+\frac{1}{j \omega L_{1}}+\dfrac{1}{j \omega L_{2} +\frac{1}{j \omega C_{2}}}}\dfrac{j \omega L_{2}}{j \omega L_{2} +\frac{1}{j \omega C}}\end{aligned}

周波数条件は、\(Im(AH)=0\)より

\begin{aligned}\dfrac{1}{j \omega L_{1}}+\dfrac{1}{j \omega L_{2}+\frac{1}{j \omega C}}=0 \\ j \omega L_{1}+j \omega L_{2}+\dfrac{1}{j \omega C}=0 \\ \omega^{2}C(L_{1}+L_{2})=1 \\ \omega = \dfrac{1}{\sqrt{C(L_{1}+L_{2})}} \end{aligned}

次に、振幅条件は、\(Re(AH)≧1\)より

\begin{aligned}g_{m}r_{d}\dfrac{\omega^{2} L_{2}C}{1- \omega^{2} L_{2}C}≧1\end{aligned}

\(\omega^{2} L_{2}C=\dfrac{L_{2}}{L_{1}+L_{2}}, 1-\omega^{2} L_{2}C=\dfrac{L_{1}}{L_{1}+L_{2}}\)なので、(13)式より

\begin{aligned}g_{m}r_{d}\dfrac{L_{2}}{L_{1}}≧1\end{aligned}