トランジスタ回路について下記の問に答えよ。
(1)エミッタ電流を\(I_{E}\)、コレクタ電流を\(I_{C}\)、ベース電流を\(I_{B}\)としたとき、トランジスタの入出力電流の関係式を示せ。また、その理由を述べよ。
(2)ベース接地電流増幅率\(\alpha\)を求めよ。また、\(\alpha\)を用いてエミッタ接地電流増幅率\(\beta\)、コレクタ接地電流増幅率\(\gamma\)を示せ。
(3)\(\alpha,\beta\)の周波数特性を説明せよ
トランジスタとは
以前の記事で詳しく説明しています。
ベースに電流をかけることにより、コレクタからエミッタへ電流が流れます。出力したエミッタ電流は増幅しているため、電流増幅素子と呼ばれます。増幅の程度は、接地方式により異なります。
そこで、本記事では問題を解くことで増幅の程度を定量的に判断しようと思います。
また、周波数領域によっても増幅の強弱も変わりますので、こちらについても説明しています。
解答例
(1)電流の関係式
エミッタ電流は、ベース電流とコレクタ電流の和に等しいことから、下記で表されます。
\begin{aligned}I_{E}=I_{B}+I_{C}\end{aligned}
物理的に説明しようとすると、下記になります。
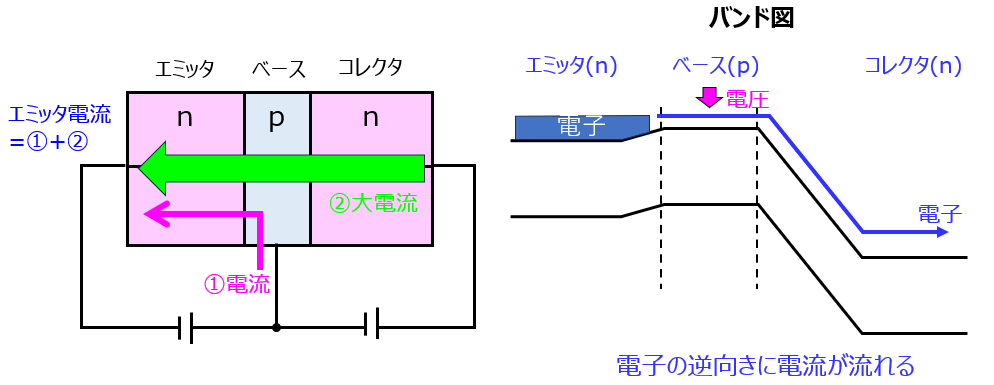
- ベース-エミッタ間に電圧をかけて、ベースからエミッタへベース電流が流れる。
- ベースの準位が下がったため、コレクタからエミッタへ電流が流れる。
- エミッタにて、ベース電流とコレクタ電流が合流する。
この現象を表したものが、式(1)です。電気回路的に入出力の関係だけ考えれば自然と出てくる式ですが、トランジスタ内部では上記の物理現象が発生していることを忘れないでおきましょう。
(厳密には、コレクタからエミッタ流れる電流の一部はベースで再結合しますが、今回は無視しています。)
(2)各接地方式での電流増幅率
過去の記事では、様々な増幅回路での“電圧”増幅率(利得)を説明してきました。
一方で、今回は電流増幅率を説明します。同じ部分もあれば、異なる部分もあります。
試験の際は、電流、電圧のどちらの増幅率を問われているのか、注意深く問題を読みましょう。
ベース接地の電流増幅率
コレクタ電流に対するエミッタ電流の比
\begin{aligned}\alpha=\dfrac{I_{C}}{I_{E}}\end{aligned}
を言います。これは定義なので覚えましょう。
エミッタ接地の電流増幅率
コレクタ電流に対するベース電流の比に対し、(1)式を使用します。
\begin{aligned}\beta=\dfrac{I_{C}}{I_{B}}=\dfrac{I_{C}}{I_{E}-I_{C}}=\dfrac{\alpha}{1-\alpha}\end{aligned}
コレクタ接地の電流増幅率
これはあまり問われないですが、一応説明します。
ベース電流に対するエミッタ電流の比であるため
\begin{aligned}\gamma=\dfrac{I_{E}}{I_{E}-I_{C}}=\dfrac{1}{1-\alpha}\end{aligned}
(3)エミッタ接地電流増幅率の周波数特性
電圧増幅率と同じく、電流増幅率も高周波になると低下します。下記に理由を示していきます。
まず、ベース幅を\(W_{B}\)のトランジスタモデルを考えます。
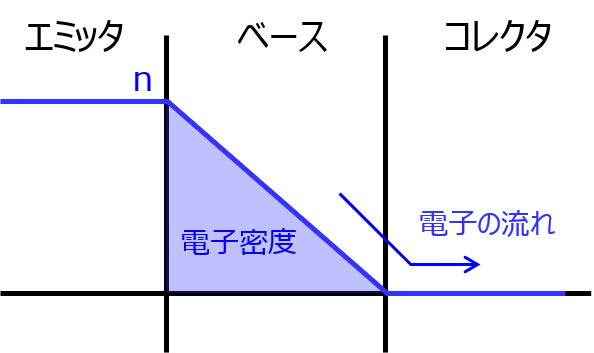
ベース中央の電子速度を\(v\)とすると、電子がベースを通過する時間は下記になります。
\begin{aligned}\tau=\dfrac{W_{B}}{v}\end{aligned}
この式より、入力電圧が切り替わったとして、電子が応答できるには\(\tau\)かかることが分かります。
周波数が\(\frac{1}{\tau}\)より大きい信号に対しては応答できなくなる=増幅できないことが分かります。
高周波の信号に対しては特性が落ちるため、交流電源の位相jを踏まえ、\(\alpha\)は下記のようになります。
\begin{aligned}\alpha=\dfrac{\alpha_{o}}{1+\frac{\omega}{\omega_{a}}}\end{aligned}
(3)式に(6)式を代入し
\begin{aligned}\beta=\dfrac{\frac{\alpha_{o}}{1-\alpha_{o}}}{1+j\frac{\omega}{(1-\alpha_{o})\omega_{a}}}\end{aligned}
と表すことができます。ともに、高周波になると特性が低下することが分かりました。
安定指数
エミッタ接地回路は増幅に優れていますが、それ故に外乱によって出力電流、電圧が変動します。
変動度合いは、安定指数によって評価します。
例として、下記の増幅回路を考えます。
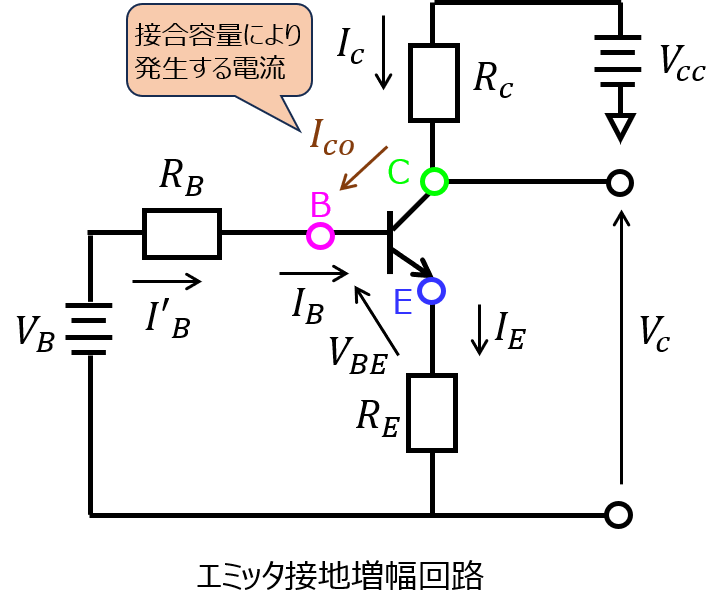
前章までの説明より、エミッタ電流は増幅率\(\beta\)を用いて
\begin{aligned}I_{E}=(1+\beta)I_{B}\end{aligned}
になります。コレクタ-ベース間の電流を\(I_{co}\)とすると
\begin{aligned}I’_{B}=I_{B}-I_{co}=\dfrac{I_{E}}{1+\beta}-I_{co}\end{aligned}
\begin{aligned}I_{c}=\beta I_{B}+I_{co}\end{aligned}
ベース電圧\(V_{B}\)は、下記で表されます。
\begin{aligned}V_{B}=R_{B}I’_{B}+V_{BE}+R_{E}(1+\beta)I_{B}\end{aligned}
これを変形し、ベース電流\(I_{B}\)を表すと
\begin{aligned}I_{B}=\dfrac{V_{B}-V_{BE}+R_{B}I_{co}}{R_{B}+(1+\beta)R_{E}}\end{aligned}
(10)式に結果を代入すると、コレクタ電流は
\begin{aligned}I_{c}=\dfrac{\frac{\beta(V_{B}-V_{BE})}{1+\beta}+(R_{E}+R_{B})I_{co}}{R_{E}+\frac{R_{B}}{1+\beta}}\end{aligned}
これを用いて、出力電圧\(V_{c}=V_{cc}-R_{c}I_{c}\)は
\begin{aligned}V_{c}=V_{cc}-R_{c}\dfrac{\frac{\beta(V_{B}-V_{BE})}{1+\beta}+(R_{E}+R_{B})I_{co}}{R_{E}+\frac{R_{B}}{1+\beta}}\end{aligned}
トランジスタ素子にかかる\(V_{BE},I_{co}\)が\(V_{c}\)の変動に影響を及ぼすので、その分の項を抜き出すと
\begin{cases}S_{v}=R_{c}・\dfrac{\frac{\beta}{1+\beta}}{R_{E}+\frac{R_{B}}{1+\beta}} \\ S_{i}=\dfrac{R_{E}+R_{B}}{R_{E}+\frac{R_{B}}{1+\beta}}\end{cases}
となります。それぞれ、電圧安定指数、電流安定指数となっています。
安定指数は、小さいほど出力電圧の変動が小さく、良いと解釈します。

