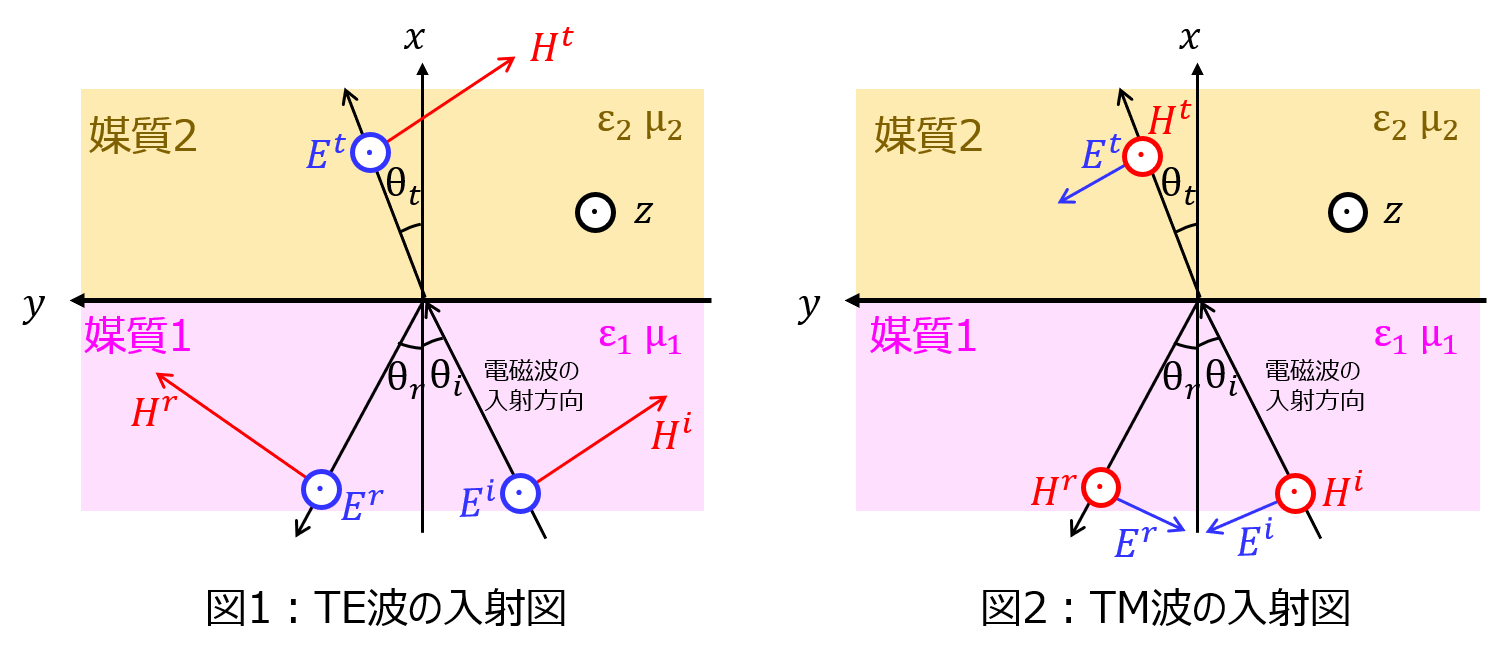
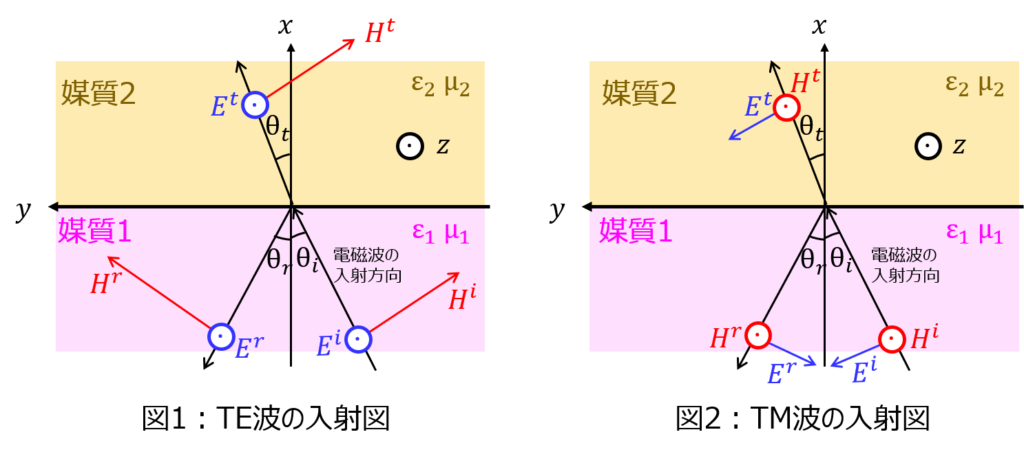
媒質1から媒質2へ電磁波が斜めに入射する。
(1)電場\(\boldsymbol{E}\)が境界面に対して平行であるTE波
(2)磁場\(\boldsymbol{H}\)が境界面に対して平行であるTM波
上記2通りについて、境界条件が成立するときの\(\theta_{i},\theta{r}\)の関係。反射係数、透過係数をそれぞれ求めよ。
また、(2)TM波について、\(\mu_{1}=\mu_{2}\)で反射係数が0になるときの\(\theta_{i}\)を求めよ。
はじめに
本問は、計算がしんどいです。電磁波の入射方向、電場の向き、磁場の向きにそれぞれ気を付けて立式していかないと、たちまち計算ミスします。
電磁波の式の見方については、過去の記事で紹介しました。本問では、これを参考にしながら解いていきます。
どちらかと言うと、理学部の院試に出てきやすい問題です。関係者は、本問が参考になると幸いです。
他サイトでは、途中の計算過程を端折りがちですが、本記事では省略することなく記載していきます。
だいぶ長文になりましたので、必要な部分だけ確認することをオススメします。
本記事で覚えたいこと
- 入射波、反射波、透過波それぞれの式を電場、磁場に対して記載する
- 境界条件により、yz平面に平行な成分の(入射波+反射波)=透過波の関係を電場、磁場に対して適用する。
- 反射係数\(R=\dfrac{E_{r}}{E_{i}}\)、透過係数\(T=\dfrac{E_{t}}{E_{i}}\)と、入射波に対する比を取り、各係数を求める。
例えばですが、TE波の入射波の電場成分は、図1よりz成分しかないです。このため、下記の式で表すことができます。
\begin{eqnarray}E_{z}^{i}=E_{i}\exp \left( -jk_{1}\left( y\sin \theta _{i}+x\cos \theta _{i}\right) \right)\end{eqnarray}
\(\exp\)項以前は、電場の成分で符号を合わせます。図1より電場は+z方向を向いているので負は付きません。
\(\exp\)項内部は、電磁波の進行方向を示します。xy平面上で斜め入射しているため、成分分解して+y方向は\(y \sin\theta\)、+x方向は\(x \cos\theta\)で表すことができます。
仮に反射波だったとすると、図1より、電磁波の進行方向(x成分)は負を向いています。よって、\(\exp\)項内部は、\(\left (y\sin \theta _{i}-x\cos \theta _{i}\right) \)と、x成分は負になります。
入射波だけでなく反射波、透過波についても同様に立式します。その後、境界条件を取れば透過係数、反射係数を求めることができます。
解答例
(1)前半 TE波の性質 (スネルの法則)
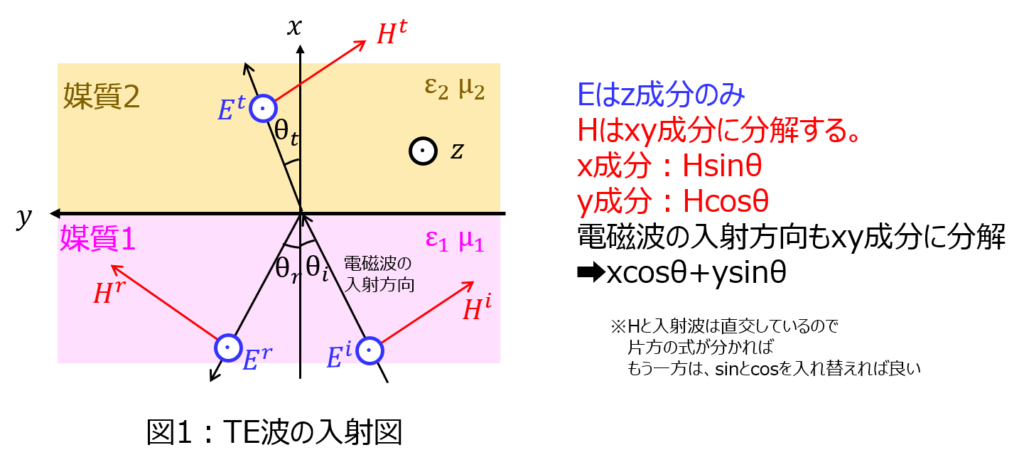
与えられた図から、入射波は以下の式で表すことができる。
\begin{cases}E_{z}^{i}=E_{i}\exp \left( -jk_{1}\left( y\sin \theta _{i}+x\cos \theta _{i}\right) \right) \\ H_{x}^{i}=H_{i}\sin\theta_{i} \exp \left( -jk_{1}\left( y\sin \theta _{i}+x\cos \theta _{2}\right) \right) \\ H_{y}^{i}=-H_{i}\cos\theta_{i} \exp \left( -jk_{1}\left( y\sin \theta _{i}+x\cos \theta _{2}\right) \right) \end{cases}
反射波についても、下記の式で表すことができる。
\begin{cases}E_{z}^{r}=E_{r}\exp \left( -jk_{1}\left( y\sin \theta _{r}+x\cos \theta _{r}\right) \right) \\ H_{x}^{i}=H_{i}\sin\theta_{i} \exp \left( -jk_{1}\left( y\sin \theta _{i}+x\cos \theta _{2}\right) \right) \\ H_{y}^{i}=-H_{i}\cos\theta_{i} \exp \left( -jk_{1}\left( y\sin \theta _{i}+x\cos \theta _{2}\right) \right) \end{cases}
透過波についても、下記の式で表すことができる。
\begin{cases}E_{z}^{t}=E_{t}\exp \left( -jk_{2}\left( y\sin \theta _{t}+x\cos \theta _{t}\right) \right) \\ H_{x}^{t}=H_{t}\sin\theta_{t} \exp \left( -jk_{2}\left( y\sin \theta _{t}+x\cos \theta _{2}\right) \right) \\ H_{y}^{t}=-H_{t}\cos\theta_{t} \exp \left( -jk_{2}\left( y\sin \theta _{t}+x\cos \theta _{t}\right) \right) \end{cases}
境界条件により、\(x=0\)で電場\(E\)と磁場\(H\)の接線成分は連続。
\begin{cases}E_{y}^{i}+E_{y}^{r}=E_{y}^{t} \\ H_{z}^{i}+H_{z}^{r}=H_{z}^{t} \end{cases}だから、()~()にx=0を代入して
\begin{cases}E_{i}\exp(-jk_{1}y\sin\theta_{i})+E_{r}\exp(-jk_{1}y\sin\theta_{r})=E_{t}\exp(-jk_{2}y\sin\theta_{t}) \\ -H_{i}\cos\theta_{i}\exp(-jk_{1}y\sin\theta_{i})+H_{r}\cos\theta_{r}\exp(-jk_{1}y\sin\theta_{r})=-H_{t}\cos\theta_{t}\exp(-jk_{2}y\sin\theta_{t}) \end{cases}
任意のyに対し上記の式が成立するためには、\(E\)、\(H\)ともに\(\exp\)項の内部に注目し
\begin{aligned}k_{1}y\sin \theta_{i}=k_{1}y\sin \theta_{r}=k_{2}y\sin \theta _{t} \\ \end{aligned}
\begin{cases}\theta_{i}=\theta_{ r} \\ k_{1}\sin \theta_{i}=k_{2}\sin \theta _{t}\end{cases}
の条件が成立する必要がある。(スネルの法則)
(1)後半 TE波の反射係数、透過係数
任意の\(H\)に対し、
\begin{eqnarray}E=\dfrac{H}{Z}\end{eqnarray}の条件を適用する。(Zは媒質中の固有インピーダンス。
\begin{cases}E_{y}^{i}+E_{y}^{r}=E_{y}^{t} \\ \dfrac{E_{i}-E_{r}}{Z_{1}}\cos\theta_{i}=\dfrac{E_{t}}{Z_{2}}\cos \theta_{t} \end{cases}
\begin{eqnarray}\dfrac{E_{i}-E_{r}}{Z_{1}}\cos \theta_{i}=\dfrac{E_{i}+E_{r}}{Z_{2}}\cos \theta_{t} \\ \left( \dfrac{\cos \theta _{i}}{Z_{1}}-\dfrac{\cos \theta _{t}}{Z_{2}}\right) E_{i} =\left( \dfrac{\cos \theta _{i}}{Z_{1}}+\dfrac{\cos \theta _{t}}{Z_{2}}\right) E_{r} \\ R_{TE}=\dfrac{E_{r}}{E_{i}}=\dfrac{\left( \dfrac{\cos \theta _{i}}{Z_{1}}-\dfrac{\cos \theta _{t}}{Z_{2}}\right)}{\left( \dfrac{\cos \theta _{i}}{Z_{1}}+\dfrac{\cos \theta _{t}}{Z_{2}}\right)} \\ = \dfrac{Z_{2}\cos \theta {i}-Z{1}\cos \theta {t}}{Z{2}\cos \theta {i}+Z{1}\cos \theta_{t}} \end{eqnarray}
透過係数についても、同様にして
\begin{eqnarray}\dfrac{E_{i}-\left( E_{i}+E_{t}\right) }{Z_{1}}\cos \theta {i}=\dfrac{E{t}}{Z_{2}}\cos \theta _{t} \\ 2Z_{2}E_{i}\cos \theta_{i}=Z{1}E_{t}\cos \theta_{i}+Z_{2}E_{t}\cos \theta_{t} \\ T_{TE}=\dfrac{E_{t}}{E_{i}}=\dfrac{2Z_{2}\cos \theta _{i}}{Z{2}\cos \theta_{i}+Z{1}\cos \theta _{t}}\end{eqnarray}
※反射”係数” と 透過”係数”の合計値は1になりません。だから、\(T_{TE}=1-R_{TE}\)と計算することなく、それぞれ定義に基づいて解答しています。(間違いやすい)
(2)前半 TM波の性質(スネルの法則)
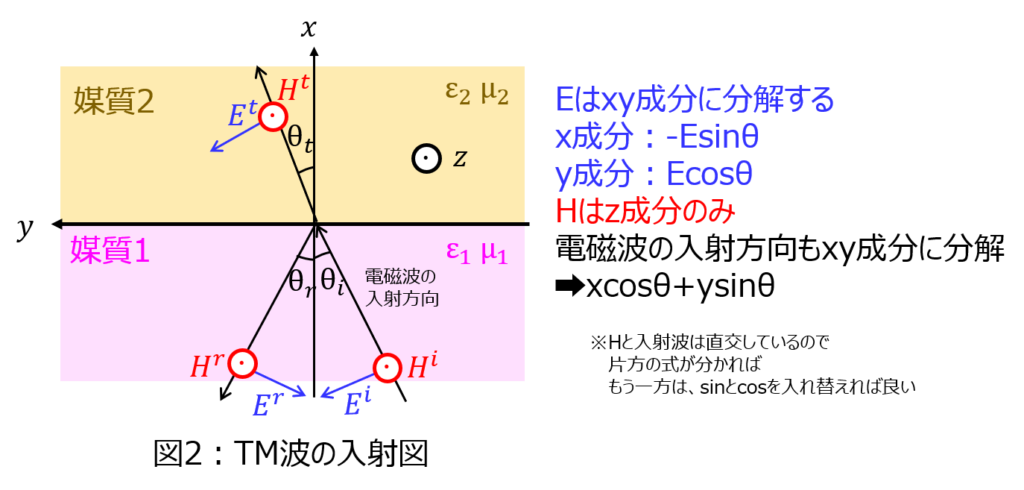
基本的にTE波と同様にして、解くことができます。
ですので、前半は見る必要が無いかもしれません。
ただし、\(\mu_{1}=\mu_{2}\)のとき、TM波特有の現象を導くことができます。(ブリュースター角)
ページ下部にありますので、そこだけでもご覧ください。
<入射波>
\begin{cases}E_{x}^{i}=-E_{i}\sin \theta_{i} \exp \left( -jk_{1}\left( y\sin \theta _{i}+x\cos \theta _{i}\right) \right) \\ E_{y}^{i}=E_{i}\cos \theta_{i} \exp \left( -jk_{1}\left( y\sin \theta _{i}+x\cos \theta _{i}\right) \right) \\ H_{z}^{i}=H_{i} \exp \left( -jk_{1}\left( y\sin \theta _{i}+x\cos \theta _{i}\right) \right) \end{cases}
<反射波>
\begin{cases}E_{x}^{r}=-E_{r}\sin \theta_{r} \exp \left( -jk_{1}\left( y\sin \theta _{r}+x\cos \theta _{r}\right) \right) \\ E_{y}^{r}=-E_{r}\cos \theta_{r} \exp \left( -jk_{1}\left( y\sin \theta _{r}-x\cos \theta _{r}\right) \right) \\ H_{z}^{r}=H_{r} \exp \left( -jk_{1}\left( y\sin \theta _{r}-x\cos \theta _{r}\right) \right) \end{cases}
<透過波>
\begin{cases}E_{x}^{t}=-E_{t}\sin \theta_{t} \exp \left( -jk_{2}\left( y\sin \theta _{t}+x\cos \theta _{t}\right) \right) \\ E_{y}^{t}=E_{t}\cos \theta_{t} \exp \left( -jk_{2}\left( y\sin \theta _{t}+x\cos \theta _{t}\right) \right) \\ H_{z}^{t}=H_{t} \exp \left( -jk_{2}\left( y\sin \theta _{t}+x\cos \theta _{t}\right) \right) \end{cases}
境界条件により、\(x=0\)で電場\(E\)と磁場\(H\)の接線成分は連続。
\begin{cases}E_{i}\cos \theta_{i}\exp \left( -jk_{1}y\sin \theta _{i}\right) -E_{r}\cos \theta_{r}\exp \left( -jk_{1}y\sin \theta _{r}\right)=E_{t}\cos \theta {i}\exp \left( -jk_{2}y\sin \theta _{t}\right) \\ H_{i}\exp \left( -jk_{1}y\sin \theta _{i}\right) + H_{r}\exp \left( -jk_{1}y\sin \theta _{r}\right)=H_{t}\exp \left( -jk_{1}y\sin \theta _{t}\right)\end{cases}
任意のyに対し上記の式が成立するためには、\(E\)、\(H\)ともに\(\exp\)項の内部に注目し
\begin{aligned}k_{1}y\sin \theta_{i}=k_{1}y\sin \theta_{r}=k_{2}y\sin \theta _{t} \\ \end{aligned}
\begin{cases}\theta_{i}=\theta_{r} \\ k_{1}\sin \theta _{i}=k_{2}\sin \theta _{t}\end{cases}
の条件が成立する必要がある。(スネルの法則)
TM波についても同じく証明することができました。
(2)後半 TM波の反射係数、透過係数 (ブリュースター角)
TE波と同様にして、境界条件は
\begin{cases}\left( E_{i}-E_{r}\right) \cos \theta_{i}=E{t}\cos \theta {i} \\ \dfrac{E_{i}+E_{r}}{Z_{1}}=\dfrac{E_{t}}{Z_{2}}\end{cases}
第2式より、
\begin{eqnarray}E_{t}=\dfrac{Z_{2}}{Z_{1}}(E_{i}+E_{r})\end{eqnarray}
これを第1式に代入して
\begin{eqnarray}(E_{i}-E_{r})\cos \theta_{i}=\dfrac{Z_{2}}{Z_{1}}(E_{i}+E_{r}) \\ \left( \cos \theta_{i} -\dfrac{Z_{2}}{Z_{1}}\cos \theta_{t} \right) E_{i}=\left( \cos \theta_{i} +\dfrac{Z_{2}}{Z_{1}}\cos \theta_{t} \right) E_{r} \\ R_{TM}=\dfrac{E_{r}}{E_{i}}= \dfrac{Z_{1}\cos \theta_{i} -Z_{2}\cos \theta_{t}}{Z_{1}\cos \theta +Z_{2}\cos \theta_{t}}\end{eqnarray}
透過波についても同様にして、第2式から
\begin{eqnarray}E_{r}=-E_{i}+\dfrac{Z_{1}}{Z_{2}}E_{t}\end{eqnarray}
これを第1式に代入し
\begin{eqnarray}\left( E_{i}+E_{i}-\dfrac{Z_{1}}{Z_{2}}E_{t}\right) \cos \theta_{i} =E_{t}\cos \theta_{t} \\ T_{TM}=\dfrac{E_{t}}{E_{i}}= \dfrac{2Z_{2}\cos \theta_{i}}{Z_{1}\cos \theta_{i}+Z_{2}\cos \theta_{t}}\end{eqnarray}
(2)最後 ブリュースター角
スネルの法則より、
\begin{eqnarray}\sin \theta_{t}=\dfrac{k_{1}}{k_{2}}\sin \theta_{i}\end{eqnarray}
波数\(k\)は下記のように表すことができる。
\begin{eqnarray}k_{1}=\omega \sqrt{\varepsilon_{1} \mu_{1}} \\ k_{2}=\omega \sqrt{\varepsilon_{2} \mu_{2}}\end{eqnarray}
\(\mu_{1}=\mu_{2}\)より、
\begin{eqnarray}\dfrac{k_{1}}{k_{2}}=\sqrt{\dfrac{\varepsilon_{1}}{\varepsilon_{2}}}\sin \theta_{i}\end{eqnarray}
三角関数の定義により
\begin{eqnarray}\cos\theta_{t}=\sqrt{1-\sin^{2}\theta_{t}}=\sqrt{1-\dfrac{\varepsilon_{1}}{\varepsilon_{2}}\sin^{2}\theta_{i}}\end{eqnarray}
これを反射係数の式に代入し
\begin{eqnarray}R_{TM}=\dfrac{Z_{1}\cos \theta_{i} -Z_{2}\sqrt{1-\dfrac{\varepsilon }{\varepsilon {2}}\sin \theta_{i} }}{Z{1}\cos \theta_{i} +Z_{2}\sqrt{1-\dfrac{\varepsilon_{1}}{\varepsilon {2}}\sin \theta_{i} }}\end{eqnarray}
これが0になれば良いので、分子に注目し
\begin{eqnarray}Z_{1}^{2}\cos ^{2}\theta_{i} =Z_{2}^{2}\left( 1-\dfrac{\varepsilon_{1}}{\varepsilon_{2}}\sin ^{2}\theta_{i} \right)\end{eqnarray}
\(Z_{1}=\sqrt{\mu_{1}}{\varepsilon_{1}},Z_{2}=\sqrt{\mu_{2}}{\varepsilon_{2}}\)で、\(\mu_{1}=\mu_{2}\)
\begin{eqnarray}1+\tan^{2} \theta=\dfrac{1}{\cos^{2} \theta}\end{eqnarray}
なので
\begin{eqnarray}\dfrac{1}{\varepsilon {1}}=\dfrac{1}{\varepsilon {2}}\left( 1+\tan ^{2}\theta -\dfrac{\varepsilon _{1}}{\varepsilon {2}}\tan ^{2} \theta _{1}\right) \\ \dfrac{\varepsilon _{2}-\varepsilon _{1}}{\varepsilon _{2}}\tan ^{2}\theta =\dfrac{\varepsilon _{2}-\varepsilon _{1}}{\varepsilon _{1}} \\ \tan^{2} \theta_{i}=\dfrac{\varepsilon_{2}}{\varepsilon _{1}}\end{eqnarray}
のとき、反射係数が0になることが分かった。これをブリュースター角と言う。
最後に
計算量が非常に多いですが、やることとしてはワンパターンです。是非何度も練習して自分のものにしてください。