フェーザ表示とは？基準電圧の説明と変換方法の例題を紹介

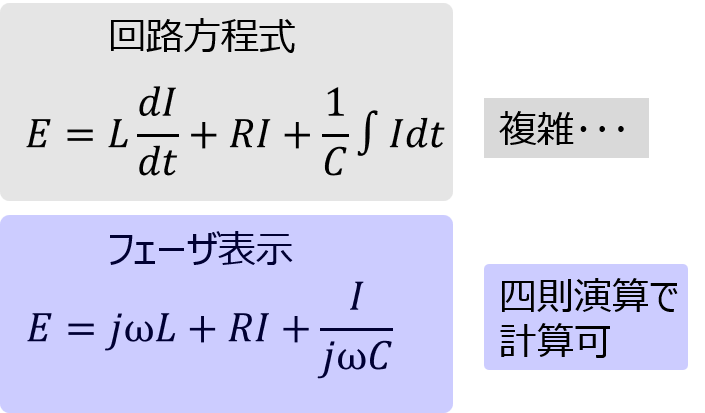
フェーザ表示とは

計算式に存在する三角関数から時間の概念を省略し、実効値(複素数表示)で表記する形式です。

交流信号は周期的に変化するため、ある時間で計測した電流、電圧値は別の時間でも同じ値を取ることが予想できます。

このことから、0から∞までの時間において各値を逐次求める必要は無いです。同一周期の中で電流、電圧値、インピーダンスが基準位相に対してどれくらい離れているのかさえ分かれば、後はそれが繰り返しであると考えれば良いです。

フェーザ表示は、上記の考えを達成するための手段です。

院試の電気回路でも、フェーザ表示を用いて解く問題がかなりの割合を占めており、頻出分野になっています。

フェーザ表示の例と利点

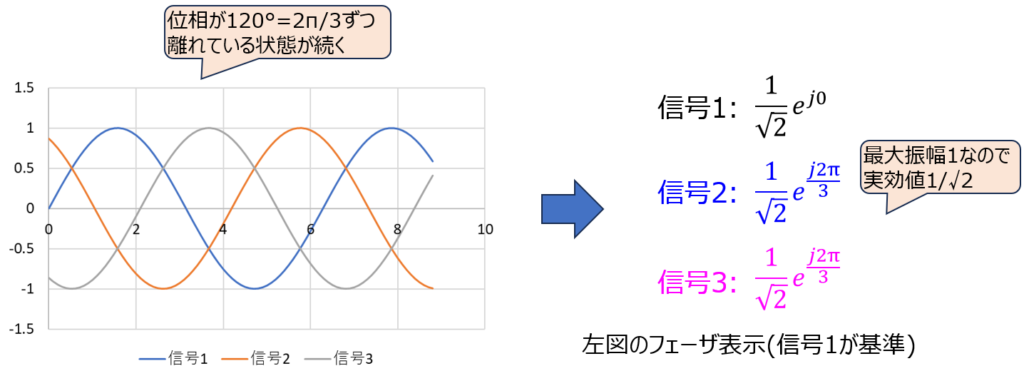
2√2sinωtの正弦波のフェーザ表示を考えます。sinωtを基準の位相とし、実効値1/√2を乗算すると、フェーザ表示は“2exp(j0)”になります。大変簡略化できました。

他、2√2sinωtの時間微分を考えたとき、2√2ωcosωtになります。sin(ωt+π/2)=cosωtにより、基準位相に対し+π/2進んでいることが分かります。

e^{j π/2}=+jから、微分項は+jωで表すことができると分かります。

積分項の場合は、微分と逆のことをするため、1/jωになります。

このため、下記の利点があります。

当然に見えて凄い効果です。微分項、積分項が含まれていると、微分方程式を解く問題と化してしまい、人間の手で解ける場面は限られてきます。一方で、フェーザ表示ならば高校数学の複素数の知識で回路パラメータを求められます。

このように、回路方程式を解くために必要な計算量を大幅に低減できます。

フェーザ表示から時間項に戻す際は、基準位相に注意して振幅を√2倍すれば良いです。一度フェーザ表示にすると時間表示に戻せないことは無いので、この計算を行ってもデメリットがありません。

フェーザ表示の注意点

基本的にメリットばかり目立ちますが、使用に際しては注意すべき点もあります。

1.について、フェーザ表示は過渡解析を行うときには使用できません。なぜならば、回路を動作させていない状態で電流を流すと、最初はコイルの誘導起電力の成分が強くなります。また、コンデンサに電圧がかかっていません。

この影響をフェーザ表示では表現できないです。よって、十分時間が経ち、コイル、コンデンサの動作が定常状態に落ち着いた時、どのような位相差、振幅になっているのか。を確認する観点で使用します。

2.について、前節に正弦波が出て来たことから自明かもしれませんが、直流の場合は使用しません。この場合、定常状態ではコイルに電圧は立たず、コンデンサには電圧が立っているつもりで回路を近似して電流特性を求めます。

3.について、基準となる位相は問題によって変わります。本記事ではsinωtを基準としましたが、cosωtを基準とする場合もあります。この場合は、sinはcosに対しπ/2位相が遅れることから、-jで表記する必要があります。是非、基準の位相をチェックしてから解きましょう。

現場の電気用品の表記方法について

電力系統を見ると分かるように、昨今の電気機器は交流で動くものが圧倒的に多いです。そのため、定格電圧、出力などは”実効値”で表記されています。

同じく、電流を計測するテスターも実効値で表示しています。瞬時値(振幅)で表現しているわけでは無いです。将来、電気工作をする際には、この表記を念頭に置いて進めていきましょう。

解答例

時間関数⇒フェーザ表示の変換

(1)$v(t)=10\sin (\omega t+{\displaystyle \frac{\pi }{4}})$

基準位相はsinなので、与えられた信号は+π/4進み。フェーザ表示の場合は、信号の振幅を1/√2倍する。このため、フェーザ表示での振幅は5√2になる。

このことから、下記のようにフェーザ表示できる。

$$\begin{array}{}\text{(1)}& \begin{array}{r}V=5\sqrt{2}{e}^{j\frac{\pi }{4}}\end{array}\end{array}$$

(2)$v(t)=2\sqrt{2}\sin (\omega t+{\displaystyle \frac{\pi }{3}})$

基準位相に対し、π/3進みで、振幅は2√2 / √2 =2。

求めるフェーザ表示は

$$\begin{array}{}\text{(2)}& \begin{array}{r}V=2e^{\frac{\pi }{3}}\end{array}\end{array}$$

フェーザ表示⇒時間関数の変換

逆の場合もやってみましょう。とはいえ、振幅を√2倍し、位相差分を三角関数(sin)で表現することに注意すれば良いです。

(3)$I=-2-j2$

フェーザ表示上の振幅は、$\sqrt{2^2+2^2}=2\sqrt{2}$

偏角は-3π/4なので

$$\begin{array}{}\text{(3)}& \begin{array}{r}i(t)=4\sin (\omega t-{\displaystyle \frac{3\pi }{4}})\end{array}\end{array}$$

(4)$V=1$

複素数jを持たないことから、基準位相sinωtと同じ位相。

振幅だけ√2倍すれば良いので

$$\begin{array}{}\text{(4)}& \begin{array}{r}v(t)=\sqrt{2}\sin (\omega t)\end{array}\end{array}$$

(5)$V=j3$

複素数+jが含まれていることから、基準位相sinωtに対しπ/2進んでいます。よって、cos波になります。

振幅は、(4)と同じく√2倍すれば良いので

$$\begin{array}{}\text{(5)}& \begin{array}{r}v(t)=3\sqrt{2}\cos (\omega t)\end{array}\end{array}$$

フェーザ表示を用いた計算

院試ではあまり出てきませんが、フェーザ表示の概念を用いると楽に計算できる場合があります。

電気回路だけでなく数学を勉強することも多いと思います。予備知識に持っておくと良いです。

(6)$I=2\sqrt{2}\sin (t-{\displaystyle \frac{\pi }{3}})+{\displaystyle \frac{d}{dt}}\sqrt{2}\sin (t-{\displaystyle \frac{\pi }{6}})$

与えられた式をフェーザ表示する。微分項は+j⇒exp(π/2)であることに注意すると

$$\begin{array}{}\text{(6)}& \begin{array}{rl}i(t)& =2e^{-j\frac{\pi }{3}}+e^{j\frac{\pi }{2}-j\frac{\pi }{6}}\\ & =2e^{-j\frac{\pi }{3}}+e^{j\frac{\pi }{3}}\\ & =2({\displaystyle \frac{1}{2}}-{\displaystyle \frac{j\sqrt{3}}{2}})+({\displaystyle \frac{1}{2}}+{\displaystyle \frac{j\sqrt{3}}{2}})\\ & ={\displaystyle \frac{3}{2}}-{\displaystyle \frac{j\sqrt{3}}{2}}\\ & =\sqrt{3}{e}^{-\frac{j\pi }{6}}\\ & =\sqrt{6}\sin (t-{\displaystyle \frac{\pi }{6}})\end{array}\end{array}$$