下記の電気回路のY行列を求めよ。
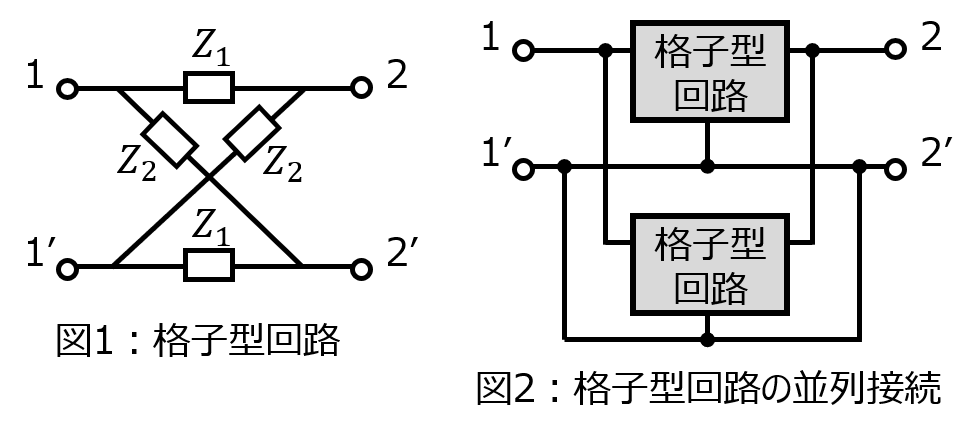
(1)対称格子回路
(2)図1の対称格子回路を2つ並列接続した回路
Y行列とは
二端子対回路において、電流と電圧の入出力関係をアドミタンス行列\(\boldsymbol{Y}\)(下記)を用いて表したものです。
\begin{pmatrix} y_{11} & y_{12} \\ y_{21} & y_{22}\end{pmatrix}
入出力関係は、下記のように表されます。
\begin{aligned}\begin{pmatrix} I_{1} \\ I_{2} \end{pmatrix}=\begin{pmatrix} y_{11} & y_{12} \\ y_{21} & y_{22}\end{pmatrix}\begin{pmatrix} V_{1} \\ V_{2} \end{pmatrix}\end{aligned}
Z行列では、左辺が電圧\(V\)でしたが、Y行列は電流になります。アドミタンスですので、分かりやすいですが、対応関係を覚えておきましょう。
Y行列の求め方
- 端子2を短絡\(V_{2}=0\)し、端子1に電圧源\(V_{1}\)を接続したときに回路に流れる電流\(I_{1},I_{2}\)の関係式を求める。
- 端子1を短絡\(I_{1}=0\)し、端子2に電圧源\(V_{1}\)を接続したときに回路に流れる電流\(I_{1},I_{2}\)の関係式を求める。
- 1.2.で求めた関係式を用い、y行列の具体的な値を求める。
Z行列の場合は端子を開放していましたが、y行列は短絡です。しかし、それ以外に行う計算は同じです。それぞれの行列形式に合わせて式を変形していくのみです。
例題
下記のT型回路のY行列を考えます。
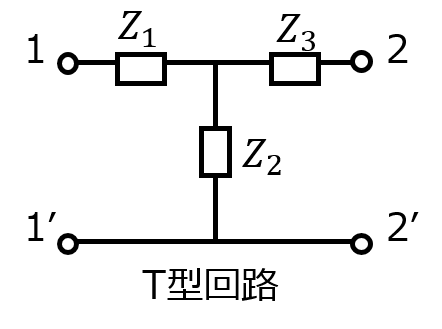
まず、端子2を短絡したときのY行列を考えます。
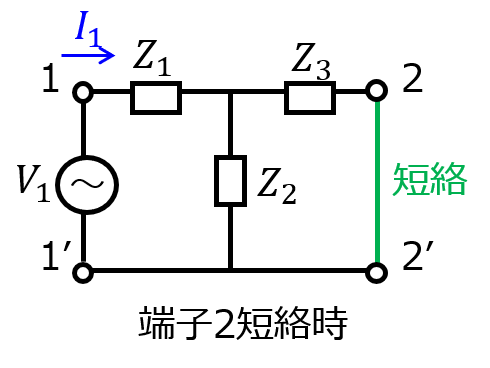
電流\(I_{1}\)は、\(Z_{1}\)を通り、\(Z_{2},Z_{3}\)の並列回路を通ることから
\begin{aligned}V_{1}=\left(Z_{1}+\dfrac{Z_{2}Z_{3}}{Z_{2}+Z_{3}}\right)I_{1}\end{aligned}
これを変形することで
\begin{aligned}I_{1}=\dfrac{Z_{2}+Z_{3}}{Z_{1}Z_{2}+Z_{2}Z_{3}+Z_{1}Z_{3}}\end{aligned}
\(y_{11}\)成分に対応する。
また、電流\(I_{2}\)は、\(I_{1}\)に対し\(Z_{2},Z_{3}\)で分流するから
\begin{aligned}I_{2}&=-\dfrac{Z_{2}}{Z_{2}+Z_{3}} \\ &=-\dfrac{Z_{2}}{Z_{1}Z_{2}+Z_{2}Z_{3}+Z_{1}Z_{3}}\end{aligned}
\(y_{21}\)成分に対応する。
次に、端子1-1’を短絡したときのことを考える。
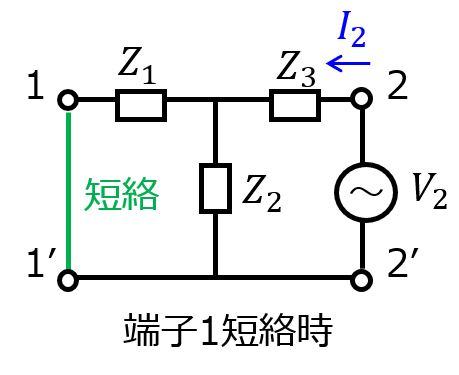
回路の対称性より、(4)式の\(Z_{1}\)と\(Z_{3}\)を入れ替えて
\begin{aligned}I_{2}=\dfrac{Z_{1}+Z_{2}}{Z_{1}Z_{2}+Z_{2}Z_{3}+Z_{1}Z_{3}}V_{2}\end{aligned}
\(y_{22}\)成分に対応する。また、電流\(I_{1}\)は
\begin{aligned}I_{1}&=-\dfrac{Z_{2}}{Z_{1}Z_{2}+Z_{2}Z_{3}+Z_{1}Z_{3}}\end{aligned}
\(y_{12}\)成分に対応する。よって、求めるY行列は
\begin{aligned}\boldsymbol{Y}=\begin{pmatrix}\dfrac{Z_{2}+Z_{3}}{Z_{1}Z_{2}+Z_{2}Z_{3}+Z_{1}Z_{3}} & -\dfrac{Z_{2}}{Z_{1}Z_{2}+Z_{2}Z_{3}+Z_{1}Z_{3}} \\ -\dfrac{Z_{2}}{Z_{1}Z_{2}+Z_{2}Z_{3}+Z_{1}Z_{3}} & \dfrac{Z_{1}+Z_{2}}{Z_{1}Z_{2}+Z_{2}Z_{3}+Z_{1}Z_{3}}\end{pmatrix}\end{aligned}
Y行列の性質
Z行列と似ていますが、一部相違点があります。
- 回路の対称性により、\(y_{12}=y_{21}\)
- Y行列\(\boldsymbol{Y_{1}},\boldsymbol{Y_{2}}\)でそれぞれ示される2端子対回路を並列接続した回路におけるZ行列は\(\boldsymbol{Y_{1}+Y_{2}}\)
- Z行列の逆行列\(\boldsymbol{Z}^{-1}\)はY行列である。
1.について、例題を解いていて気付いたかもしれません。Z行列も同じ性質を持っています。
2.について、Z行列では直列接続時に行列を足し算できました。一方で、Y行列の場合は並列接続時限定です。間違えないようにしましょう。
3.について、(2)式のY行列の逆行列\(Y^{-1}\)を左からかけるとZ行列の式に一致することから説明できます。問題を解くうえで使用することはあまりないですが、知識として持っておきましょう。
解答例
(1)対称格子回路
例題と同じく解いていきます。
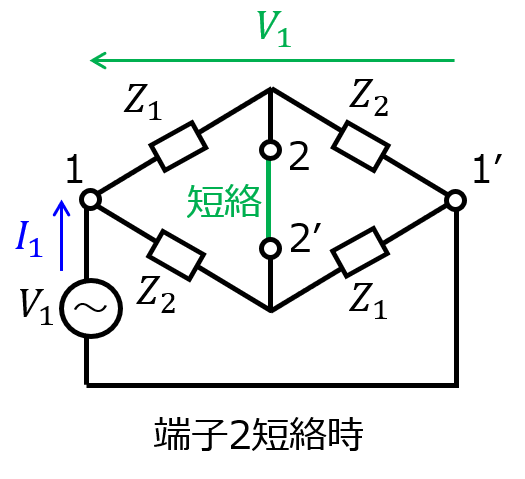
端子2-2’を短絡したとき、回路の合成抵抗を考える。\(Z_{1}\)と\(Z_{2}\)の並列インピーダンス
\begin{aligned}Z=\dfrac{Z_{1}Z_{2}}{Z_{1}+Z_{2}}\end{aligned}
を2つ直列接続したもの\(Z_{total}\)に等しい。
\begin{aligned}Z_{total}=\dfrac{2Z_{1}Z_{2}}{Z_{1}+Z_{2}}\end{aligned}
これを用いると、電流\(I_{1}\)と電圧\(V_{1}\)の関係は
\begin{aligned}V_{1}=\dfrac{2Z_{1}Z_{2}}{Z_{1}+Z_{2}}I_{1}\end{aligned}
\begin{aligned}I_{1}=\dfrac{Z_{1}+Z_{2}}{2Z_{1}Z_{2}}V_{1}\end{aligned}
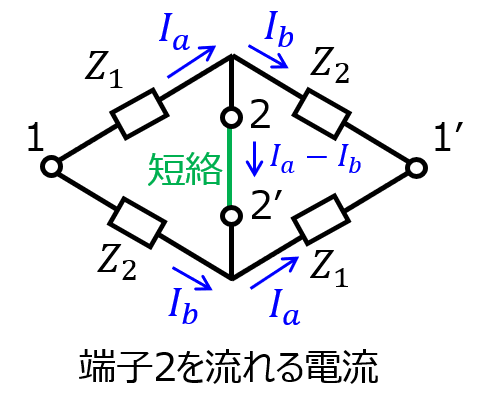
次に、端子2-2’間を流れる電流を考える。分流の考えにより、インピーダンス\(Z_{1}\)に流れる電流\(I_{a}\)とインピーダンス\(Z_{2}\)に流れる電流\(I_{b}\)は下記で表される。
\begin{cases}I_{a}=\dfrac{Z_{2}}{Z_{1}+Z_{2}}I_{1} \\ I_{b}=\dfrac{Z_{1}}{Z_{1}+Z_{2}}I_{1}\end{cases}
端子2-2’間で、\(Z_{1},Z_{2}\)の接続の対応が変わるので
\begin{aligned}I_{2}&=I_{a}-I_{b} \\ &=\dfrac{Z_{1}-Z_{2}}{Z_{1}+Z_{2}}I_{1} \\ &=\dfrac{Z_{1}-Z_{2}}{2Z_{1}Z_{2}}V_{1}\end{aligned}
(12)式、(14)式はそれぞれ\(y_{11},y_{21}\)成分に対応する。
次に、端子1-1’を短絡したときを考える。回路の対称性により
\begin{aligned}y_{11}=y_{22} \\ y_{12}=y_{21}\end{aligned}
以上より、求めるY行列は
\begin{aligned}\boldsymbol{Y}=\begin{pmatrix} \dfrac{Z_{1}+Z_{2}}{2Z_{1}Z_{2}} & \dfrac{Z_{1}-Z_{2}}{2Z_{1}Z_{2}} \\ \dfrac{Z_{1}-Z_{2}}{2Z_{1}Z_{2}} & \dfrac{Z_{1}+Z_{2}}{2Z_{1}Z_{2}}\end{pmatrix}\end{aligned}
(2)並列接続時
Y行列の性質2.より、(1)の結果を2回足し合わせれば良い。
\begin{aligned}\boldsymbol{Y}=\begin{pmatrix} \dfrac{Z_{1}+Z_{2}}{Z_{1}Z_{2}} & \dfrac{Z_{1}-Z_{2}}{Z_{1}Z_{2}} \\ \dfrac{Z_{1}-Z_{2}}{Z_{1}Z_{2}} & \dfrac{Z_{1}+Z_{2}}{Z_{1}Z_{2}}\end{pmatrix}\end{aligned}
最後に
類題が京大の通信情報で出題されたことがあります。知っているだけで満点を狙える内容でしたので、是非ともマスターしましょう。


