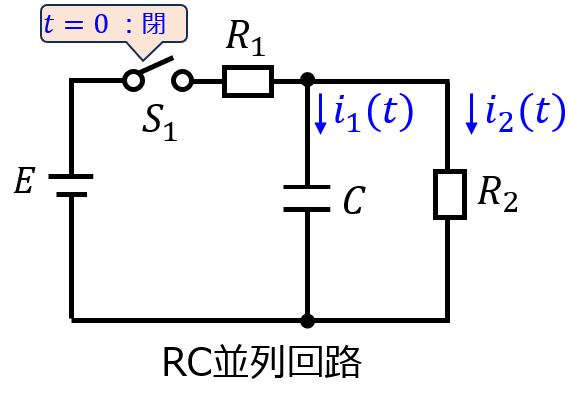
下記のCR回路において、スイッチをt=0で閉じた。下記の問いに答えよ。
(1)コンデンサCに流れる電流\(i_{1}(t)\)を求めよ。
(2)ある時間tにおけるコンデンサに溜まる電荷量\(Q(t)\)を求めよ。
(3)スイッチを閉じて十分時間が経った時にコンデンサに溜まる電荷量\(Q(\infty)\)を求めよ。
電荷量の計算方法
電磁気学と同じく、電流の積分で求められます。過渡現象の場合、exp項に時間変数が付いているので、数Ⅲレベルの積分が必要です。
\begin{aligned}Q(t)=\int^{t}_{0}i(t_{1})dt\end{aligned}
ただ、積分さえできれば、後は他の過渡現象の問題とやることは変わりません。
ジュール熱で問われる場合もありますが、この時も\(Ri(t)^{2}\)で時間関数を求めて積分することで、求めたい時間内のジュール損失が求まります。
解答例
(1)コンデンサに流れる電流
与えられた回路の方程式は下記で表される。
\begin{cases}E_{o}=R_{1}(i_{1}(t)+i_{2}(t))+\dfrac{1}{C}\int i_{1}(t)dt \\ \dfrac{1}{C}\int i_{1}(t)dt=R_{2}i_{2}(t)\end{cases}
これをラプラス変換し
\begin{cases}\dfrac{E_{o}}{s}R_{1}(I_{1}(s)+I_{2}(s))+\dfrac{I_{1}(s)}{Cs} \\ \dfrac{I_{1}(s)}{Cs}=R_{2}I_{2}(s)\end{cases}
上記の第二式より
\begin{aligned}I_{2}=\dfrac{I_{1}(s)}{R_{2}Cs}\end{aligned}
だから、これを第一式に代入して\(i_{1}(t)\)を求める。
\begin{aligned}\dfrac{E_{o}}{s}R_{1}\left(I_{1}(s)+\dfrac{I_{1}(s)}{R_{2}Cs} \right)+\dfrac{I_{1}(s)}{Cs}\end{aligned}
\begin{aligned}I_{1}(s)&=\dfrac{R_{2}CE}{R_{1}R_{2}Cs+R_{1}+R_{2}} \\ &=\dfrac{E}{R_{1}}\dfrac{1}{s+\dfrac{R_{1}+R_{2}}{R_{1}R_{2}C}}\end{aligned}
これをラプラス逆変換すると
\begin{aligned}i_{1}(t)=\dfrac{E}{R_{1}}e^{-\frac{R_{1}+R_{2}}{R_{1}R_{2}C}t}\end{aligned}
(2)コンデンサに溜まる電荷量
(1)の結果を積分すると求められる。
\begin{aligned}Q(t)&=\dfrac{E}{R_{1}}\int^{t}_{0}e^{-\frac{R_{1}+R_{2}}{R_{1}R_{2}C}t_{1}}dt_{1} \\ &=\dfrac{E}{R_{1}}\left(-\dfrac{R_{1}R_{2}C}{R_{1}+R_{2}}\right)\left \lbrack e^{-\frac{R_{1}+R_{2}}{R_{1}R_{2}C}t_{1}} \right \rbrack ^{t}_{0} \\ &=\dfrac{R_{2}EC}{R_{1}+R_{2}}\left(1-e^{-\frac{R_{1}+R_{2}}{R_{1}R_{2}C}t}\right)\end{aligned}
(3)十分時間が経った時の電荷量
(2)の結果において、t→∞の極限を考える。exp項は0になるので
\begin{aligned}Q(\infty)=\dfrac{R_{2}EC}{R_{1}+R_{2}}\end{aligned}
別解
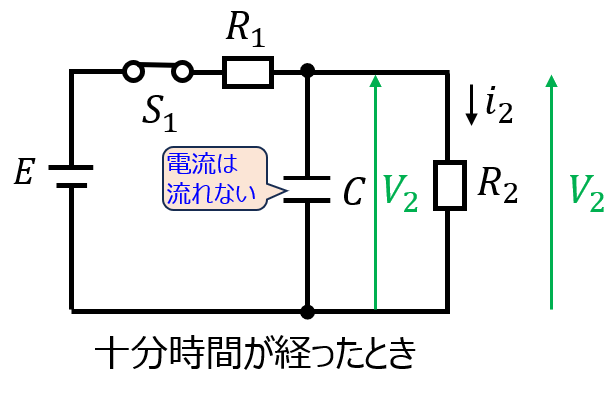
本問においては、問(1)(2)を解かなくても、回路の特性に注目することでも解けます。
十分時間が経ったとき、コンデンサは開放状態となる。並列接続されている\(R_{2}\)にかかる電圧\(V_{2}\)が求まると、\(Q(\infty)=CV\)の関係で電荷量が求まる。
\(V_{2}\)は、抵抗\(R_{1},R_{2}\)の比に依存するので
\begin{aligned}V_{2}=\dfrac{R_{2}}{R_{1}+R_{2}}E\end{aligned}
これより、求める電荷量は
\begin{aligned}Q(\infty)&=CV_{2} \\ &=\dfrac{R_{2}EC}{R_{1}+R_{2}}\end{aligned}
最後に
十分時間が経った時の回路特性を見るだけならば、ラプラス変換により回路方程式が解けていなくても答えにたどり着ける場合があります。また、別解で説明した方法は、会社に入ってから技術的な説明を定性的に行う際に有用です。(実際に、某東証一部企業の入社試験(筆記)でも問われたことが有りました。)
2つの方法で解けるようにしましょう。