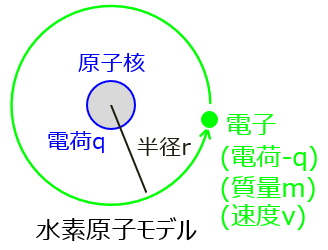
電荷\(q\)の水素原子核の周りを電荷\(-q\)、質量\(m\)の価電子が速度\(v\)、半径\(r\)で円運動しているモデルを考える。ボーアの量子条件の式を下記の式で与えたとき、(1)~(4)に答えよ。
\begin{aligned}rmv=n\hbar\end{aligned}
(1)遠心力とクーロン力のつり合いの式を示せ
(2)ボーアの量子条件の式を用いて、水素原子の半径\(r\)を求めよ。また、基底エネルギーにおける半径はいくらか。
(3)ボーアの量子条件を満足しているとき、電子の運動エネルギー\(K=\frac{1}{2}mv^{2}\)およびポテンシャルエネルギー\(U=-\frac{q^{2}}{4 \pi \varepsilon_{o}r}\)を足した全エネルギー\(E\)に(1)の結果を代入し、\(E\)を\(\varepsilon_{o},h,m,q,n\)で表せ。
(4)ある電子が基底からn=2に励起するために必要なエネルギーを求めよ。
ボーアの量子条件とは
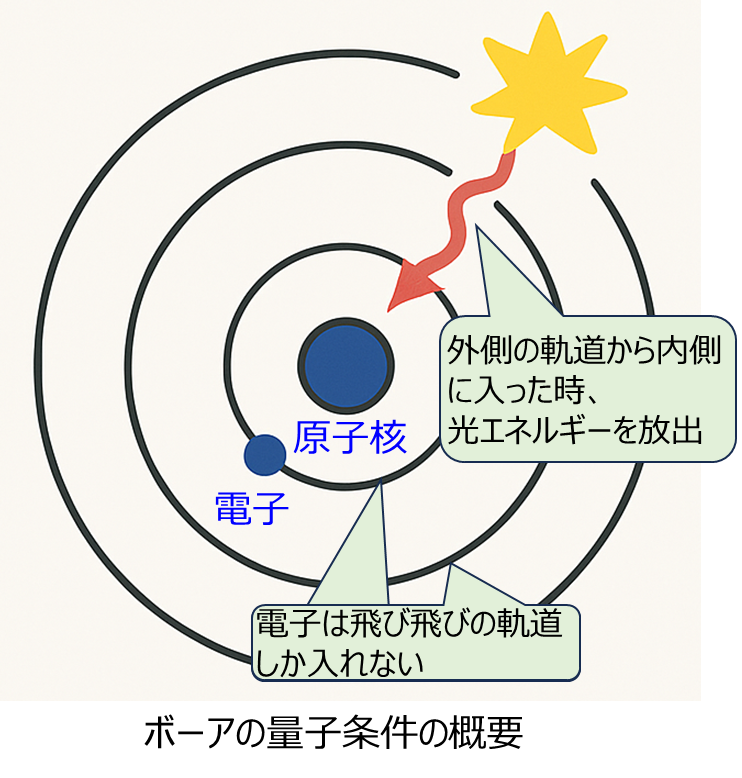
電子は、原子の周りを自由にどこでも飛び回れるわけでは無く、特定の決まった軌道だけ離散的に回ることができる決まり事を言います。問題文で示した式(1)にナンバーnが付いていることからも予想が付きますね。
量子力学の試験だけでなく、半導体デバイスの試験でも問われることがあります。(ドープした不純物が伝導帯へ励起するために必要なエネルギーの計算。などなど・・・)
よく、水素原子モデルを題材にエネルギーの計算に発展させる問題が多いです。どの教科書でも似たようなことが書かれており、作問しやすいこともあります。
本記事では、典型的な問題をまとめてみました。工学部の量子力学の試験と言えば、トンネル効果や井戸型ポテンシャルの透過率を求めるものが多いですが、本問もたまに出てきます。満点狙いなら押さえておきましょう。
解答例
(1)遠心力とクーロン力のつり合い
これは高校物理の知識で解けます。
遠心力は\(F=m\frac{v^{2}}{r}\)、クーロン力は\(F=\frac{q^{2}}{4 \pi \varepsilon_{o}r^{2}}\)なので
\begin{aligned}m\dfrac{v^{2}}{r}=\dfrac{q^{2}}{4 \pi \varepsilon_{o}r^{2}}\end{aligned}
(2)水素原子の半径
(1)式を変形し
\begin{aligned}v=\dfrac{n \hbar}{rm}\end{aligned}
これを問(1)の結果に代入し、\(r\)について整理すると
\begin{aligned}m\dfrac{n^{2} \hbar^{2}}{m^{2}r^{3}}=\dfrac{q^{2}}{4 \pi \varepsilon_{o}r^{2}}\end{aligned}
\begin{aligned}r=\dfrac{n^{2} \hbar^{2}}{m}\cdot\dfrac{4 \pi \varepsilon_{o}}{q^{2}}\end{aligned}
基底エネルギーのとき\(n=1\)なので、このときの半径は
\begin{aligned}r=\dfrac{\hbar^{2}}{m}\cdot\dfrac{4 \pi \varepsilon_{o}}{q^{2}}\end{aligned}
(3)全エネルギーの関係式
全エネルギー\(E\)は、\(E=K+U\)で表されるので
\begin{aligned}E=\dfrac{1}{2}mv^{2}-\dfrac{q^{2}}{4 \pi \varepsilon_{o}r}\end{aligned}
問(1)の結果を上式右辺の第1項に代入して
\begin{aligned}E&=\dfrac{1}{2}m \cdot \dfrac{q^{2}}{4 \pi \varepsilon_{o}r}-\dfrac{q^{2}}{4 \pi \varepsilon_{o}r} \\ &= -\dfrac{q^{2}}{8 \pi \varepsilon_{o}r}\end{aligned}
これに(5)式を代入し
\begin{aligned}E_{n}&=-\dfrac{q^{2}}{8 \pi \varepsilon_{o}}\dfrac{m}{n^{2}\hbar^{2}}\cdot\dfrac{q^{2}}{4 \pi \varepsilon_{o}} \\ &=-\dfrac{mq^{4}}{32 \pi^{2} \varepsilon_{o}^{2} \hbar^{2}}\cdot \dfrac{1}{n^{2}} \end{aligned}
(4)励起に必要なエネルギー
(3)式の結果にn=1,2をそれぞれ代入すると
\begin{cases}E_{1}=-\dfrac{mq^{4}}{32 \pi^{2} \varepsilon_{o}^{2} \hbar^{2}} \\ E_{2}=-\dfrac{mq^{4}}{32 \pi^{2} \varepsilon_{o}^{2} \hbar^{2}}\cdot \dfrac{1}{4}\end{cases}
求めるエネルギーは、\(E_{2}\)と\(E_{1}\)の差を取れば良く
\begin{aligned}E=\dfrac{3}{4} \cdot \dfrac{mq^{4}}{32 \pi^{2} \varepsilon_{o}^{2} \hbar^{2}}\end{aligned}