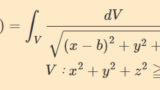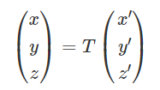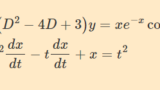数学の科目内容
解析学、線形代数、微分方程式から構成されています。
超難問が出題されるわけではありませんが、幅広く問われます。
名大 電気電子情報通信 院試の全体
基礎科目+専門科目で構成されています。
数学は基礎科目に属します。志望コース共通で、5題中3題選択することが必要です。
標記の分野で大問が分かれていますので、数学だけで3題あります。残り2題は電磁気学(電場)、(磁場)です。
試験時間は180分で、1題当たり60分の配分になります。大学入試同様、時間に余裕があります。
- 解析学 ←本記事で紹介
- 線形代数 ←本記事で紹介
- 微分方程式 ←本記事で紹介
- 電磁気学(電場)
- 電磁気学(磁場)
大問ごとの難易度として、解析学>線形代数>微分方程式(左に行くほど難しい)と思います。
まず、解析学は計算量が多いです。計算ミスが付き物で得点が安定しません。そして、計算方法にも工夫が必要です。
漸化式を導き、積分値を求める問題が頻出ですが、三角関数の式変形などを適切に使用していかないと計算がうまく行きません。1題60分でもしんどいです。
範囲としても、重積分から極限まで幅広く出題されます。併願先の他大で使用しない限り避けた方が無難と考えます。
線形代数は普通です。ランク、固有値、線形独立性の3分野が頻出です。前半は、問題集によくある問題が多く、計算量も少ないので是非得点したいです。
後半は応用問題が出題されますが、他大学と同等の難易度です。他大学で出題されるならば、解析学より優先して選択したいです。線形独立に関する問題が出題されることもありますが、7,8割得点目標です。
微分方程式は、3題の中では一番得点しやすいと思います。小門集合で出題されることが多いので、最初の問題が分からないからと言って全滅になることは無いです。ロンスキアンを利用し、一般解を求める問題が頻出ですので、まず最初に対策したいです。
欠点としては、他大学で出題されることが少なく、併願に向いていないことです。また、級数展開を用いて解を求める応用問題が出題されることがあります。この時は他の大問と同等の難易度になります。
対策に使える参考書、問題集
全体
最近3か年は以下の分野の出題がありました。
- 2023年:
- ロピタルの定理を利用した極限。対数を利用した極限。重積分(極座標変換)。漸化式を利用した三角関数の積分。
- 2次行列の固有値、固有ベクトル。固有値分解を利用した多項式の計算。
- 微分方程式(変数変換型、ロンスキアン型、完全微分方程式型、解が直交する一般解)
- 2022年:
- 多項式の不定積分。n次導関数の算出。重積分。
- 線形独立性。転置行列の固有値、固有ベクトルの算出。
- 微分方程式(変数分離型、変数変換型、ロンスキアン型(2題))
- 2021年:
- 三角関数(sin cos合成)の積分。変数変換を使用した一変数関数の積分。2変数関数の重積分
- パウリ行列(n次)の対角化。多項式の計算。線形独立性
- 微分方程式(変数分離型、完全微分方程式型、ロンスキアン型、級数展開)
解析学は、三角関数に関する積分問題が多いです。問題集などを利用して類題経験を積むと良いです。
線形代数は、冒頭に述べた通り3分野から満遍なく出題されます。
微分方程式は、最後の問題だけ目新しい内容が来ています。(直交、級数展開)
ただ、誘導に乗っていくことで方針は立てやすいです。
解析学
微分積分: 大学院入試問題から学ぶシリーズ 池田和正 (著)
名大の院試レベルと同等の問題が多数収録されています。1,2,3,5章(極限、微分、一変数の積分、重積分)がオススメです。偏微分(極値)と級数展開以外の範囲です。
線形代数
線形代数 (大学院入試問題から学ぶシリーズ) 池田和正 (著)
同じく大学院入試から学ぶシリーズをオススメします。他記事では海老原先生の本を良く紹介していますが、名大院試は、様々な範囲から少し難しいレベルの問題が満遍なく出題されます。いたずらに難しい問題を読み込むのではなく、そこそこのレベルの本を1周した方が良いと考え、上記を選択しました。
微分方程式
微分方程式 技術者のための高等数学 (1) E. クライツィグ (著), Erwin Kreyszig (原名), 近藤 次郎 (翻訳), 北原 和夫 (翻訳), 堀 素夫 (翻訳)
名大のシラバスで紹介されています。元は洋書なので読みにくい印象を受けるかもしれませんが、分かりやすく和訳されていました。順序立って説明しているので、昨今の試験対策書を勉強するより体系立てた理解が出来ます。実際の物理現象と合わせて説明しているので、微分方程式が役立つ場面のイメージも付くと思います。
欠点としては、演習問題に答えが無いことです。このため、下記の本で演習を積むと良いです。
演習微分方程式 (演習数学ライブラリ 新版 3) 寺田 文行 (著), 坂田 ひろし (著)
章の最初には、解法まとめページがあります。これだけでも必見です。
前半の部分を中心に勉強すると良いです。
対策に使える他大学の問題
少し独特な問題もあるので、全てオススメできるわけではないです。実際に確認し、使えると判断した問題を演習すると良いです。
- 解析学:東工大(電気電子系)、京大、広島大、電通大
- 線形代数:東工大(情報通信系)、阪大、電通大
- 微分方程式:東工大(電気電子系)、阪大、神戸大
基本的に、東工大で演習すると良いです。
解析学:京大、電通大は重積分の計算練習に、広島大は極限の計算練習に使えます。
線形代数:阪大は固有値と対角化。電通大は、カーネル(次元)と線形独立性の練習に使えます。
微分方程式:典型問題ばかりなので、どこを選んでも基本大差ないです。阪大には級数展開を利用した問題が出たことがあります。これを確認すると良いかもしれません。
最後に
次回の記事で解説する電磁気学(電場)、(磁場)の2題と微分方程式を本番で3題選択すると、最も得点しやすいのではないかと思います。
解析学、線形代数は保険に取っておく科目選択ができると良いです。