【現代制御】電気回路と状態方程式の算出。状態フィードバックによる極配置

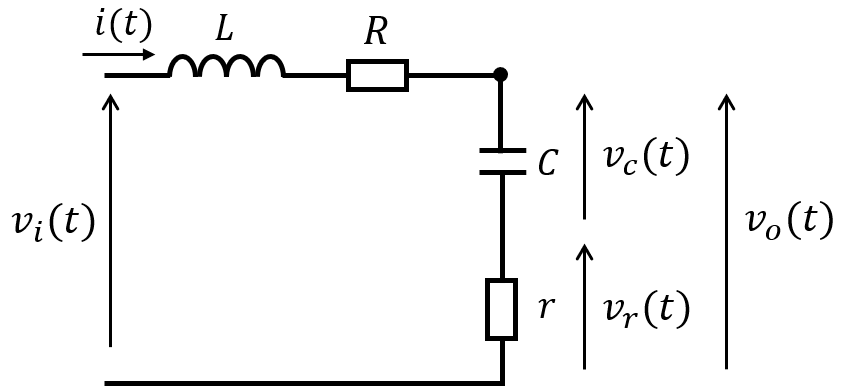
はじめに

本問は、現代制御を院試範囲とする大学でよく出題されます。具体的には、九大、広島大で類題が出題されたことがあります。

古典制御は入力-出力の関係が一対一になっているのでイメージがつきやすいですが、現代制御については、本問のように複数の入出力で成り立っています。

関係式を一つ一つ紐解いていき、状態方程式にする作業が非常に重要になります。

状態方程式とは

あるシステムに対する入力と出力の因果関係を行列表示したものになります。

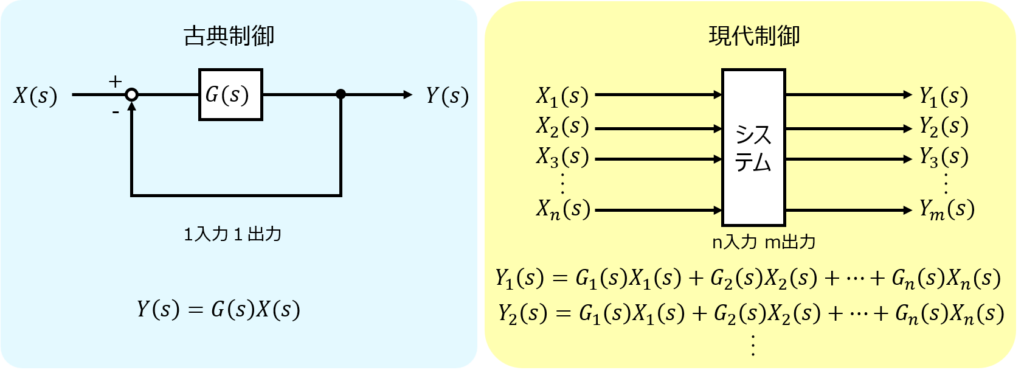
冒頭で述べましたように、古典制御では入出力の関係が一対一だったので、入出力の関係は一つの方程式として書くことができました。

しかし、現代制御では、入出力の変数が複数個あります。

このため、方程式を複数個立式することになります。

このままだと、どの入力がどの出力に対し関係しているのか、式が見にくくなります。

これを解決するため、方程式を行列表示し、入力と出力を分けることで、システムを考えやすくなります。

これを状態方程式と言い、下記のように表すことができます。

\begin{cases}x=Ax+bu\\ y=Cx+du\end{cases}

解答例

(1)状態方程式の立式

まず、回路方程式を立てる。

\begin{cases}v_{i}(t)=L\dfrac{di}{dt}+\left( R+r\right) i\left( t\right) +\dfrac{1}{C}\int i\left( t\right) dt\\ v_{0}(t)=v_{r}(t)+v_{c}\left( t\right) =ri\left( t\right) +\dfrac{1}{C}\int i_{t}dt\\ v_{c}=\dfrac{1}{C}\int i(t) dt\end{cases}

これをtで微分して

\begin{cases}\dot{v_{i}(t)}=\dfrac{1}{L}{vi(t)-(R+r)i(t)-v_{c}(t)} \\ \dot{v_{c}}(t)=\dfrac{1}{C}\end{cases}

以上より、求める状態方程式は

\begin{align}\boldsymbol{A}=\begin{pmatrix} 0 & \dfrac{1}{c} \\ -\dfrac{1}{L} & -\dfrac{R+r}{L} \end{pmatrix} \\ \boldsymbol{b}=\begin{pmatrix} 0 \\ \dfrac{1}{L} \end{pmatrix} \\ \boldsymbol{C}=\begin{pmatrix} 1 & r \\ 0 & r \end{pmatrix} \\ \boldsymbol{d}=\begin{pmatrix} 0 \\ 0 \end{pmatrix}\end{align}

(2)伝達関数の算出

\begin{eqnarray}G\left( s\right) =\boldsymbol{C}\left( s\boldsymbol{I}-\boldsymbol{A}\right) ^{-1}\boldsymbol{b}\end{eqnarray}を計算することで、伝達関数を求められる。

\begin{eqnarray}\left( sI-A\right) =\begin{pmatrix} s & \dfrac{1}{c} \\ -\dfrac{1}{L} & s+\dfrac{R+r}{L} \end{pmatrix} \\ \end{eqnarray}

\begin{eqnarray}\det \left( sI-A\right) =s^{2}+\dfrac{R+r}{L}s+\dfrac{1}{LC}\end{eqnarray}なので

\begin{aligned}G\left( s\right) &=\begin{pmatrix} 1 & r \\ 0 & r \end{pmatrix}\begin{pmatrix} s & -\dfrac{1}{C} \\ \dfrac{1}{L} & s+\dfrac{R+r}{L} \end{pmatrix}\begin{pmatrix} 0 \\ \dfrac{1}{L} \end{pmatrix} \\ &= \dfrac{1}{s^{2}+\dfrac{R+r}{L}s+\dfrac{1}{LC}}\begin{pmatrix} 1 & r \\ 0 & r \end{pmatrix} \begin{pmatrix} s+\dfrac{R+r}{L} & \dfrac{1}{C} \\ -\dfrac{1}{L} & s \end{pmatrix}\begin{pmatrix} 0 \\ \dfrac{1}{L} \end{pmatrix} \\ &= \dfrac{1}{s^{2}+\dfrac{R+r}{L}s+\dfrac{1}{LC}}\begin{pmatrix} \dfrac{1}{LC}+\dfrac{rs}{L} \\ \dfrac{rs}{L}\end{pmatrix} \end{aligned}

出力が2つ存在するので、ベクトル表示です。

(3)可制御性の判定

\begin{eqnarray}Ab=\begin{pmatrix} 0 & \dfrac{1}{C} \\ -\dfrac{1}{L} & -\dfrac{R+r}{L} \end{pmatrix}\begin{pmatrix} 0 \\ \dfrac{1}{2} \end{pmatrix}\end{eqnarray}

だから、可制御性を判定する行列\([b ,Ab]\)について

\begin{pmatrix} 0 & \dfrac{1}{LC} \\ \dfrac{1}{L} & -\dfrac{R+r}{L^{2}} \end{pmatrix}

\(rank=2\)なので、可制御である。

(4)システムの安定性

(2)より、伝達関数の極は、分母に注目し、下記の方程式で求められる。

\begin{eqnarray}s^{2}+\dfrac{R+r}{L}s+\dfrac{1}{LC}=0 \end{eqnarray}

\begin{eqnarray} s=\dfrac{1}{2}\left( -\dfrac{R+r}{L}\pm \sqrt{\left( \dfrac{R+r}{L}\right) ^{2}-\dfrac{4}{LC}}\right ) \end{eqnarray}

これに与えられたパラメータを代入すると

\begin{eqnarray}s=\dfrac{1}{2}\left( 1\pm \dfrac{1}{\sqrt{5}}\right)\end{eqnarray}

\(s>0\)のため、逆ラプラス変換するとexp(t)項の()内は正になる。よって、\(t→∞\)の極限を考えると発散する。

よって、不安定であることが確認できた。

(5)状態フィードバックによる極配置

フィードバックベクトルを導入した時、システムの状態方程式(入力項)をラプラス変換する。

\begin{eqnarray}\dot{x(t)}=\left( A-bf^{t}\right) x\end{eqnarray}なので

\begin{aligned}sI-(A-bf)&=\begin{pmatrix} s & o \\ o & s \end{pmatrix}-\begin{pmatrix} 0 & \dfrac{1}{5} \\ -1 & 1 \end{pmatrix}+\begin{pmatrix} 0 \\ 1 \end{pmatrix}\left( f_{1},f_{2}\right) \\ &=\begin{pmatrix} s & -\frac{1}{5} \\ 1+f_{1} & s-1+f_{2} \end{pmatrix}\end{aligned}

このとき、伝達関数の根は、特性方程式

\begin{aligned}\det \left\{ sI-\left( A-bf^{t}\right) \right\} \\ = s\left( s+f_{2}-1\right) +\dfrac{1}{5}\left( 1+f_{1}\right) \\ =s^{2}+\left( f_{2}-1\right) s+\dfrac{1}{5}\left( 1+f_{1}\right) \end{aligned}

これの極が\(s=-2,-3\)のとき、\begin{eqnarray}\left( s+2\right) \left( s+3\right) =s^{2}+5s+6\end{eqnarray}だから、比較することで

\begin{cases}f_{1}=29\\ f_{2}=6\end{cases}

を得る。

最後に

長丁場な記事となりましたが、いかがでしたでしょうか。

最後の問題まで、院試でよく出てきます。是非、最初から最後まで自力で解けるようになることをオススメします。