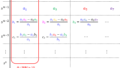
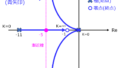
(1)下記のRLC直列回路をラプラス変換し、入力電圧\(V_{i}(s)\)と出力電圧\(V_{o}(s)\)の比の伝達関数\(G(s)\)を求めよ。また、減衰率\(\zeta\)、固有周波数\(\omega_{n}\)を回路定数\(L,R,C\)を用いて表せ。なお、回路定数は抵抗\(R\)、インダクタンス\(L\)、キャパシタンス\(C\)とする。
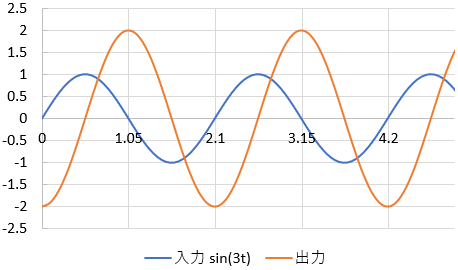
(2)このRLC回路に\(\sin(3t)\)の正弦波を入力したところ、下記の波形になった。また、単位ステップ関数を入力し、十分時間が経過したとき、出力が2になった。伝達関数\(G(s)\)に具体的な数値を与えよ。

2次遅れ要素とは
\(G\left( s\right) =\dfrac{K}{s^{2}+as+b}\)など、分母のsの次数が2次で表される伝達関数のことを言います。
一般的に、システムの伝達関数は下記の形で表すことができます。
\begin{eqnarray}G(s)=\dfrac{b_{0}s^{m}+b_{1}s^{m-1}+ \cdots+b_{m-1}s+b_{m}}{a_{0}s^{n}+a_{1}s^{n-1}+ \cdots+a_{n-1}s+a_{n}}\end{eqnarray}
\(m=0,n=1\)のとき、\(G\left( s\right) =\dfrac{b_{m}}{a_{n-1}s+a_{n}}\)形になり、分母にsの次数が1残ります。このときは1次遅れ要素になります。
「一次遅れ」は-90°位相が遅れることを言います。例えば、上記の伝達関数を\(s→j\omega\)の周波数領域に置き換えると、下記になります。
\begin{eqnarray}G\left( j\omega\right) =\dfrac{b_{m}}{a_{n-1}j\omega+a_{n}}\end{eqnarray}
\(\omega→∞\)の極限を考えると、虚数項が支配的となり、位相が-90°遅れます。これを1次遅れ要素と言います。
この応用で、sの項が2次の時は、位相が-180°遅れます。これを1次の伝達関数に対し2倍位相が遅れますので、2次遅れ要素と言うわけですね。
他、\(G\left( s\right) =\dfrac{b_{m-1}s+b_{m}}{a_{n}}\)のときは、1次進み要素になります。位相が90°進みます。
減衰率と固有周波数
2次遅れ要素が
\begin{eqnarray}G\left( s\right) =\dfrac{\omega _{n}^{2}}{s^{2}+2\xi \omega_{n}s+\omega _{n}^{2}}\end{eqnarray}
で表されるとき、\(\xi\)を減衰率。\(\omega_{n}\)を固有周波数と言います。
減衰率は、入力に対する応答の制動の程度を表します。例として、下記のように、ステップ関数を入力したときの過渡応答を考えます。
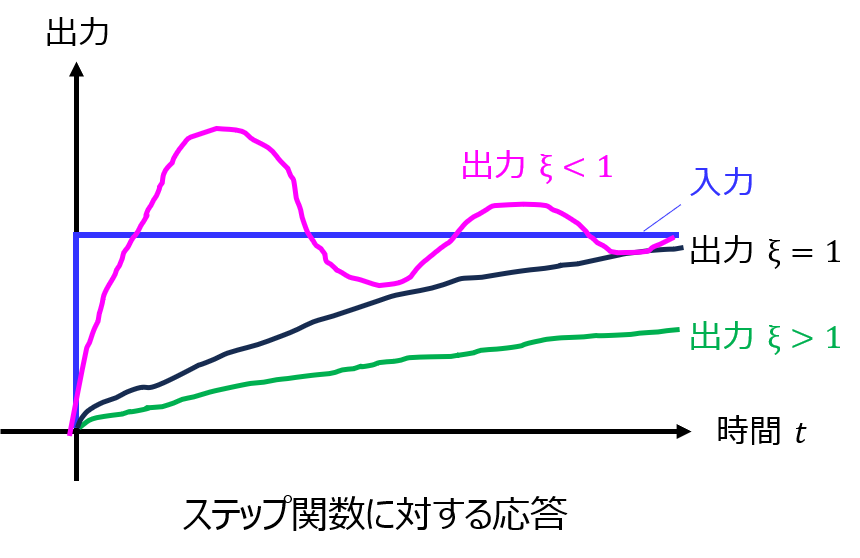
- \(\xi<1\)のときは、応答性は良いが、目標値を超過し、振動しながら減衰していきます。
- \(\xi=1\)のときは、振動せず、入力に対しオンポイントで漸近していきます。
- \(\xi>1\)のときは、過制動となり、目標値に達するまで時間がかかります。
簡単のために、ステップ関数で説明しましたが、問のように正弦波を入力したときは、下記のように伝達関数を推測します。
出力に対する入力の比→減衰率、入力に対する出力の位相遅れ→固有周波数
本問を解くうえでは、上記の知識が非常に重要です。結論、これを覚えているだけで解けます。
解答例
(1)前半 RLC直列回路の伝達関数
回路方程式は、以下のようになる。
\begin{cases}v_{i}(t)\left( t\right) =L\dfrac{di}{dt}+Ri+\dfrac{1}{C}\int _{0}^{\infty }i\left( t\right) dt \\ v_{o}(t)=\dfrac{1}{C}\int _{0}^{\infty }i\left( t\right) dt \end{cases}
これをラプラス変換し、以下の式を得る。
\begin{cases}V\left( s\right) =LsI\left( s\right) +RI\left( s\right) +\dfrac{I\left( s\right) }{Cs} \\ V_{0}\left( s\right) =\dfrac{I\left( s\right) }{Cs} \end{cases}
以上より、伝達関数は下記のように求められる。
\begin{aligned}G(s)&=\dfrac{V_{o}(s)}{V_{i}(s)} \\ &=\dfrac{\dfrac{1}{Cs}}{Ls +R +\dfrac{1}{Cs}} \\ &= \dfrac{1}{LCs^{2}+RCs+1} \\ &=\dfrac{\dfrac{1}{LC}}{s^{2}+\dfrac{R}{L}s+\dfrac{1}{LC}} \end{aligned}
(1)後半 伝達関数の減衰率、固有周波数
(3)式と(6)式の結果を比較して
\begin{eqnarray}\omega_{n}^{2}=\dfrac{1}{LC}, 2\xi\omega_{n}=\dfrac{R}{L}\end{eqnarray}
\begin{eqnarray}\omega_{n}=\dfrac{1}{\sqrt{LC}}, \xi=\dfrac{R}{2}\sqrt{\dfrac{C}{L}}\end{eqnarray}
(2)与えられた波形からの伝達関数の推測
ゲインKを設定し、伝達関数を下記のように置く。
\begin{eqnarray}G\left( s\right) =\dfrac{K \omega _{n}^{2}}{s^{2}+2\xi \omega_{n}s+\omega _{n}^{2}}\end{eqnarray}
ステップ入力に対して十分時間が経った時の出力は2なので、最終値の定理より
\begin{aligned}y\left( t\right) &=\lim _{s\rightarrow 0}s\dfrac{K \omega _{n}^{2}}{s^{2}+2\xi \omega_{n}s+\omega _{n}^{2}}\dfrac{1}{s} \\ K&=2\end{aligned}
また、与えられたグラフは入力に対し、出力が-90°=-π/2の位相差で追従する。
与えられた入力が\(\sin(3t)\)なので、\(s=j\omega\)に対し、\(s=j3\)
このとき、伝達関数は
\begin{eqnarray}\dfrac{2w_{n}^{2}}{-9w^{2}+j2 \xi \omega \omega_{n}w+\omega_{n}^{2}}\end{eqnarray}
-π/2位相差が発生するので、分母の実部は0になる。
\begin{eqnarray}9-\omega^{2}=0 ⇔ \omega_{n}=3\end{eqnarray}
出力波は、出力波に対し2倍になっているので
\begin{eqnarray}\xi=1/2=0.5\end{eqnarray}
以上より、求める伝達関数は
\begin{aligned}G\left( s\right) &=\dfrac{2\cdot 9}{s^{2}+2\cdot \dfrac{1}{2}\cdot 3s+9} \\ &= \dfrac{18}{s^{2}+3s+9} \end{aligned}
最後に
与えられた波形から伝達関数を推測する問題は、院試でよく出題されます。(阪大、九大に多い)
本問で基本的な考え方を示しました。是非、他の波形でも練習してみることをオススメします。