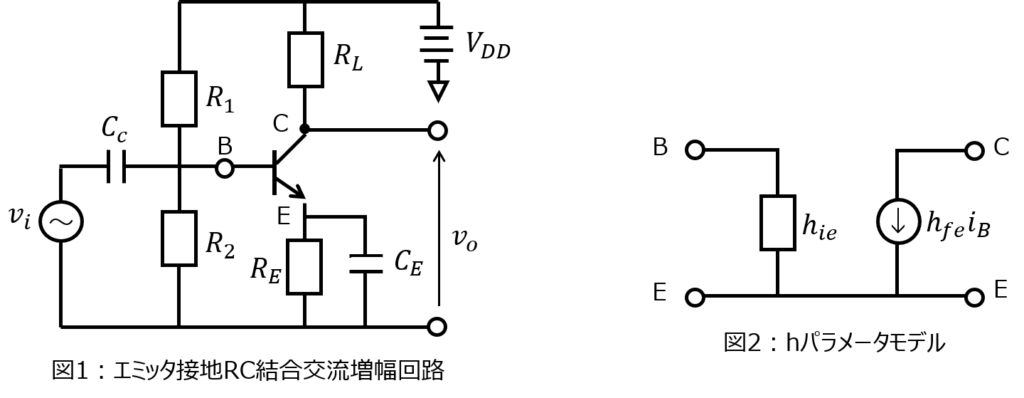
下記のようなnpnバイポーラトランジスタを用いたエミッタ接地RC結合交流増幅回路について考える。
(1)この回路の微小信号等価回路を描け。
(2)中域周波数帯では、\(C_{c},C_{E}\)のリアクタンスを無視することができる。この時の電圧利得を求めよ。
(3)低域周波数帯では、\(C_{c},C_{E}\)のリアクタンスは無視できない。の電圧利得、遮断周波数を求めよ。
バイポーラトランジスタの概要
バイポーラトランジスタは、MOSFETと並ぶ増幅素子です。動作原理は過去の記事でまとめていますが、平たく言えばベースとコレクタに電流を流し、エミッタから増幅した電流が出力される素子になっています。
MOSFETは電圧制御素子に対して、トランジスタは電流制御素子です。
各周波数帯における回路構成の変化
本問は、電子回路にトランジスタを設定したときの増幅特性を考えていきます。特にエミッタ接地型の回路は他の接地方式と比較して院試でよく出てきます。
微小信号等価回路を示し、入力電圧と出力電圧の比を回路方程式を立てて示していけば良いですが、コンデンサのリアクタンスは周波数によって変わります。
よって、周波数帯域によって、実際の回路構成、回路方程式も変わります。
解答例
(1)微小信号等価回路
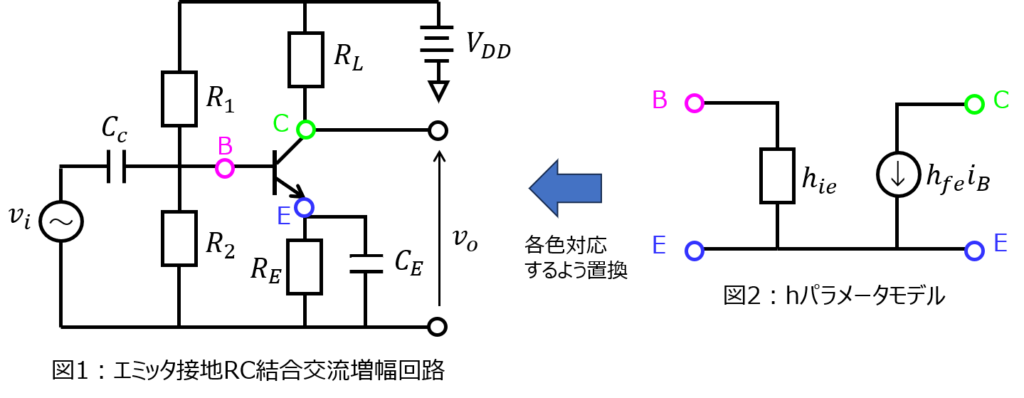
MOSFETの微小信号等価回路の記事でもお話ししたように、非線形素子のトランジスタを与えられた近似モデルのシンボルに置き換えます。
直流成分\(V_{DD}\)は無視できます。よって、\(v_{i}\)のマイナス側の電位と同じとみなしてよいです。
下記の構成になります。
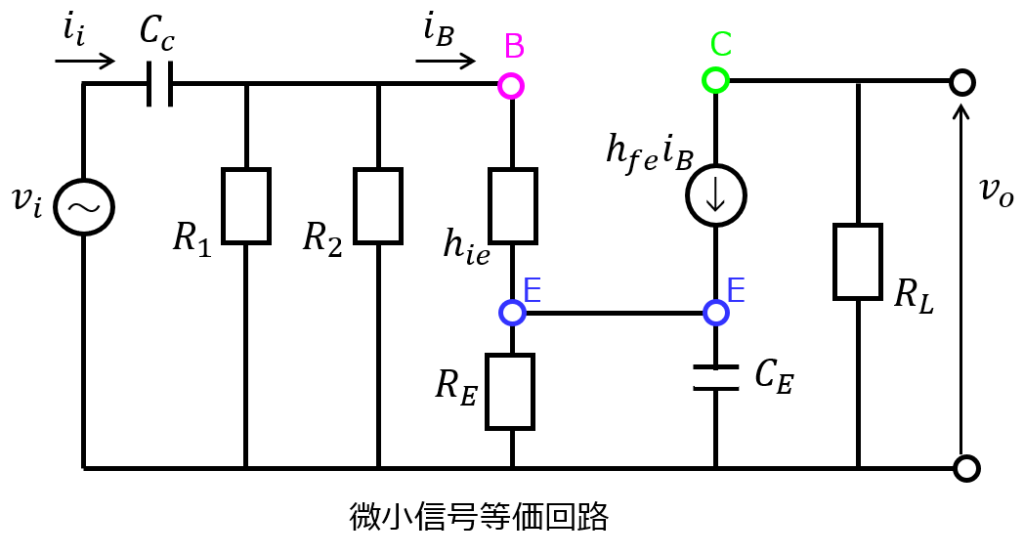
(2)中域周波数帯の電圧利得
コンデンサ成分は無視できるため、下記図の赤枠で囲ったところが短絡されます。
そうなると、電流は\(R_{E}\)を流れなくなります。よって、下記の微小信号等価回路になります。
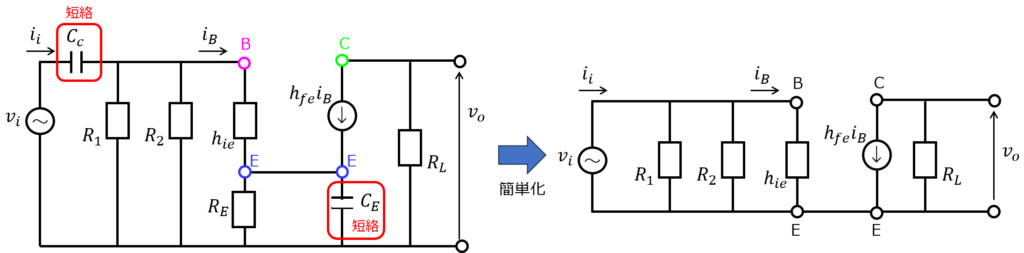
回路方程式を立てていきます。
\begin{cases}v_{i}=h_{ie}i_{B} \\ v_{o}=-R_{L}h_{fe}i_{B}\end{cases}より、\(v_{i}\)と\(v_{o}\)の比を取り、求める電圧利得は
\begin{aligned}K=\dfrac{v_{o}}{v_{i}}=-\dfrac{R_{c}h_{fe}}{h_{ie}}\end{aligned}
(3)低域周波数帯の電圧利得
このときはコンデンサ成分が無視できません。まず、\(C_{E}\)を有限な値とし、\(C_{c}\)を無視した場合を考えます。
下記の回路図となるので、
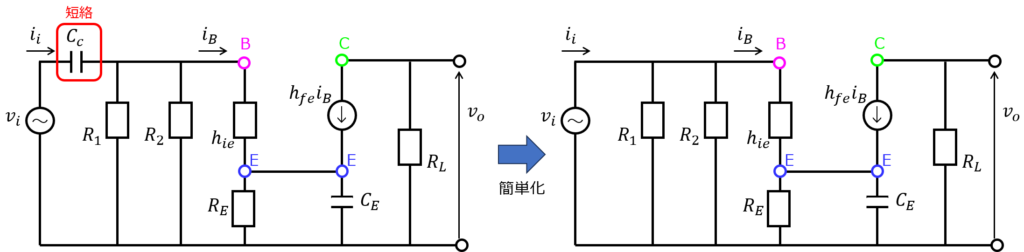
\begin{cases}v_{i}=h_{ie}i_{B}+\dfrac{R_{E}}{1+j\omega C_{E}R_{E}}(1+h_{fe})i_{B} \\ v_{o}=-R_{L}h_{fe}i_{B}\end{cases}
求める電圧利得は、
\begin{aligned}K=\dfrac{v_{o}}{v_{i}}&=-\dfrac{R_{L}h_{fe}}{h_{ie}+\frac{R_{E}(1+h_{fe})}{\omega C_{E}R_{E}}} \\ &=-\dfrac{R_{L}h_{fe}}{h_{ie}}\dfrac{1}{1-j\frac{R_{E}(1+h_{fe})}{\omega C_{E}R_{E}}}\end{aligned}
以上より、遮断周波数は、\(f=\dfrac{C_{E}R_{R}}{2 \pi R_{E}(1+h_{fe})}\)
(4)低域周波数帯の電圧利得
次に、\(C_{c}\)を有限な値とし、\(C_{E}\)を無視した場合を考えます。
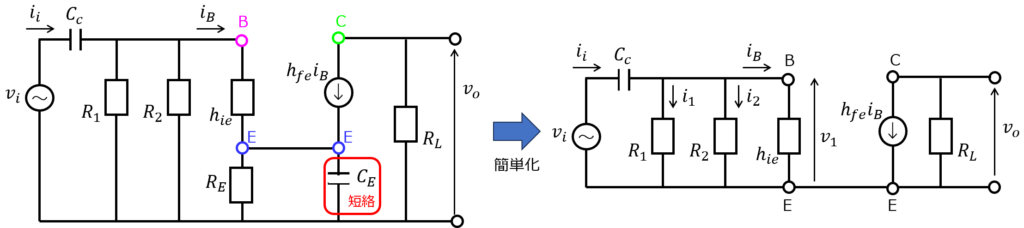
入力端に\(C_{c}\)が付いているので、\(v_{i}\)の求め方が少し難しくなります。
今まで、バイポーラトランジスタでの電圧降下\(h_{ie}i_{B}\)を考えていれば、それが\(v_{i}\)と等しかったですが、今度は\(C_{c}\)分の電圧降下を足さなければなりません。
しかも、\(R_{1},R_{2}\)にも電流が流れるので、\(i_{B}\)をそのまま\(C_{c}\)のリアクタンスと掛け合わせるわけにもいきません。
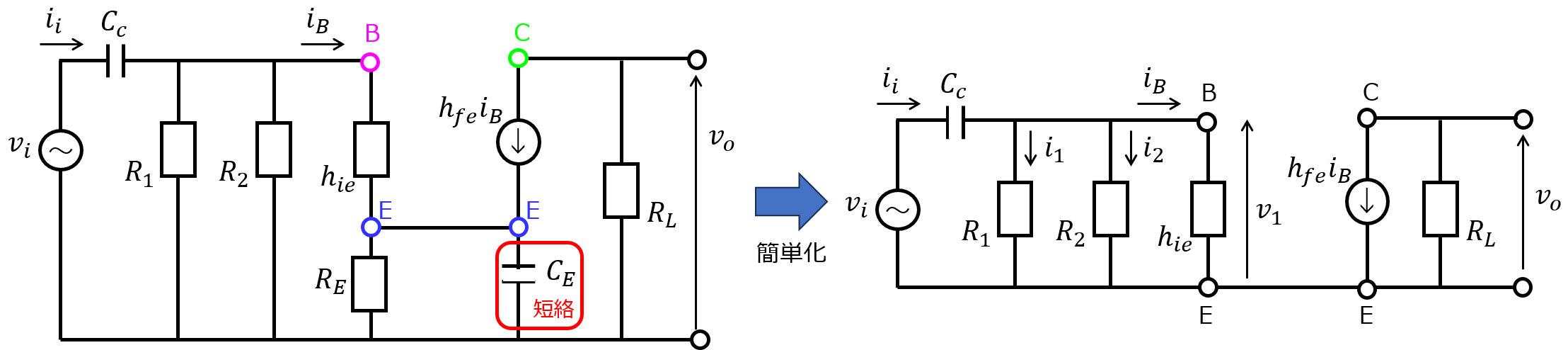
解法ですが、まず、\(C_{c}\)より右にかかる電圧を\(v_{1}\)と置きます。
\(R_{1},R_{2}\)に流れる電流を\(i_{1},i_{2}\)とすると、
\begin{aligned}i_{1}=\dfrac{v_{1}}{R_{1}},i_{2}=\dfrac{v_{1}}{R_{2}}\end{aligned}と求められます。
\begin{aligned}v_{1}=h_{ie}i_{B} , i_{i}=i_{1}+i_{2}+i_{B}\end{aligned}なので
\begin{aligned}i_{i}=\dfrac{h_{ie}i_{B}}{R_{1}}+\dfrac{h_{ie}i_{B}}{R_{2}}+i_{B}\end{aligned}になります。
よって、\begin{aligned}v_{i}=\dfrac{i_{B}}{j \omega C_{c}}(\dfrac{h_{ie}}{R_{1}}+\dfrac{h_{ie}}{R_{2}}+1)\end{aligned}
で、\(v_{o}=v_{o}=-R_{L}h_{fe}i_{B}\)なので、求める利得は
\begin{aligned}K=-\dfrac{R_{L}h_{fe}}{h_{ie}}\dfrac{1}{1+\frac{1}{j \omega C_{c} h_{ie}}(\dfrac{h_{ie}}{R_{1}}+\dfrac{h_{ie}}{R_{2}}+1)}\end{aligned}
よって、遮断周波数は、\(f=\dfrac{C_{c}h_{ie}}{2 \pi(\dfrac{h_{ie}}{R_{1}}+\dfrac{h_{ie}}{R_{2}}+1)}\)
\(\omega = 0\)だと分母が∞になるため、利得は0です。
中域周波数帯に近づくほど、利得が増加していき、やがて(2)の答え\(K=\dfrac{v_{o}}{v_{i}}=-\dfrac{R_{c}h_{fe}}{h_{ie}}\)に落ち着きます。
補足
仮にコンデンサ成分が無い場合、常時中域周波数帯の利得になります。これだけ見るとコンデンサが無い方が良いようにも見えます。
では、なぜコンデンサを入れるのでしょうか。答えは次回の記事にて説明します。
最後に
MOSFETと同様、バイポーラトランジスタの周波数特性を求める問題は院試頻出です。
本問を通して練習していきましょう。