(1)下記のダーリントン回路(2段)について考える。上段に記載しているトランジスタを1、下段に接続しているトランジスタを2とする。エミッタ接地の電流増幅率をそれぞれ\(\beta_{1},\beta_{2}\)とする。トランジスタ2のコレクタ、エミッタに流れる電流値\(I_{c1},I_{e2}\)を、\(I_{B1},\beta_{1},\beta_{2}\)を用いて表せ。
(2)ダーリントン回路を多段接続するときに注意点と対策を述べよ。
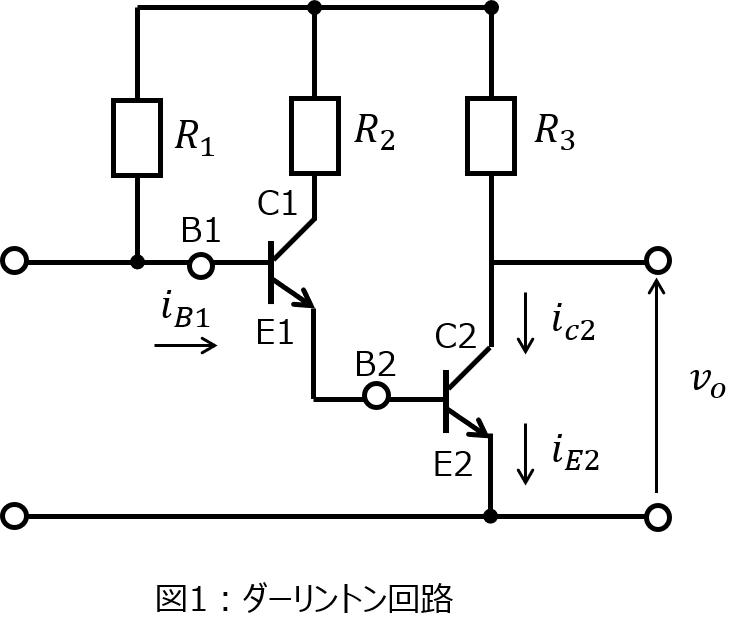
ダーリントン回路について
トランジスタ(またはMOSFET)をエミッタ接地(ソース接地)で多段接続し、電流利得を大きくした回路です。
電流利得について、エミッタ電流増幅率を\(\beta\)とすると、接続した段数分だけ乗算して増えていきます。これを、問(1)を解くことで見ていきましょう。
(1)電流値
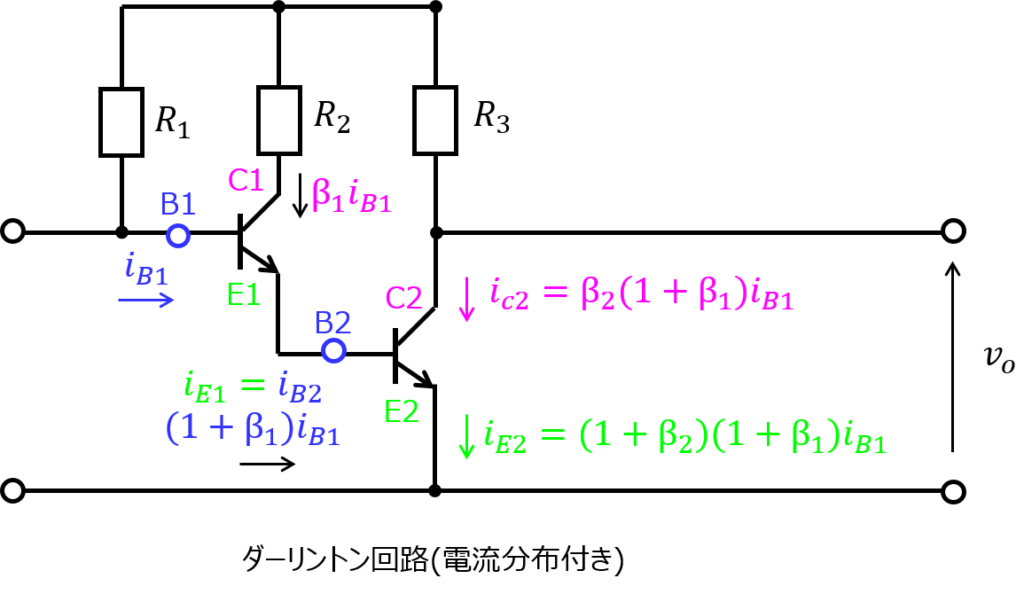
上段から順にトランジスタの各素子に流れる電流値を求めていきます。
エミッタ電流増幅率の定義より、トランジスタ1のコレクタに流れる電流\(I_{c1}\)は
\begin{aligned}I_{c1}=\beta_{1}I_{B1}\end{aligned}
\(I_{E}=I_{B}+I_{C}\)より
\begin{aligned}I_{E1}=I_{B2}=(1+\beta_{1})I_{b1}\end{aligned}
トランジスタ2についても同様にして
\begin{cases}I_{c2}=\beta_{2}(1+\beta_{1})I_{B1} \\ I_{E2}=(1+\beta_{2})(1+\beta_{1})I_{B1}\end{cases}
\(1+\beta_{1}≒\beta_{1} , 1+\beta_{2}=\beta_{2}\)なので、
\begin{aligned}I_{E2}=\beta_{1}\beta_{2}I_{B1}\end{aligned}
\(\beta_{1}\beta_{2}\)倍に電流を増幅できていることが分かる。
(2)多段接続するときの注意点
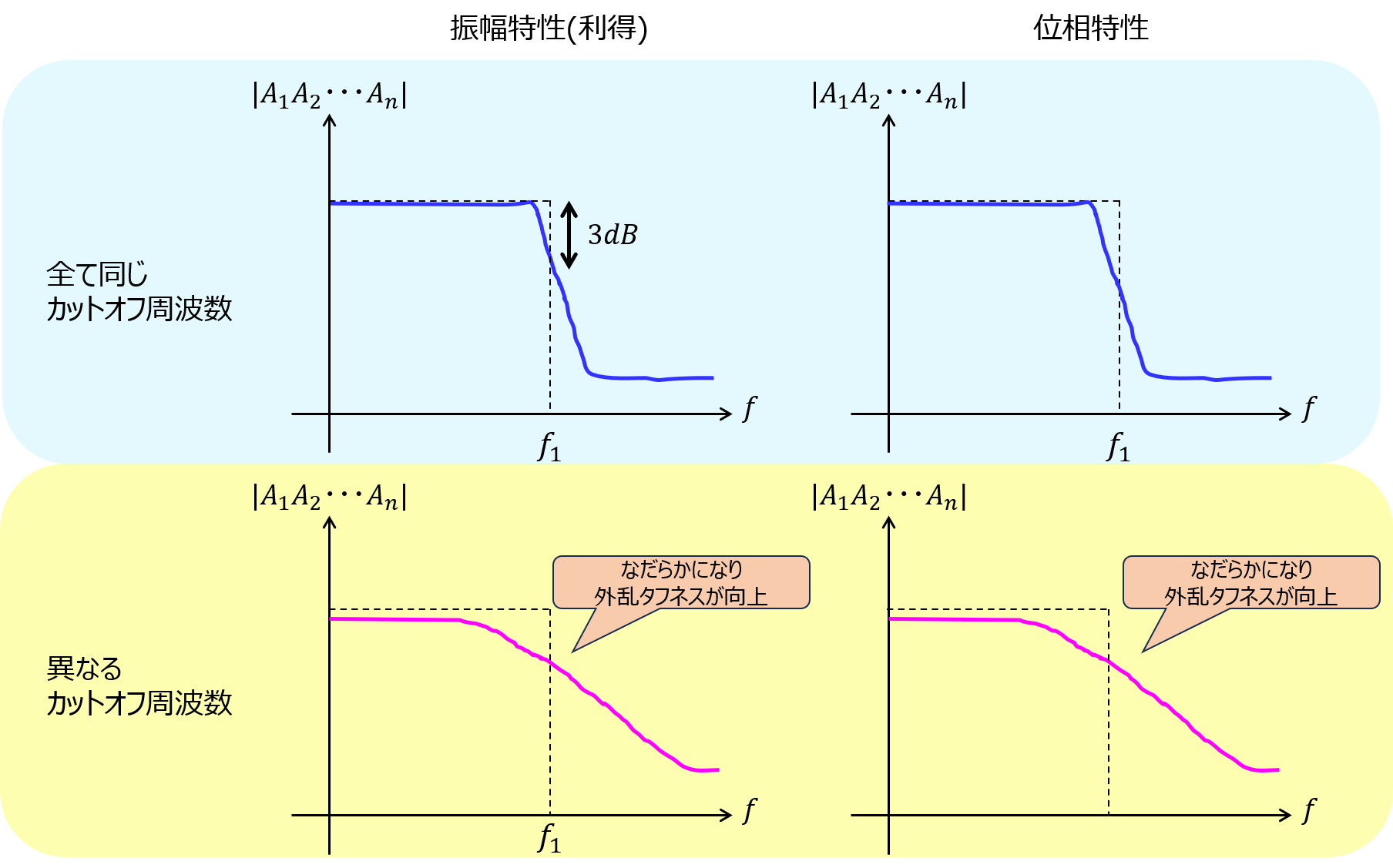
【注意点】カットオフ周波数付近で運転したとき、外乱による周波数変動で電圧利得が急変動し、出力信号のレベルが不安定になりやすい。
【対策】多段接続するトランジスタのそれぞれのカットオフ周波数は、なるべくずらして設計する。
ダーリントン回路は、一般的にエミッタ接地で動作させます。すると、どうなるでしょうか。
カスコード回路の記事で説明したように、ミラー効果が発生します。これにより、ある周波数帯以上だと、利得が低下してしまいます。
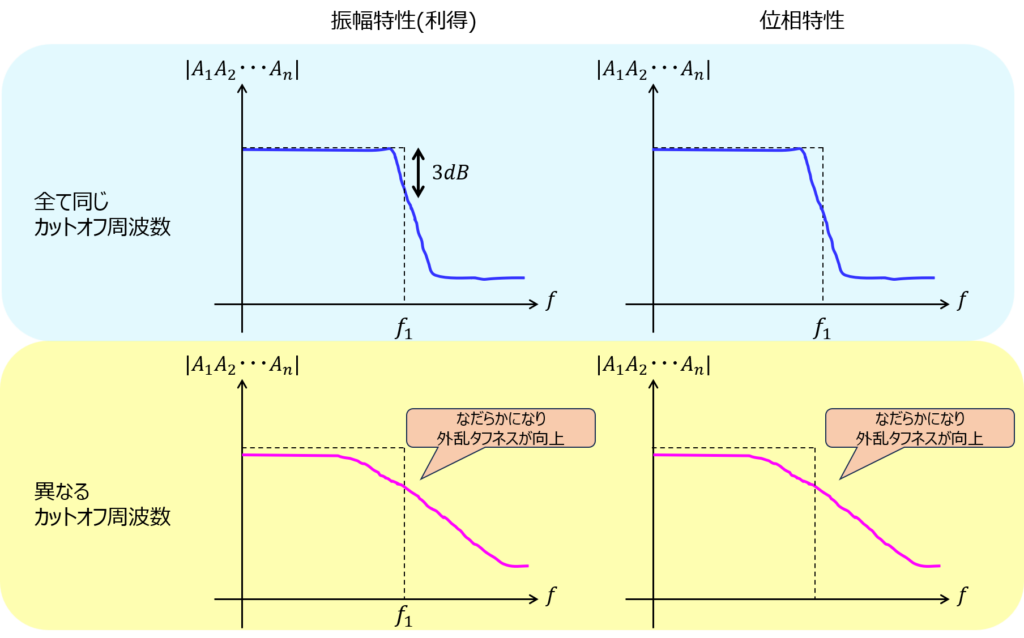
多段接続するトランジスタが全て同じ特性だと、ある周波数に差し掛かった時、同じタイミングで急激に利得が低下します。(振幅特性)
また、振幅が十分減衰しない領域で位相回転が大きい場合、回路の発振が発生する可能性があります。(位相特性)
各トランジスタ\(i\)の利得を\(A_{i}\)、カットオフ周波数を\(f_{i}\)とすると、回路全体の利得\(A_{T}\)は下記になります。
\begin{aligned}A_{T}=\dfrac{A_{1},A_{2} \cdots A_{n}}{\left( 1+j\dfrac{f}{f_{1}}\right) \left( 1+j\dfrac{f}{f_{2}}\right) \ldots \left( 1+j\dfrac{f}{f_{n}}\right) }\end{aligned}
\(f_{1}=f_{2}= \cdots = f_{n}\)のとき、同じ周波数で分母の虚数項が支配的になるので、利得は大きく減衰します。数式でも証明できました。
これを防ぐために、特性が異なるトランジスタを組み合わせれば、\(f_{1}=f_{2} \cdots\)の等号は成立せず、減衰する利得を抑えられるわけですね。
最後に
ダーリントン回路は、北大で出題されたことがあります。他の回路と異なり、小信号等価回路を作成することは少ないので、電流増幅率に応じて地道に計算することが求められます。