院試でよく出るフーリエ変換の証明問題

フーリエ変換とは

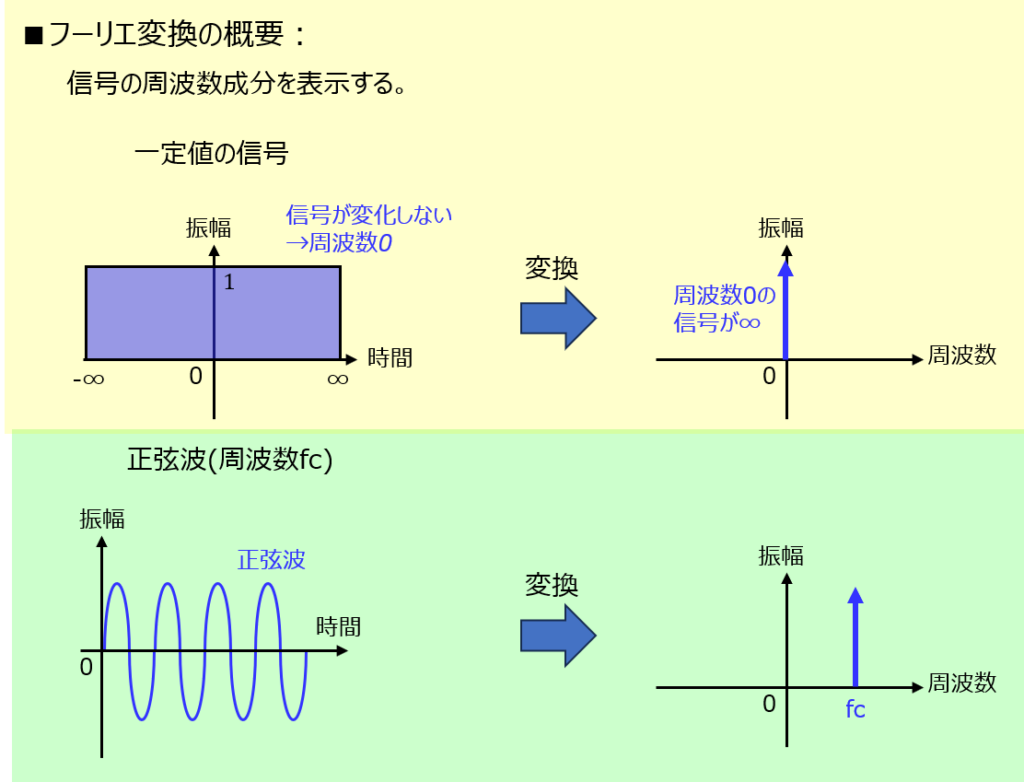
時間領域\(t\)の関数\(f(t)\)を、下記のように周波数領域\(F(\omega)\)に変換することを言います。

\begin{aligned}F(\omega)=\int _{-\infty }^{\infty } f\left( t\right) e^{-j \omega t} dt \end{aligned}

これにより、\(f(t)\)の持っている周波数成分を抽出することができます。

産業界では、信号処理、非破壊検査など、様々な用途に使用されています。

フーリエ変換を出題する大学

特に、東大、阪大の院試ではフーリエ変換の性質の証明問題が出題されます。

本記事では、どの教科書でも紹介される事項からやや発展的なものまで、院試で問われやすい関係式、性質を下記に紹介していきます。

フーリエ変換の性質

性質1 フーリエ変換が可能である必要十分条件

絶対積分可能であることです。

常識と思うかもしれませんが、実際に東大電気系の問1で出題されたことがあります。侮れません。

数式として表すと下記になります。

\begin{aligned}\int _{-\infty }^{\infty }\left| f\left( t\right) \right| dt <\infty\end{aligned}

十分性は下記になります。

\(\int _{-\infty }^{\infty }\left| f\left( t\right) \right| dt \)が有限ならば、\(|e^{j\omega t}|=1\)より

\begin{aligned}\int _{-\infty }^{\infty }\left| f\left( t\right) \right| dt = \int _{-\infty }^{\infty }\left| f\left( t\right) e^{j\omega t} \right| dt \end{aligned}

だから、

\(\int _{-\infty }^{\infty } f\left( t\right) e^{-j \omega t} dt\)も有限である。

性質2 \(F(\omega)=R(\omega)+jX(\omega)\)の性質

\(F(\omega)\)を実部\(R(\omega)\)、虚部\(X(\omega)\)に分けると、下記の関係式が成立します。

\begin{cases}R(\omega)=\int _{-\infty }^{\infty }f(t)\cos\omega t dt \\ X(\omega)=-\int _{-\infty }^{\infty } f(t)\sin\omega t dt \\ R(\omega)=R(-\omega) \\ X(\omega)=-X(\omega)\end{cases}

証明

オイラーの公式より、\(e^{-j\omega t}=\cos\omega t -j \sin\omega t\)なので

\begin{aligned}F(\omega)=\int _{-\infty }^{\infty } f\left( t\right) e^{-j \omega t} dt = \int _{-\infty }^{\infty } f\left( t\right) (\cos \omega t-j\sin\omega t)dt=R(\omega)+jX(\omega)\end{aligned}

\(e^{j\omega t}=\cos\omega t +j \sin\omega t\)で、虚部の符号が変わるので

\begin{cases}R(\omega)=R(-\omega) \\ X(\omega)=-X(\omega)\end{cases}

上記の証明より、共役複素数\(F^{*}(\omega)\)について

\begin{aligned}F^{*}(\omega)=R(-\omega)+jX(-\omega)=F(-\omega)\end{aligned}

も成立します。

補足

\(R(\omega)\)をフーリエ余弦変換。\(X(\omega)\)をフーリエ正弦変換と言います。

\(f(t)\)が偶関数なら、実部の項のみ残るので初めから\(R(\omega)\)だけ考えれば良く
\(f(t)\)が奇関数なら、逆に虚部の項\(X(\omega)\)のみ考えれば良いです。

性質3 比例推移 \(F[f(t-t_{0})]=F(\omega)e^{-j\omega t_{0}}\)

証明

\(F[f(t-t_{0})]=\int _{-\infty }^{\infty } f\left( t-t_{0}\right) e^{-j \omega t}\)について、

\(t-t_{0}=x\)の変数変換を行うことで

\begin{aligned}F[f(t-t_{0})]=e^{-j\omega t_{0}}\int _{-\infty }^{\infty } f\left( t\right) e^{-j \omega t}=F(\omega)e^{-j\omega t_{0}}\end{aligned}

補足

同じ考え方で、周波数領域に対しての比例推移も成立します。

\begin{aligned}F[f(t-t_{0})e^{j\omega_{0}t}]=F(\omega-\omega_{0})\end{aligned}

性質4 \(F[F(t)]=2 \pi f(-\omega)\)

ある関数\(f(t)\)をフーリエ変換した関数\(F(\omega)\)をもう一度フーリエ変換すると、フーリエ変換前の関数の正負が反転した状態になる。ことを示しています。

この性質、試験で意外と出てきます。

知識として持っておくと、証明したときの計算ミスに気付くことができます。

証明

フーリエ逆変換の公式を用いる。

\begin{aligned}f(t)=\dfrac{1}{2\pi}\int^{\infty}_{-\infty}F(\omega)e^{j\omega t} d\omega\end{aligned}

だから、

\begin{aligned}2\pi f(t)=\int^{\infty}_{-\infty}F(\omega)e^{j\omega t} d\omega\end{aligned}

\(t\)を\(-t\)に置き換えると

\begin{aligned}2\pi f(-t)=\int^{\infty}_{-\infty}F(\omega)e^{-j\omega t} d\omega\end{aligned}

tを\(\omega\)に置き換えると

\begin{aligned}2\pi f(-\omega)=\int^{\infty}_{-\infty}F(t)e^{-j\omega t} dt =F[F(t)]\end{aligned}

性質5 \(F[f'(t)]=j\omega F(\omega)\) (※\(f(0)=0,f(±\infty)=0)\)

これは、院試でよく出るラプラス変換の公式の記事でも説明しました。

\(s\)を\(j \omega\)に置き換えれば良いので、気づきやすいかもしれません。

証明

部分積分より

\begin{aligned}F[f'(t)]&=\int _{-\infty }^{\infty } f’\left( t\right) e^{-j \omega t}dt \\ &= \left[f(t)e^{-j\omega t} \right]^{\infty}_{\infty}+j \omega \int _{-\infty }^{\infty } f\left( t\right) e^{-j \omega t}dt \\ &= j\omega F(\omega) \end{aligned}

性質6 畳み込み積分のフーリエ変換

証明問題としての出題は少ないですが、知識としては必要です。

ある関数\(f_{1}(t),f_{2}(t)\)の畳み込み積分の記号を\(*\)とすると

\begin{aligned}F[f_{1}(t)*f_{2}(t)]=F_{1}(\omega)F_{2}(\omega)\end{aligned}

周波数領域で考えると、積分を省略できることが分かりました。

これは、信号処理のシステムでよく使用します。

時間領域で入出力を考えると、人間の手で計算することは大変だから、周波数領域で考える。と言うことですね。

性質7 パーシバルの公式

\begin{aligned}\int _{-\infty }^{\infty }\left| f\left( t\right) \right|^{2} dt = \dfrac{1}{2 \pi}\int _{-\infty }^{\infty }\left| F\left( \omega \right) \right|^{2} d\omega \end{aligned}

が成立します。

一例として、信号\(f(t)\)の消費電力を求める時によく使います。

\(f(t)\)自体は、式が複雑で人間の手で積分が難しいとき、\(F(\omega)\)の2乗を積分して2πを割ることで求めることがあります。

\(|F(\omega)|^{2}=F(\omega)F^{*}(\omega)\)ですので、共役複素数を取るとさらに式を簡単にした状態で積分できます。

参考文献

H.P. スウ(著)、佐藤 平八(訳) フーリエ解析 工学基礎演習シリーズ1 第4章

※本書に限らず、外国の本は定理の証明が豊富なため、証明問題の多い大学院を受ける際は参考にした方が良いかもしれません。