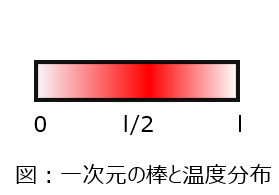
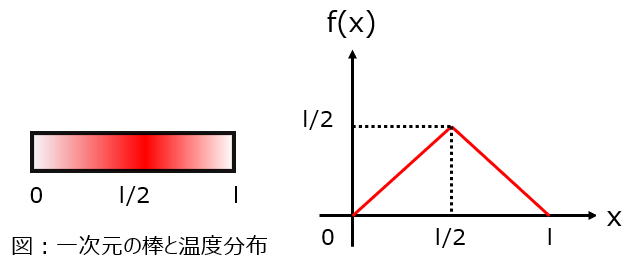
長さlの一次元の棒の初期温度が下記のように与えられている
\begin{aligned}f(x)=\begin{cases}x \qquad (0<x<l/2) \\ l-x \quad (l/2<x<l)\end{cases}\end{aligned}
このとき、時間t経過後の位置xにおける温度分布\(u(x,t)\)を求めよ。なお、熱伝導方程式は以下のように与えられる。
\begin{aligned}\Delta u(x,t)-\dfrac{1}{c^{2}}\dfrac{\partial u}{\partial t}=0\end{aligned}
ここで、\(\lambda,\rho,\sigma\)は、それぞれ導体の熱伝導率、密度、比熱とし、\(c^{2}=\frac{\lambda}{\rho \sigma}\)とする。
はじめに
今までの記事でちょくちょく出てきましたが、偏微分方程式はフーリエ級数、変換、ラプラス変換を利用すると手計算で求められる場合があります。
院試でも、京大(情報学研究科)の先端情報専攻で出題されることがあります。
本記事では、フーリエ級数を用いて熱伝導方程式を解いてみます。
解答例
まず、一般解を求めた後、境界条件に基づく特殊解を求める順序で進めていきます。
一般解の求め方
\(u(x,t)=X(x)T(t)\)と変数分離をする。(2)式に代入すると
\begin{aligned}X^{\prime \prime}(x)T(t)-\dfrac{1}{c^{2}}X(x)T^{\prime}(t)=0\end{aligned}
両辺\(X(x)T(t)\)で割ると
\begin{aligned}\dfrac{X^{\prime \prime}(x)}{X(x)}=\dfrac{1}{c^{2}}\dfrac{T^{ \prime}(t)}{T(t)}\end{aligned}
左辺はxのみの関数で、右辺はtのみの関数なので、それぞれの結果は定数\(K\)になる。\(K=±k^{2}\)とし、それぞれの場合の一般解を考える。
(i)Kが正(\(+k^{2}\))のとき
\begin{aligned}X^{\prime \prime}(x)-k^{2}X(x)=0\end{aligned}
より、一般解は
\begin{aligned}X(x)=Ae^{kx}+Be^{-kx}\end{aligned}
境界条件\(u(x=0,t)=0\)を考えると、A=-B=0。このとき、任意の点で\(X(x)=0\)になるため不適
(ii)Kが負(\(-k^{2}\))のとき
\begin{aligned}X^{\prime \prime}(x)+k^{2}X(x)=0 \\ T^{\prime}(t)+c^{2}k^{2}T(t)=0\end{aligned}
\(e^{at}\)型の一般解を想定することで
\begin{cases}X(x)=A\cos kx+B\sin kx \\ T(t)=Ce^{-c^{2}k^{2}t}\end{cases}
境界条件\(u(x=0,t)=0,u(x=l,t)=0\)を考えると、
\begin{cases}X(0)=A=0 \\ X(l)=B \sin kl=0\end{cases}
以上より、自然数\(n\)を用いて、\(k=\dfrac{n\pi}{l}\)
\begin{cases}X_{n}(x)=B_{n}\sin \dfrac{n \pi x}{l} \\ T(t)=C_{n}^{-c^{2}k^{2}t}=C_{n}e^{\frac{-c^{2}n^{2}\pi^{2}t}{l^{2}}}\end{cases}
になるので、求める一般解\(u(x,t)=X(x)T(t)\)は
\begin{aligned}u_{n}(x,t)=B_{n}C_{n}e^{\frac{-c^{2}n^{2}\pi^{2}t}{l^{2}}}\sin\dfrac{n \pi x}{l}\end{aligned}
特殊解の求め方
初期条件を満たすため、(10)式を用いて下記のような級数を考える。
\begin{aligned}u_{n}(x,t)=\sum^{\infty}_{n=1}B_{n}C_{n}e^{\frac{-c^{2}n^{2}\pi^{2}t}{l^{2}}}\sin\dfrac{n \pi x}{l}\end{aligned}
(1)式が初期条件として与えられているので
\begin{aligned}u(x,0)&=f(x) \\ &=\sum^{\infty}_{n=1}B_{n}C_{n}e^{\frac{-c^{2}n^{2}\pi^{2}t}{l^{2}}}\end{aligned}
\(B_{n}C_{n}\)は、\(f(x)\)のフーリエ正弦級数となるように選ぶ必要があるので
\begin{aligned}B_{n}C_{n}&=\dfrac{2}{l}\int^{l}_{0}f(x)\sin \dfrac{n \pi x}{l}dx \\ &=\begin{cases}0 \qquad n=2,4,6… \\ \dfrac{4l}{n^{2}\pi^{2}} \quad n=1,5,9… \\ -\dfrac{4l}{n^{2}\pi^{2}} \quad n=3,7,11…\end{cases}\end{aligned}
これを(10)式に代入することで特殊解を得る。
参考
2次元の偏微分方程式(境界値問題)については、導波管(電磁波工学)を題材に解いている記事が有ります。興味があればご覧ください。
参考文献
H.P.スウ(著) 佐藤平八(訳) フーリエ解析 工学基礎演習シリーズ1 第8章 P255-257