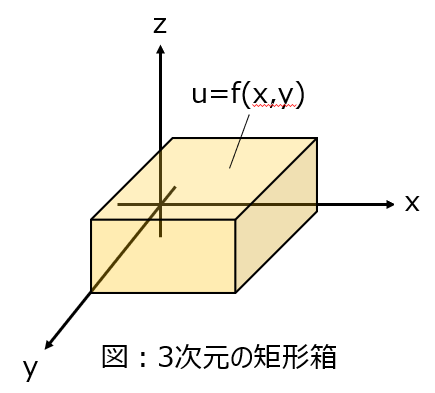
下記のように、\(x=a,y=b,z=c\)の3次元の矩形型の箱を考える。\(z=c\)の境界面でのポテンシャルを\(f(x,y)\)、\(z=c\)を除くすべての境界面において、ポテンシャル\(u(x,y,z)=0\)のとき、箱内部のポテンシャル分布をラプラス方程式を用いて求めよ。なお、ラプラス方程式は下記で与えられる。
\begin{aligned}\Delta u(x,y,z)=0\end{aligned}
はじめに
以前の記事で、一次元の偏微分方程式、二次元の偏微分方程式に対し、フーリエ変換、級数を用いた解法を説明してきました。
本記事では、三次元の偏微分方程式に対する級数解法をラプラス方程式を用いて説明していきます。
解答例
一変数、二変数の場合と同じく、変数が増えた分だけ変数分離をします。分離する数が増えた分、連立式は増えますが、一つ一つ丁寧に解いていきます。
\(u(x,y,z)=X(x)Y(y)Z(z)\)と変数分離をし、(1)式に代入すると
\begin{aligned}X^{\prime \prime}(x)Y(y)Z(z)+X(x)Y^{\prime \prime}(y)Z(z)+X(x)Y(y)Z^{\prime \prime}(z)=0\end{aligned}
両辺\(X(x)Y(y)Z(z)\)で割ると
\begin{aligned}-\dfrac{X^{\prime \prime}(x)}{X(x)}=\dfrac{Y^{\prime \prime}(y)}{Y(y)}+\dfrac{Z^{\prime \prime}(z)}{Z(z)}=k^{2}_{x}\end{aligned}
と、定数\(k^{2}_{x}\)で表すことができる。これを用いて
\begin{aligned}X^{\prime \prime}(x)+k_{x}^{2}X(x)=0\end{aligned}
になる。\(Y(y),Z(z)\)に関しても同様にして
\begin{aligned}-\dfrac{Y^{\prime \prime}(y)}{Y(y)}=\dfrac{Z^{\prime \prime}(z)}{Z(z)}-k^{2}_{x}=k^{2}_{y}\end{aligned}
と表せるので
\begin{cases}Y^{\prime \prime}(y)+k_{y}^{2}Y(y)=0 \\ Z^{\prime \prime}(z)-k_{z}^{2}Z(z)=0\end{cases}
とおける。ただし、\(k^{2}_{z}=k^{2}_{x}+k^{2}_{y}\)である。
(4)式、(6)式により、それぞれの変数の一般解は
\begin{cases}X(x)=A\cos k_{x}x+B \sin k_{x}x \\ Y(y)=C\cos k_{y}y+D \sin k_{y}y \\ Z(z)=E \cosh k_{z}z +F \sinh k_{z}z \end{cases}
問題文より、下記の境界面でポテンシャル0となる。
\begin{cases}X(0)=X(a)=0 \\ Y(0)=Y(b)=0 \\ Z(0)=0\end{cases}
これを(7)式に代入することで
\begin{cases}X(0)=A=0 \\ X(a)=B \sin k_{x}a=0 \\ Y(0)=C=0 \\ Y(b)=D \sin k_{y}b=0 \\ Z(0)=E=0\end{cases}
以上より、\(k_{x}=\dfrac{m \pi }{a},k_{y}=\dfrac{ n \pi}{b}=0\)
\begin{aligned}k_{z}=\pi \sqrt{\dfrac{m^{2}}{a^{2}}+\dfrac{n^{2}}{b^{2}}}\end{aligned}
\begin{cases}X_{m}(x)=B_{m}\sin \dfrac{m \pi x}{a} \\ Y_{n}(y)=D_{n}\sin \dfrac{n \pi x}{b} \\ Z_{mn}(z)=F_{mn} \sinh k_{z}z\end{cases}
これを\(u(x,y,z)=X(x)Y(y)Z(z)\)に代入すると
\begin{aligned}u_{mn}(x,y,z)=B_{m}D_{n}F_{mn}\sin \dfrac{m \pi x}{a}\sin \dfrac{n \pi x}{b}\sinh k_{z}z\end{aligned}
以上が、ポテンシャル0になる部分の境界条件を満たす解になる。\(z=c\)分の境界条件\(u(x,y,c)=f(x,y)\)も考える。
\begin{aligned}f(x,y)=\sum^{\infty}_{m=1}\sum^{\infty}_{n=1}B_{m}D_{n}F_{mn}\sin \dfrac{m \pi x}{a}\sin \dfrac{n \pi x}{b}\sinh k_{z}z\end{aligned}
を仮定すると、フーリエ級数展開により
\begin{aligned}B_{m}D_{n}F_{mn}\sinh k_{z}c=\dfrac{4}{ab}\int^{b}_{0}\int^{a}_{0}f(x,y) \sin \dfrac{n \pi x}{a} \sin {n \pi y}{b} dx dy\end{aligned}
最後に
偏微分方程式を級数展開で解く行為は、仮定の元に成り立っています。知識で助けられることが多いため、是非、解く順序を覚えることを推奨します。