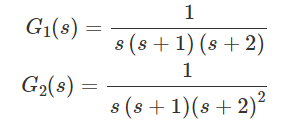【問題】下記の閉ループ伝達関数\(H_{1}(s),H_{2}(s)\)に単位ステップ関数\(X(s)=\frac{1}{s}\)を入力したとき、以下の出力\(G_{1}(s),G_{2}(s)\)を得る。それぞれの結果を逆ラプラス変換し、定常偏差を求めよ。
\begin{eqnarray}H_{1}(s) =\dfrac{1}{\left( s+1\right) \left( s+2\right) } \\ H_{2}(s) =\dfrac{1}{\left( s+1\right) \left( s+2\right)^{2} } \\ G_{1}(s) =\dfrac{1}{s\left( s+1\right) \left( s+2\right) } \\ G_{2}(s) =\dfrac{1}{s\left( s+1\right) \left( s+2\right)^{2} }\end{eqnarray}
はじめに
本問の知識は、制御工学でよく使います。
システムをラプラス変換し、その結果を逆ラプラス変換。システム全体の出力を時間(t)軸で求める。というパターン問題が頻出です。
この過程で、手計算では逆ラプラス変換できない複雑な伝達関数が良く出てきます。
部分分数分解によって変換できる形に式変形する。が常套手段ですが、計算ミスが多く発生します。加えて、限られた試験時間の中で単純な式変形に時間を費やしてしまいます。
本問では、ヘビサイドの展開定理を用い、複雑な伝達関数の部分分数分解を迅速に行う方法を紹介します。
部分分数分解を用いた解法
まずは、一般的な解法から説明します。
高校数学で勉強したように、下記のように部分分数分解できます。
\begin{eqnarray}\dfrac{1}{s\left( s+1\right) \left( s+2\right) }=\dfrac{A}{5}+\dfrac{B}{s+1}+\dfrac{C}{s+2} \\ 1=A\left( s+1\right) \left( s+2\right) +Bs\left( s+2\right) +Cs\left( s+1\right) \\ =\left( A+B+C\right) s^{2}+\left( 3A+2B+C\right) s+2A\end{eqnarray}
\begin{cases}A+B+C=0\\ 3A+2B+C=0\\ 2A=1\end{cases}
より、\(A=\dfrac{1}{2},B=-1,C=\dfrac{1}{2}\)
結構計算に時間がかかりました。。。
続いて、\(G_{2}(s)\)分です。2次が分母の項は、1次の場合と項を分けないといけないので
\begin{flalign}\dfrac{1}{s\left( s+1\right) \left( s+2\right) ^{2}}=\dfrac{A}{s}+\dfrac{B}{s+1}+\dfrac{C}{\left( s+2\right) ^{2}} +\dfrac{D}{s+2} \\ 1=A\left( s+1\right) \left( s+2\right) ^{2}+Bs\left( s+2\right) ^{2} +Cs\left( s+1\right) +Ds\left( s+1\right) \left( s+2\right) \\ =A\left( s+1\right) \left( s^{2}+4s+4\right) +Bs\left( s^{2}+4s+4\right) +Cs^{2}+Cs+Ds\left( s^{2}+3s+2\right) \\ =\left( A+B+D\right) s^{3}+\left( 5A+4B+C+3D\right) s^{2} +\left( 4B+8A+C+2D\right) +4A \end{flalign}
\(s^{0}\)項に注目すると、\(A=\dfrac{1}{4}\)
\begin{cases}B+D=-\dfrac{1}{4}\\ 4B+C+3D=-\dfrac{5}{4}\\ 4B+C+2D=-2\end{cases}
2式と3式に注目し、\(D=\dfrac{3}{4}\)
\(C=-2+4-2*\dfrac{3}{4}=\dfrac{1}{2}\)
よって、\(G_{2}(s)=\dfrac{1}{4s}-\dfrac{1}{s+1}+\dfrac{1}{2\left( s+1\right) ^{2}}+\dfrac{3}{4\left( s+1\right) }\)
なかなか計算に時間がかかりました。。。試験だと3,4分は損しそうです。
結構馬鹿にならない時間だと思います。単純に式を変更するだけに使いたくないはずです。
そこで、下記に紹介するヘビサイドの公式を使用すれば、部分分数分解がすぐに完了することを示します。
ヘビサイドの展開公式
公式はググると出てきますが、基本は下記のように覚えるとOKです。
求める係数に紐づく分母を消去した伝達関数に対し、消去した分母の極を代入する。
実際に計算すると理解が進みます。
(i)\(G_{1}(s)\dfrac{1}{s\left( s+1\right) \left( 5+2\right) }=\dfrac{A}{5}+\dfrac{B}{s+1}+\dfrac{C}{s+2}\)について、ヘビサイドの展開公式より
\(A= \dfrac{1}{\left( s+1\right) \left( s+2\right) }| _{s=0}=\dfrac{1}{2}\)
\(B= \dfrac{1}{s\left( s+2\right) }| _{s=-1}=-1\)
\(C = \dfrac{1}{s\left( s+1\right) }| _{s=-2}=\dfrac{1}{2}\)
と、代入する分母の極抜きの伝達関数を使用して計算するとすぐに値が出ました。
(ii)\(G_{2}(s)=\dfrac{1}{s\left( s+1\right) \left( s+2\right)^{2} }\)について、同様にして
\(A= \dfrac{1}{\left( s+1\right) \left( s+2\right) ^{2}}| _{s=0}=\dfrac{1}{4}\)
\(B= \dfrac{1}{s\left( s+2\right) ^{2}}| _{s=-1}=-1\)
\(C= \dfrac{1}{s\left( s+1\right) }| _{s=-2}=\dfrac{1}{2}\)
\(D=\dfrac{d}{ds}\left( \left( s+2\right) ^{2}\dfrac{1}{s\left( s+1\right) \left( s+2\right) ^{2}}\right) |_{ s=-2}\\ =-\dfrac{2s+1}{s^{2}\left( s+1\right) ^{2}}=\dfrac{3}{4}\)
です。すぐに値が出てきました。
※注意点として、分母が2次の項の係数を求める際は、微分が必要です。結局、複素関数で留数を求めるときと同じ計算をすればOKです。
求めた値が不安ならば、検算しても良いと思います。その時間を差し引いても素直に部分分数分解するよりも早く結果が求まります。
結局、\(G_{1}(s),G_{2}(s)\)の逆ラプラス変換は以下のようになります。
\(G_{1}\left( s\right) =\dfrac{1}{25}-\dfrac{1}{s+1}+\dfrac{1}{2\left( s+2\right) }\)より
\(g_{1}(t)\left( t\right) =\dfrac{1}{2}-e^{-t}+\dfrac{1}{2}e^{-t}\)
\(G_{2}(s)=\dfrac{1}{4s}-\dfrac{1}{s+1}+\dfrac{1}{2\left( s+1\right) ^{2}}+\dfrac{3}{4\left( s+1\right) }\)より
\(g_{2}(t)=\dfrac{1}{4}-e^{-t}+\dfrac{1}{2}te^{-2t}+\dfrac{3}{4}e^{-2t}\)
結果
結局、t→∞を考えたとき
\(g_{1}(∞)=1/2\quad,g_{2}(∞)=1/4\)になります。
それぞれ、単位ステップ入力1に対し、1/2、3/4の偏差となります。
最終値の定理を使うと、偏差はすぐに求まりますが、大学によっては逆ラプラス変換からt→∞の極限を考えて偏差を求めるよう誘導する場合もあります。
是非、2パターンの方法で偏差を求められるよう勉強しておきたいです。
補足
本問では、伝達関数\(H_{1}(s),H_{2}(s)\)に単位ステップ関数を入力した前提でお話をしていました。
見方によっては、伝達関数\(G_{1}(s),G_{2}(s)\)に単位インパルス関数を入力したときの出力としても捉えることができます。
発散しないためシステムは安定ですが、ほんの少しの入力に対しても偏差が発生するようなシステムだ。というイメージを持つと良いかもしれません。
最後に
本問は、制御工学で必要な計算方法、結果の考察方法の基本について紹介しました。
次回以降、システムブロックを元に安定性などを議論する記事記載していく予定です。
こちらの記事で計算の基本と工夫する方法を押さえておきましょう。