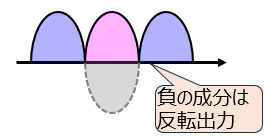
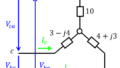
正弦波電圧を全波整流回路に入力する状況を考える。以下の問いに答えよ。
(1)正弦波電圧\(v_{i}=|V_{o}\sin2 \pi f t|\)をフーリエ級数展開して示せ。なお、第二高調波成分までで良い。
(2)上記の電圧が抵抗\(R\)に接続されているとき、抵抗で消費される電力を求めよ。また、直流成分で消費される電力は全体の何%に当たるか答えよ。
整流回路とは
電流を一方の方向に出力する回路を言います。代表的な回路に、半波整流回路、全波整流回路があります。
半波整流回路
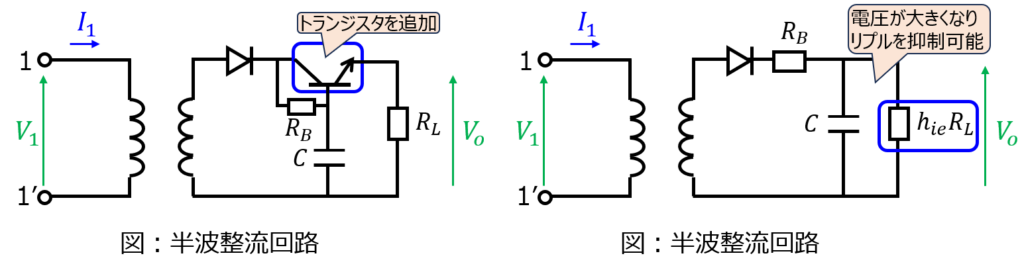
下記に代表的な構成を示します。一次側の入力に対し、二次側にダイオードを置きます。ダイオードには逆方向の電流は流れないため、出力電圧は入力電圧の半サイクル分の出力になります。
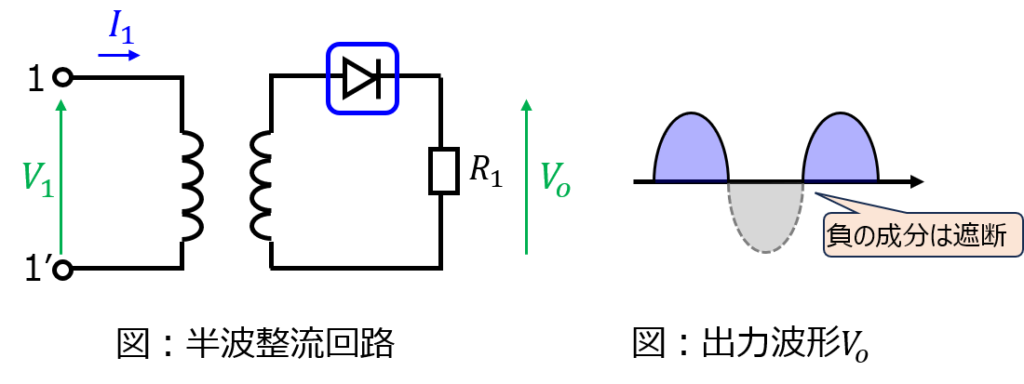
出力波形のうち、直流分以外の成分をリプルと呼んでいます。直流の出力が必要な場面ではノイズとなりますので、平滑コンデンサを置き、交流成分を阻止する構成もあります。
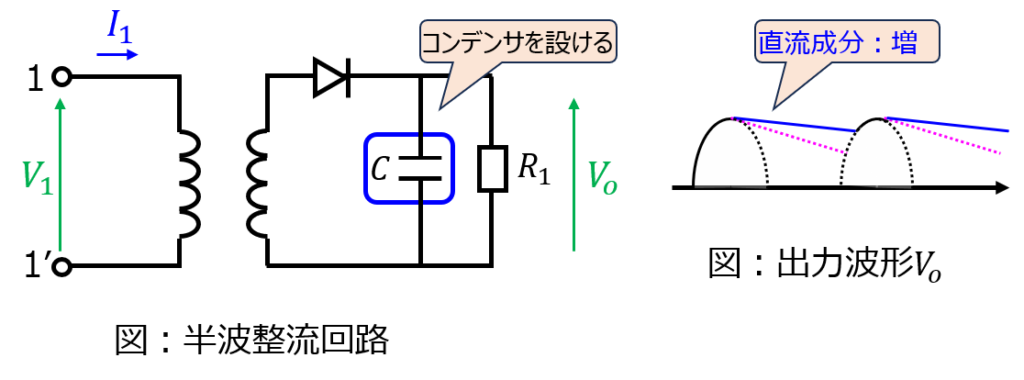
他、トランジスタも追加してリプルを抑える構成もあります。これは、小信号等価回路で表した時の\(h_{ie}\)が抵抗を2桁倍するため、並列に接続しているコンデンサにとっても電圧が2桁倍になります。よって、コンデンサの容量が大きくなったとみることができ、さらにリプルを抑制できます。
全波整流回路
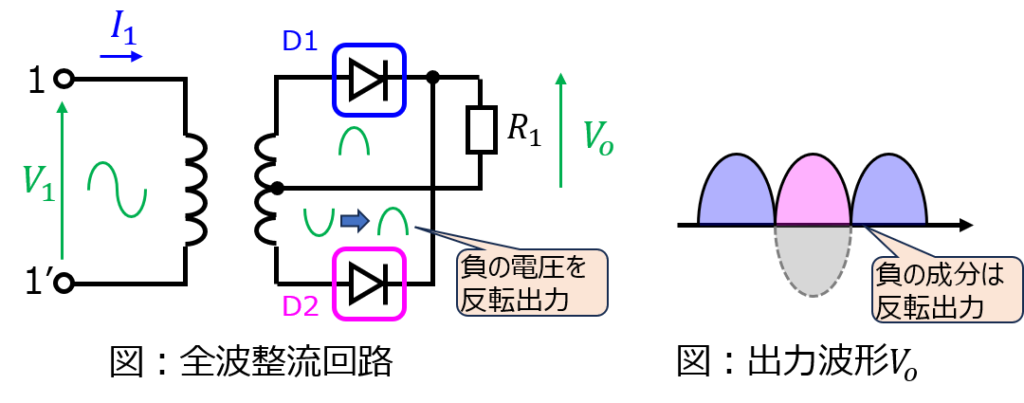
下記に代表的な構成を示します。半波整流の場合はダイオードが一つだけだったのが、全波整流では2つ接続します。また、変圧器には中間タップが接続されており、極性の違いから、下側のダイオード\(D_{2}\)を流れる電流は反転します。これより、負の半サイクルも正に出力でき、入力電圧の全てを整流することができます。
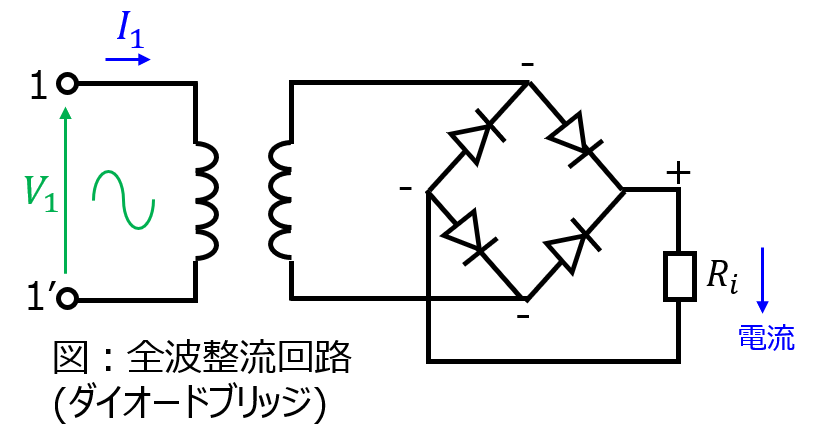
また、ダイオードブリッジを使用する構成もあります。同じく、入力電圧が正の半周期では左斜め上とその対角線上のダイオードを通り、負の半周期ではもう一対のダイオードを流れます。


高調波成分とは
任意の信号は、フーリエ級数展開すると離散的な周波数を持つ信号の重ね合わせで表現できます。すると、基準の周波数の3倍、5倍・・と高周波の成分も存在することになります。
これを高調波を言い、ノイズの原因となります。
本問で与えた信号\(v_{i}=|V_{o}\sin2 \pi f t|\)も、式だけ見るとsin波が正の領域で存在しているだけです。しかし、負の電圧を正に折り返す反転部分で急峻な信号変化が出ています。この部分で、どうしても高調波は発生しています。
対策としては、ローパスフィルタを置くことです。コンデンサで高周波分の信号をGNDに落とすことで高周波を除去できます。(ただし、あまりにも低次の波まで遮断すると信号自体の復元ができなくなります。ですので、ある程度閾値に余裕は持たせておく必要はあります。ローパスフィルタの詳しい原理は、こちらの記事で紹介しています。)
本問では、全波整流した波形にどの程度の高調波が含まれているのかを確認していきます。
解答例
(1)全波整流波形のフーリエ級数展開
与えられた波形はf(t)=f(-t)より偶関数である。よって、フーリエ級数展開において、\(a_{n}=0\)である。\(b_{n}\)だけ考えれば良い。
第二高調波まで考えれば良いので、n=0,1,2の3通り考えていく。
n=0のとき
\begin{aligned}b_{0}&=f\int^{1/2f}_{-1/2f} |V_{o}\sin 2 \pi f t|dt \\ &=2V_{o}f \int^{1/2f}_{0} \sin 2 \pi f t dt \\ &=2V_{o}f\dfrac{1}{2\pi f}2 \\ &=\dfrac{ 2V_{o}}{f}\end{aligned}
n=1のとき
\begin{aligned}b_{1}&=2f\int^{1/2f}_{-1/2f} |V_{o}\sin 2 \pi f t| \cos (2 \pi ft) dt \end{aligned}
であるが、同じ周波数のsinθ、cosθの積は倍角の公式を用いると1/2sin2θとなる。θが2倍になるので、半周期分の積分でも結果は0になる。
以上から、\(b_{1}=0\)
n=2のとき
\begin{aligned}b_{2}&=2f\int^{1/2f}_{-1/2f} |V_{o}\sin 2 \pi f t| \cos (4 \pi ft) dt \\ &=2V_{o}f\left(\int^{0}_{-1/2f}-\sin 2 \pi f t \cos 4\pi ft dt + \int^{1/2f}_{0}\sin 2 \pi f t \cos 4\pi ft dtdt \right)\end{aligned}
積和の公式を用いると
\begin{aligned}b_{2}&=V_{o}f\left(\int^{0}_{-1/2f}-\sin6\pi ft dt-\int^{0}_{-1/2f}-\sin6\pi ft dt -\int^{1/2f}_{0}-\sin2\pi ft dt-\int^{1/2f}_{0}\sin6\pi ft dt \right) \\ &=\dfrac{V_{o}}{\pi}\left(\left \lbrack 2\dfrac{1}{6}\cos 6 \pi f t \right \rbrack^{0}_{-1/2f} +\left \lbrack 2\dfrac{1}{6}\cos 2 \pi f t \right \rbrack^{0}_{-1/2f} \right) \\ &=-\dfrac{4V_{o}}{3 \pi} \end{aligned}
(2)直流成分の消費電力の割合
全体の消費電力を\(P_{o}\)、直流成分の消費電力を\(P_{1}\)とする。
まず、全体の消費電力は、電圧の実効値が\(\frac{V_{o}}{\sqrt{2}}\)なので
\begin{aligned}P_{o}=\dfrac{V^{2}}{R}=\dfrac{V_{o}^{2}}{2R}\end{aligned}
次に、直流分の消費電力\(P_{1}\)は、\(b_{0}\)の結果を用いて
\begin{aligned}P_{o}=\dfrac{V^{2}}{R}=\dfrac{4V_{o}}{\pi^{2}R}\end{aligned}
これの比を取ると、下記の計算より81%であることが分かる。
\begin{aligned}\dfrac{P_{1}}{P_{o}}=\dfrac{8}{\pi^{2}}=0.81\end{aligned}
最後に
高調波に関する知識は、電験(法規)でよく出てきます。将来電気関係の仕事に就く方は覚えておきましょう。