(1)ある回路に流れる電流、電圧がそれぞれ下記の式で表される。複素電力、皮相電力、有効電力、無効電力、力率を求めよ。
\begin{cases}v(t)=100\sqrt{2}\sin(120\pi t +\frac{5}{18}\pi) \\ i(t)=5\sqrt{2}\sin(120 \pi t -\frac{1}{9}\pi)\end{cases}
(2)図(a)の電気回路における皮相電力、力率、有効電力、無効電力を求めよ。
(3)図(b)の電気回路において、インピーダンス\(Z=r+jX\)で消費される有効電力と無効電力を求めよ。

有効電力とは
電流ベクトルと電圧ベクトルの内積を言います。(実効電力とも言います。)
有効電力を\(P\)とすると、下記のように表されます。
\begin{aligned}P=\boldsymbol{V}\boldsymbol{I}=VI\cos \theta\end{aligned}
となり、どちらかのベクトルの正射影をもう一方のベクトルと掛け合わせることで求められます。
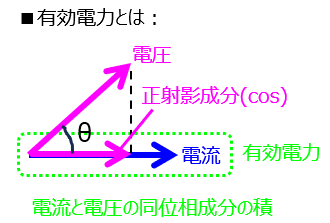
\(\cos \theta\)は力率と呼び、1に近づくほど回路に流れている電流が使用されていると判断できます。
電圧も電流も同位相の成分を掛け合わせていることから、電気エネルギーとなります。単位は[W]であり、家庭用電気機器を初め、あらゆる機器で消費されています。
無効電力とは
電流ベクトルと電圧ベクトルの直交成分の積を言います。
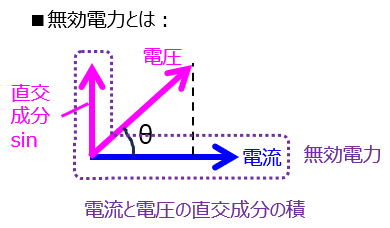
有効電力の場合、(1)式により\(\cos\)項でしたが、無効電力の場合は\(\sin\)項を使用し
\begin{aligned}Q=\boldsymbol{V}\boldsymbol{I}=VI\sin \theta\end{aligned}
で表されます。電流と電圧の直交成分を考えているため、電気機器の仕事には利用できません。(Iがsinθ、Vがcosθで表される場合、VIはsin2θに合成できます。これを1周期[0,2π]分積分すると0になることから、仕事をしていない。と分かります。)
また、電圧一定の立場において、無効電力が大きくなると回路に流れる電流が大きくなり、配線抵抗によるジュール損失が大きくなります。
無効電力の利用方法
前段の説明では、無効電力は不要かのようにお話ししましたが、実際そんなことはありません。確かに、過度に持ってしまうと悪影響が出ますが、下記の場面で役立ちます。
系統の電圧安定化に用いる。
- 逆潮流防止のため、無効電力を消費し、電圧を下げる。
- 誘導電動機など、誘導性負荷を接続したときの位相調整のため、予め進み無効電力を確保しておく。
1.に関して、逆潮流は、太陽光発電を始めとする再生可能エネルギーにより発生します。
通常、電力会社から一般家庭に対して電力を送電しますが、逆のことが発生する事象を言います。
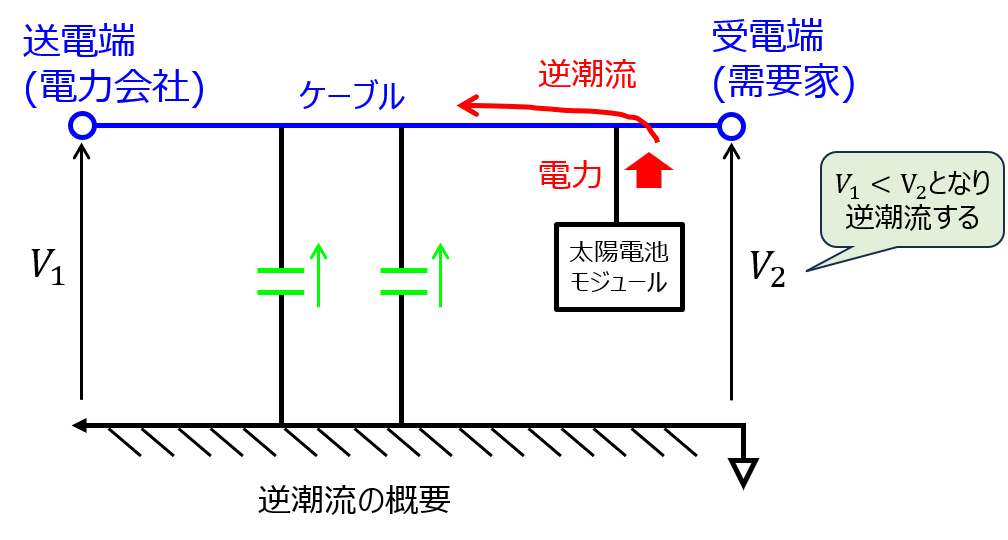
これは、太陽光発電は一般家庭側で実施することが多いため発生します。需要家側の電圧が上がる。➡逆潮流が発生する。という理由です。
ですが、無効電力を持っていれば、その分を消費することで電圧調整が可能です。これにより、逆潮流を防止できます。
2.に関して、系統に接続する負荷の特性次第で、逆向きの位相を持った無効電力を予め持っておく運用ができます。
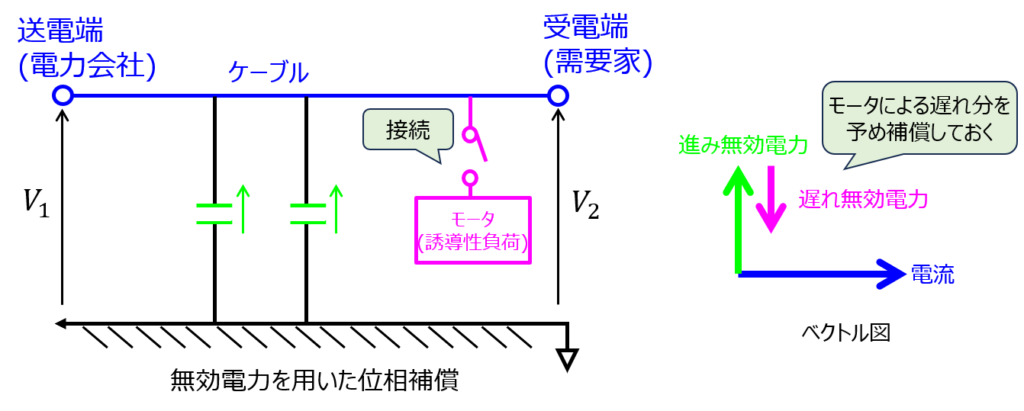
これにより、実際に負荷を接続したとき、無効電力が発生せず、消費側に働くことができます。(力率改善)
進み無効電力を発生させたいときは、進相コンデンサ。
遅れ無効電力を発生させたいときは、分路リアクトルを系統に接続します。(電験で出ます。)
皮相電力とは
無効電力と有効電力のベクトルを合成した見かけ上の電力になります。皮相電力を\(P_{a}\)とすると
\begin{aligned}P_{a}=\sqrt{P^{2}+Q^{2}}\end{aligned}
で表されます。単位は[V・A]で、回路を流れる電圧と電流をそのまま掛け算した。と言う単位系になっています。
よく、変圧器の容量の表記で出てきます。これは、実際に電力で消費する機器ではなく、エネルギーを変換する機器であることから、無効電力分も含めて考える必要があるからです。
なお、皮相電力を用いて、力率\(\cos\theta\)は
\begin{aligned}\cos \theta=\dfrac{P}{P_{a}}\end{aligned}
で表されます。問題を解くうえで、こちらの式を用いて求めることが多いです。是非覚えておきましょう。
複素電力とは
電圧ベクトル\(\boldsymbol{V}\)と電流ベクトルの共役複素数\(\boldsymbol{\widehat{I}}\)の積を言います。
\begin{aligned}S=\boldsymbol{V}・\boldsymbol{\widehat{I}}\end{aligned}
で表されます。
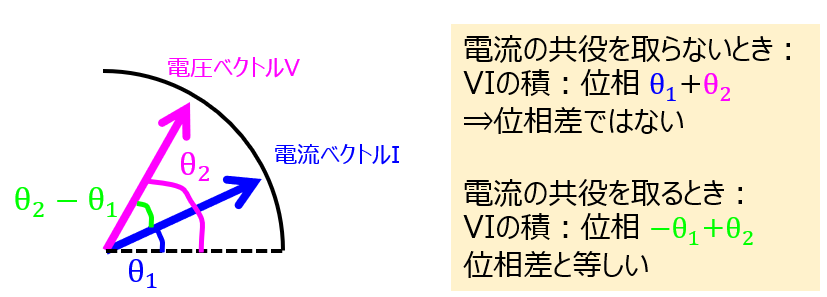
共役複素数とし、電流の位相を\(e^{i\beta}\)から\(e^{-i\beta}\)に反転させるには理由があります。電流ベクトルと電圧ベクトルの位相差を表現できるからです。
有効電力の章で説明したように、電流ベクトルと電圧ベクトルの内積が実効電力となります。内積は、二つのベクトルの位相差\(\cos\theta\)で考えます。
反転無しの場合、電圧の位相\(e^{i\alpha}\)と足し合わせとなってしまい、位相差を正しく表現できません。
ここで、電流ベクトルを共役にしてやれば、電圧の位相に対して引き算ができ、差分が位相差になるわけですね。
計算をすると、\(a+jb\)項のように実部と虚部が発生します。実部が有効電力に対応し、虚部が無効電力に対応します。
理由は、exp項がオイラーの公式により、\(\cos \theta+j \sin \theta\)になるためです。(1)式、(2)式はそれぞれ有効電力、無効電力で、cos項、sin項を持っているため、上記の解釈が出来ます。
解答例
(1)
与えられた電圧、電流をフェーザ表示すると
\begin{cases}V=100e^{j \frac{5}{18}\pi} \\ I=5e^{j\frac{1}{9}\pi} \end{cases}
複素電力
\begin{aligned}S&=V\overline{I} \\ &=100e^{j\frac{1}{6}\pi} \\ &=250\sqrt{3}+j250\end{aligned}
これより、有効電力は250[W]、無効電力は250[Var]
皮相電力は、\(\sqrt{250^{2}+250{2}}=250 \sqrt{2}[VA]\)
有効電力と無効電力が等しいので、力率はcos(45°)=1/√2
(2)
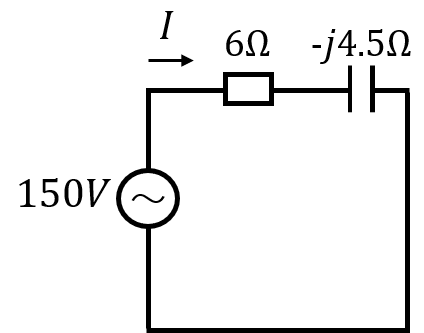
回路のインピーダンス\(Z\)は
\begin{aligned}Z=6-j4.5\end{aligned}
よって、回路に流れる電流\(I\)は
\begin{aligned}I&=\dfrac{150}{6-j4.5} \\ &=16+j12\end{aligned}
よって、求める複素電力は
\begin{aligned}S&=V\overline{I} \\ &=150(16j-12)\end{aligned}
よって、求める皮相電力、有効電力、無効電力は
\begin{cases}P_{a}=150\sqrt{16^{2}+12^{2}}=3000[VA] \\ P=150*16=2400[W] \\ Q=1800[Var]\end{cases}
(3)

回路に流れる電流\(I\)は
\begin{aligned}I=\dfrac{E}{R+r+j(\omega L+X)}\end{aligned}
以上より、インピーダンスZで消費する有効電力\(P\)と無効電力\(Q\)は
\begin{cases}P=r|I|^{2}=\dfrac{rE^{2}}{(R+r)^{2}+(\omega L+X)^{2}} \\ Q=X|I|^{2}=\dfrac{XE^{2}}{(R+r)^{2}+(\omega L+X)^{2}}\end{cases}


