(1)図1のような、RLとRCを並列に接続した回路の共振周波数を求めよ。
(2)図2のような、LC直列回路を並列接続したときの直列共振点、並列共振点を求めよ。
共振周波数とは
インピーダンスの虚部が0になる周波数を言います。このとき、抵抗成分のみ存在するため、力率が1(最大)の状態です。院試を初め、様々な試験で頻出問題になっています。
虚部が0になることから、回路にはインダクタ成分(遅れ)(jωL)、コンデンサ成分(1/jωC)なる素子が最低一つは付きます。周波数が大きくなると、インダクタ成分は大きくなり、コンデンサ成分は小さくなることから、両者の良い塩梅が共振周波数と言うことですね。
この特性を生かし、多くの周波数成分を持つ信号の中から特定の周波数成分を取り出したり、除去したりする周波数選択回路として使用することがあります。(詳しくは、Q値の記事で解説しています。)
直列共振の特性
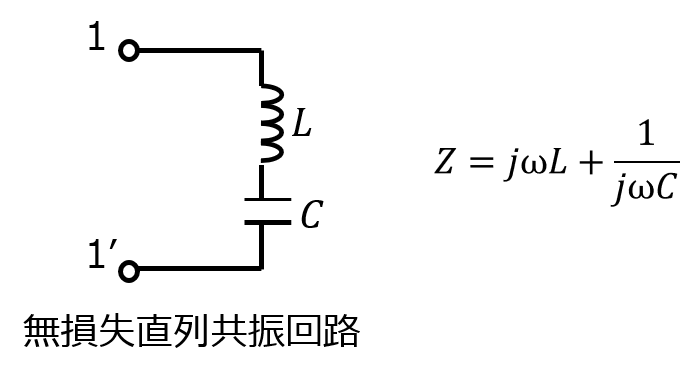
上記のような無損失直列共振回路(LC直列)を考えます。インピーダンス\(Z_{1}\)は
\begin{aligned}Z_{1}=j \omega L+\dfrac{1}{j \omega C}\end{aligned}
で、虚部=0を与える周波数は、\(\omega_{o}=\dfrac{1}{2 \pi \sqrt{LC}}, f_{o}=\dfrac{1}{2 \pi \sqrt{LC}}\)です。これを直列共振周波数と呼びます。
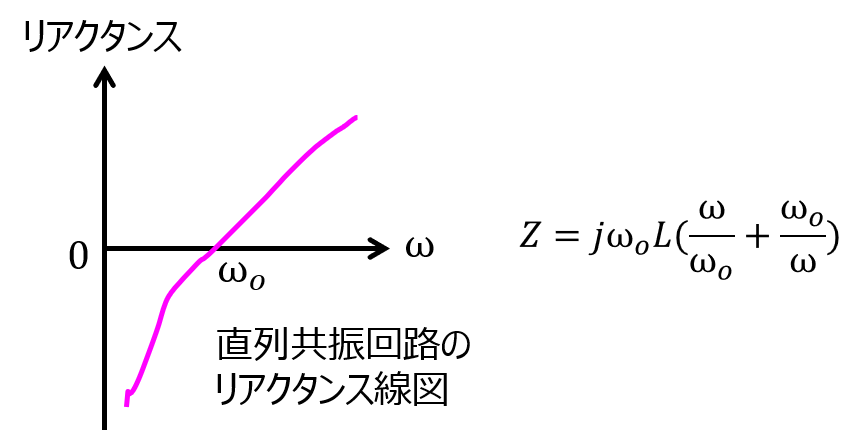
共振角周波数\(\omega_{o}\)の記号を用いて、(1)式を下記のように変形します。
\begin{aligned}Z=j \omega_{o}L\left(\dfrac{\omega}{\omega_{o}}-\dfrac{\omega_{o}}{\omega}\right)\end{aligned}
\(\omega\)を大きくすると第1項が大きくなり、第2項が小さくなるので、リアクタンスは単調増加になります。これを直列共振回路のリアクタンス線図と言います。
並列共振の特性
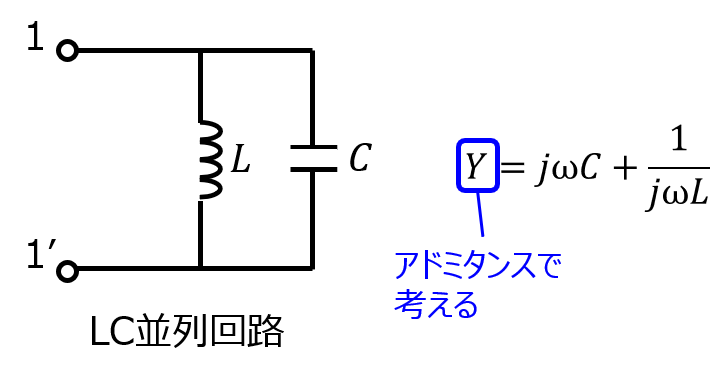
上記のようなLC並列回路を考えます。このとき、回路全体のアドミタンスは
\begin{aligned}Y=j \omega C +\dfrac{1}{j \omega C}\end{aligned}
共振周波数は、直列共振の場合と同じく\(\omega_{o}=\dfrac{1}{2 \pi \sqrt{LC}}, f_{o}=\dfrac{1}{2 \pi \sqrt{LC}}\)であるので
\begin{aligned}Y=j \omega C\left(\dfrac{\omega}{\omega_{o}}-\dfrac{\omega_{o}}{\omega}\right)\end{aligned}
並列共振回路の場合、インピーダンスの逆数、アドミタンスで考える必要がありますが、同様に単調増加であることが分かりました。
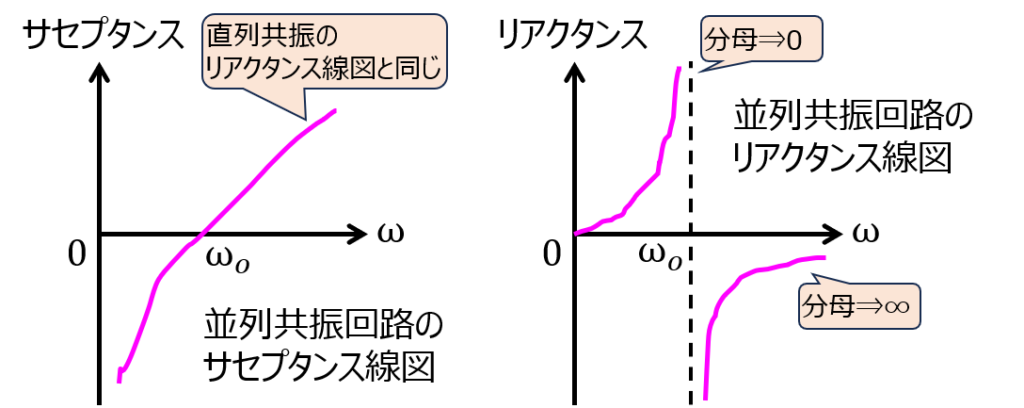
なお、インピーダンスとして考えると、上式の逆数を取れば良いのですから
\begin{aligned}Z=\dfrac{1}{j \omega C\left(\dfrac{\omega}{\omega_{o}}-\dfrac{\omega_{o}}{\omega}\right)}\end{aligned}
このとき、共振周波数では分母が0になるため、リアクタンスは発散します。よって、下記のようなリアクタンス線図になります。
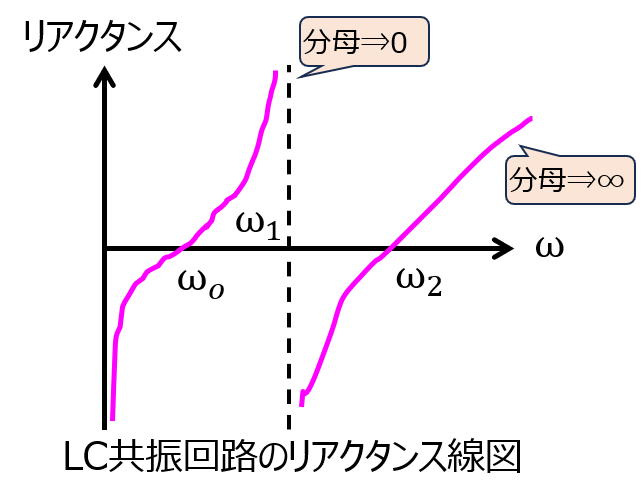
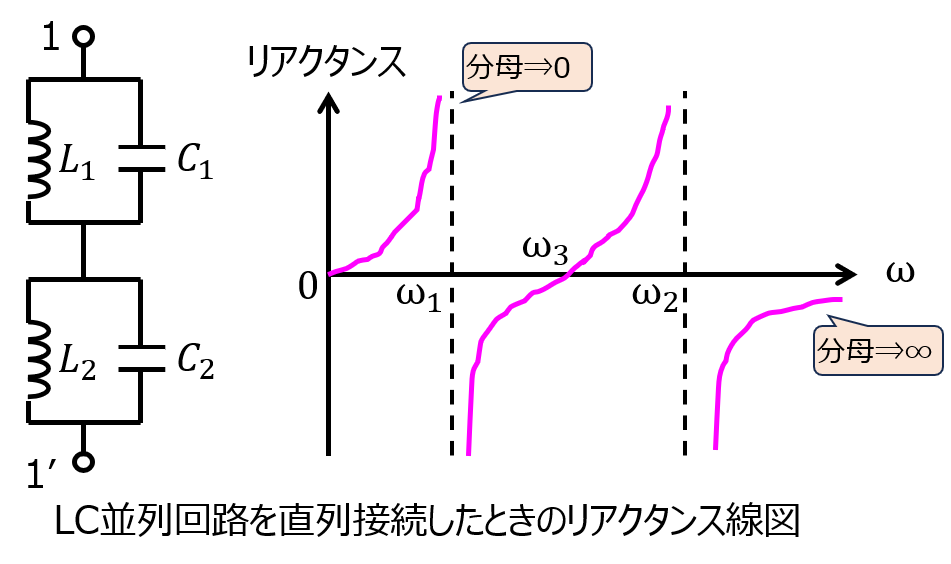
なお、共振周波数が異なるLC共振回路が存在するとき、リアクタンス線図はそれぞれの共振周波数で発散します。(下記に、\(L_{1}<L_{2},C_{1}<C_{2}\)の例を示します。)
\begin{aligned}Z=\dfrac{j \omega L_{1}}{1-\omega^{2}L_{1}C_{1}}+\dfrac{j \omega L_{2}}{1-\omega^{2}L_{2}C_{2}}\end{aligned}
で、分母=0を考えると、\(\omega_{1}=\dfrac{1}{\sqrt{L_{1}C_{1}}},\omega_{2}=\dfrac{1}{\sqrt{L_{2}C_{2}}}\)
このとき、リアクタンスは発散します。(逆に分子=0を与える\(\omega_{3}\)のとき、リアクタンスは0になります。)
直列共振、並列共振複合回路の共振特性
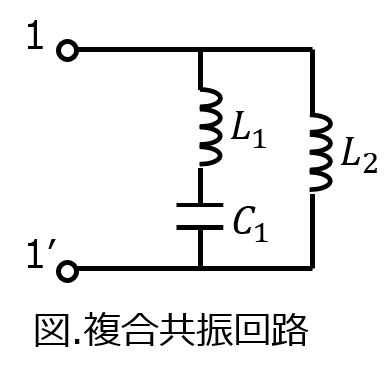
下記のように、並列回路の一方にLC、もう一方にLを配置する複合共振回路のリアクタンス線図を考えます。
リアクタンス線図としては、直列共振、並列共振ともに単調増加ですから、直列共振周波数および並列共振周波数さえ分かれば概形が書けそうです。
まず、回路全体のインピーダンスは
\begin{aligned}Z&=\dfrac{j \omega L_{2}\left( j \omega L+\dfrac{1}{j \omega C}\right)}{j \omega L_{2}+ j \omega L_{1}+\dfrac{1}{j \omega C}} \\ &=\dfrac{ j \omega L_{2}(1- \omega^{2}L_{1}C_{1})}{1- \omega^{2}C_{1}(L_{1}+L_{2})}\end{aligned}
直列共振の場合、インピーダンスが0になる周波数(分子=0)、並列共振の場合、インピーダンスが∞になる周波数(分母=0)を求めれば良いのですから、
\begin{cases}f_{1}=\dfrac{1}{2 \pi \sqrt{L_{1}C_{1}}} \\ f_{2}=\dfrac{1}{2 \pi \sqrt{(L_{1}+L_{2})C_{1}}}\end{cases}
第1式が直列共振周波数。第2式が並列共振周波数です。\(L_{1},L_{2}\)は正なので、\(f_{2}<f_{1}\)です。よって、リアクタンス線図は
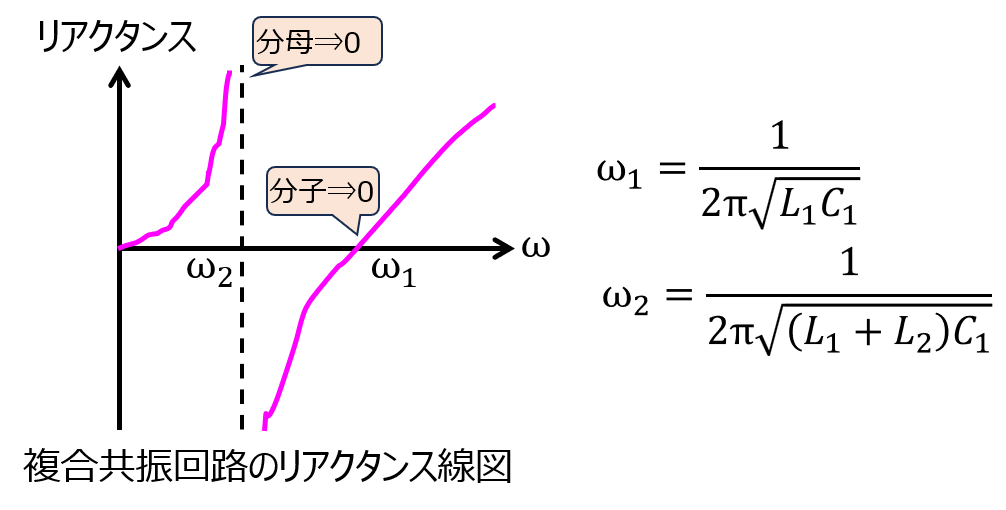
になります。
解答例
(1)共振周波数の計算
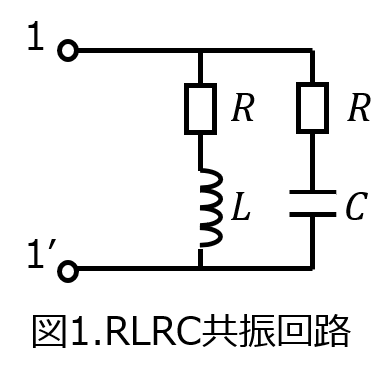
回路全体のアドミタンスは
\begin{aligned}Y&=\dfrac{1}{R+j \omega L}+\dfrac{1}{R+ \dfrac{1}{j \omega C}} \\ &=\dfrac{R-j \omega L}{R^{2}+(\omega L)^{2}}+\dfrac{\omega^{2} C^{2}R+j \omega C}{1+(\omega C R)^{2}}\end{aligned}
これの虚部が0になれば良いので
\begin{aligned}\dfrac{- \omega L}{R^{2}+(\omega L)^{2}}+\dfrac{j \omega C}{1+(\omega C R)^{2}}\end{aligned}
\begin{aligned}CR^{2}+ \omega^{2}L^{2}C=L+\omega^{2}LC^{2}R^{2}\end{aligned}
\begin{aligned}\omega^{2} L C(L-CR^{2})=L-CR^{2}\end{aligned}
\begin{aligned}\omega=\dfrac{1}{\sqrt{LC}}\end{aligned}
(2)直列、並列共振点の計算
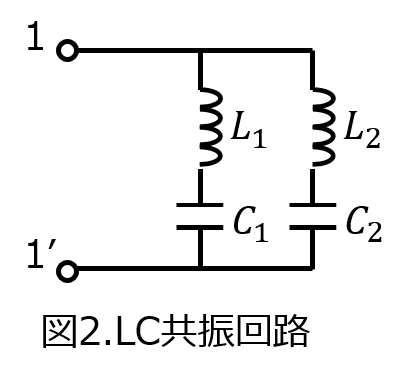
前節で行ったように、インピーダンス成分を求め、分子=0,分母=0を与える周波数を考えれば良いです。
\begin{aligned}Z=\dfrac{(\omega L_{1}-\dfrac{1}{\omega C_{1}})(\omega L_{2}-\dfrac{1}{\omega C_{1}})}{\omega L_{1}-\dfrac{1}{\omega C_{1}}+\omega L_{2}-\dfrac{1}{\omega C_{2}}}\end{aligned}
(分子)=0を与える周波数は
\begin{aligned}(1-\omega^{2} L_{1} C_{1})(1-\omega^{2} L_{2} C_{2})=0\end{aligned}
\begin{cases}\omega_{0}=\dfrac{1}{\sqrt{L_{1}C_{1}}} \\ \omega_{2}=\dfrac{1}{\sqrt{L_{2}C_{2}}}\end{cases}
続いて、(分母)=0を与える周波数は
\begin{aligned}1-\omega^{2} (L_{1}+L_{2})\dfrac{C_{1}C_{2}}{C_{1}+C_{2}}=0\end{aligned}
\begin{aligned}\omega_{1}=\dfrac{1}{\sqrt{(L_{1}+L_{2})\dfrac{C_{1}C_{2}}{C_{1}+C_{2}}}}\end{aligned}
\(\omega_{0}<\omega_{1}<\omega_{2}\)より、求めるリアクタンス線図は
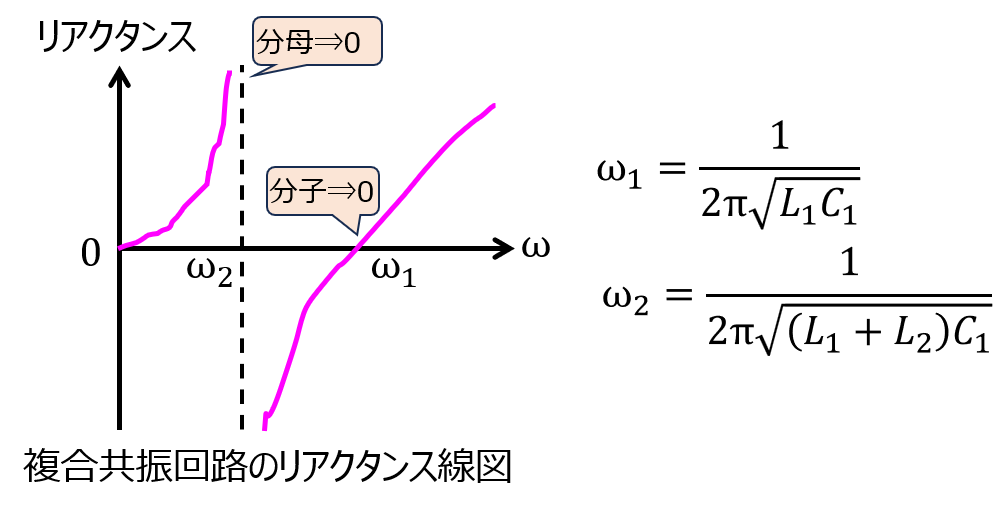
最後に
本問と似た問題が名大で出題されたことがあります。共振周波数を求めるだけでなく、リアクタンス線図の概形もイメージできるようにしましょう。