 情報
情報 【順序回路】Dフリップフロップを用いたシフトレジスタの設計
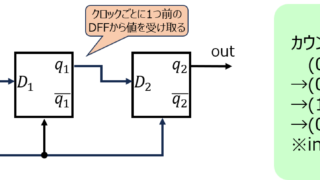
シフトレジスタとはクロックごとに、下位bitからその次の上位bitへ情報を伝搬する機能を持った回路を言います。下記の図に概要を示します。左のDFFに格納された値をクロックごとに右に伝搬していく構造となっています。
 情報
情報  情報
情報  情報
情報  情報
情報  情報
情報  情報
情報  情報
情報  情報
情報 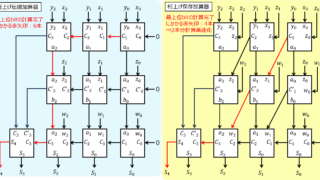 情報
情報  情報
情報