あるベクトル場
\begin{aligned}\boldsymbol{A}=(x+yz,y+x,z+3)\end{aligned}
に対し、\(S=((x,y,z)|4x^{2}+y^{2}+z=1,-3 \leqq z)\)で与えられた閉曲面を考える。下記の値を求めよ。
\begin{aligned}\int_{S}\boldsymbol{A} \cdot d\boldsymbol{S}\end{aligned}
ガウスの発散定理とは
ある閉曲面(3次元)内のベクトル場\(\boldsymbol{A}\)の発散\(div\boldsymbol{A}\)は、閉曲面を囲む閉曲面Sでベクトル場を面積分した値に等しいことを言います。
\begin{aligned}\int_{V} \Delta \boldsymbol{A} \cdot dV = \int_{S} \boldsymbol{A} \cdot d\boldsymbol{S}\end{aligned}
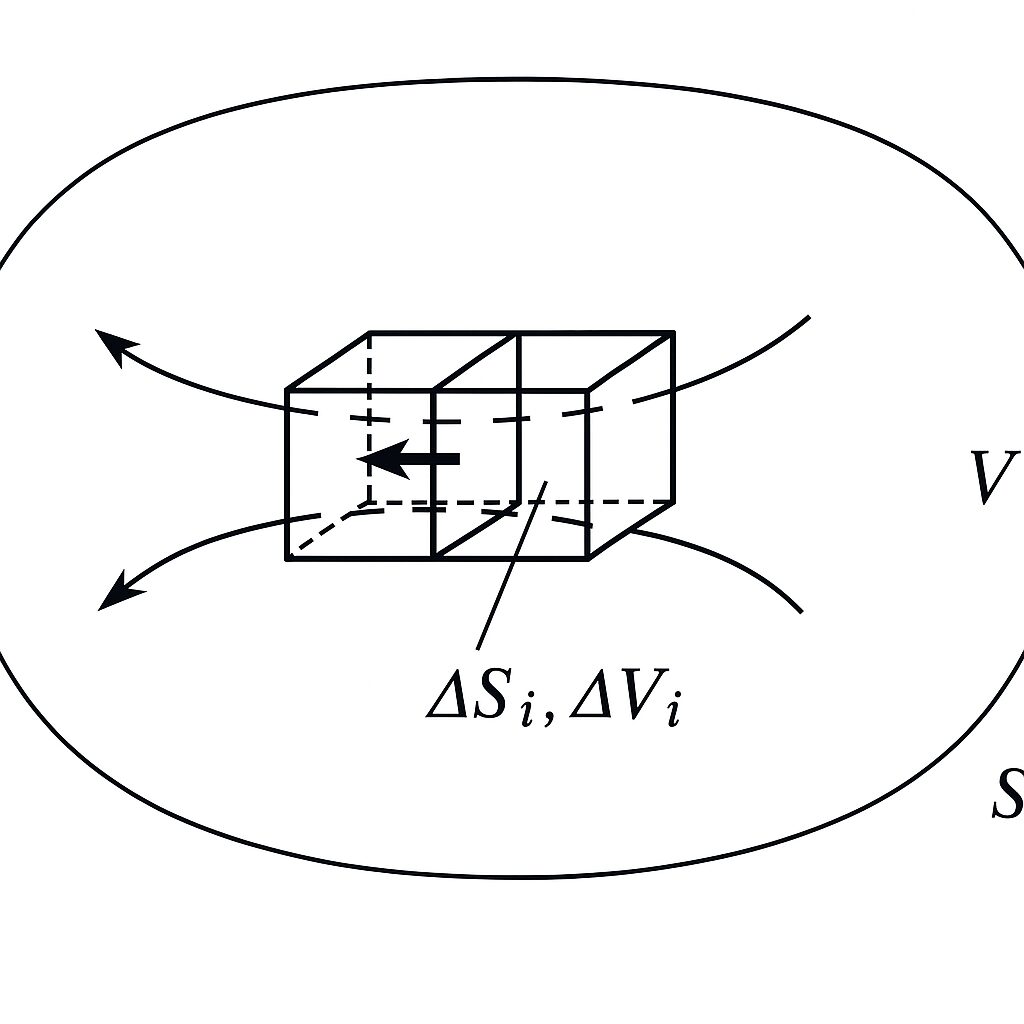
体積を囲む閉曲面内部の隣り合う2つの微小領域において、一方の領域から出たベクトルはそのまま隣の領域に入り出ていくわけですから、体積内部の面積分はお互いに打ち消し合います。よって、体積を囲む境界面だけ考えれば、内部の積分をわざわざ考えなくて良い。ということですね。
本問では、楕円放物線を例に計算していきます。
解答例
与えられた領域\(S=((x,y,z)|4x^{2}+y^{2}+z=1,-3 \leqq z) \)の体積\(V\)を考えます。
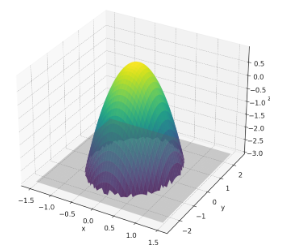
\(z\)の下限は-3、上限は\(1-4x^{2}-y^{2}\)であることが分かります。楕円放物面であり、下記のような概形になります。
\(x=r\cos\theta,y=2r\sin\theta\)で変数変換する。求めるヤコビアン\(J\)は
\begin{aligned}|J|&=\begin{vmatrix}\cos \theta & -r \sin \theta \\ 2\sin \theta & 2r \cos \theta\end{vmatrix} \\ &=2r\end{aligned}
\(0 \leqq r \leqq 1 , 0 \leqq \theta \leqq 2 \pi\)だから、求める体積\(V\)は
\begin{aligned}V&=\int\int_{(x,y)}dxdy\int^{1-4x^{2}-y^{2}}_{-3}dz \\ &=\int\int_{(x,y)}(4-4x^{2}-y^{2})dxdy\end{aligned}
\(4x^{2}+y^{2}=4r^{2}\)なので上式は
\begin{aligned}V&=\int^{2 \pi}_{0}d\theta \int^{1}_{0}(4-4r^{2}) \cdot 2r dr \\ &=2 \pi \cdot 2[2r^{2}-r^{4}]^{1}_{0} \\ &=4 \pi\end{aligned}
与えられたベクトル場\(\boldsymbol{A}=(x+yz,y+x,z+3)\)の発散は
\begin{aligned}div \mathrm{\boldsymbol{A}}=1+1+1=3\end{aligned}
与えられた閉曲面\(S\)を、底面\(S_{1}\)と放物面\(S_{2}\)に分割する。求める計算値は下記のように変形できる。
\begin{aligned}\int_{S} \boldsymbol{A}\cdot d\boldsymbol{S}=\int_{S_{1}}\boldsymbol{A} \cdot d\boldsymbol{S}+\int_{S_{2}}\boldsymbol{A} \cdot d\boldsymbol{S}\end{aligned}
ここで、底面\(S_{1}\)は\(z=-3\)であり、鉛直ベクトル\(\boldsymbol{n}=(0,0,1)\)だから、ベクトル\(\boldsymbol{A}\)との内積は
\begin{aligned}\boldsymbol{A} \cdot \boldsymbol{n}=0+0+0=0\end{aligned}
よって、右辺第1項の積分結果は0になる。第2項分の積分を考えれば良く、ガウスの発散定理を用いると
\begin{aligned}\int_{S_{2}}\boldsymbol{A} \cdot d\boldsymbol{S}&=\int_{V}\mathrm{div} \boldsymbol{A} dV \\ &= 4\pi*3 \\ &=12\pi\end{aligned}