指数分布関数の期待値、分散、確率の計算問題

問題

下記の指数分布関数を考える。なお、\(x\)は連続確率変数とし、\(\lambda \geq 1\)とする。

\begin{aligned}f(x)=\begin{cases}\lambda e^{-\lambda(x+2)} \qquad (x \geq -2) \\ 0 \qquad (x \leq -2)\end{cases}\end{aligned}

問1：\(X\)の期待値と分散を求めよ。
問2：\(X\)の値が負となる確率を求めよ。
問3：上記の確率密度関数に従う試行を10回試行したとき、負の値が2回以上出現する確率は0.99以上か。

はじめに
確率密度関数の期待値と分散の計算
指数分布とは
解答例

はじめに

電気情報系の大学院入試で確率統計が出題されるときは、大きく分けて2通りの問題構成になっていることが多いです。

確率統計の頻出分野

離散確率変数における期待値、分散、条件付き確率 (コイントス)
連続確率分布における期待値、分散、条件付き確率 (本記事で紹介)

離散確率変数については、大学受験で山ほど演習したと思います。確率漸化式を解く場合もありますが、その時の知識である程度の点が取れちゃいます。

一方で、連続確率分布に関しては大学で初めて出てきます。離散確率では、各事象に対しての確率をケーススタディで足し算していくだけだったのに対し、連続確率の場合は積分が必要です。このギャップが躓きやすいポイントになります。

一方で、巷の専門書やネットの記事では、残念ながら演習に関わる記事が少ないように感じます。

そこで、本記事では、確率密度関数の基本的な扱いについて紹介していこうと思います。指数分布を題材に扱っていますが、他の分布関数についても後段の記事で扱う予定です。

確率密度関数の期待値と分散の計算

確率密度関数を\(f(x)\)、確率変数を\(X\)とすると、下記の計算式で表されます。

期待値：\begin{aligned}E[X]=\int^{\infty}_{-\infty}xf(x)dx\end{aligned}
分散：\begin{aligned}V[X]=E[X^{2}]-(E[X])^{2}\end{aligned}
ただし、\(E[X^{2}]=\int^{\infty}_{-\infty}x^{2}f(x)dx\)

なぜこうなるのか？の厳密な説明は、市販の参考書に譲ります。ただ、離散確率の場合と同じ考え方です。期待値は、その時の確率と値の積を各場合の数に対して足し合わせていくことを積分で表現していますし、分散についても(2)式は離散確率に対しても用います。

上式を用いて問1を解いていきます。

問2は、確率密度変数が負の範囲を積分すればよく、問3は高校数学でも出て来た二項分布を考えれば良いです。

指数分布とは

解答例に移る前に簡潔に話します。待ち時間や寿命など、現実世界である事象が起こるまでの時間を数学的に表現した確率分布になります。

\begin{aligned}f(x)=\lambda e^{-\lambda x} \qquad (x \geq 0)\end{aligned}

で表されることが多く、負の領域では0です。これは、現実世界で過去に何かが発生する確率を現在から表現できないためです。

※問題文では、少し難しく\(x\)がオフセットした表記になっています。

λの大きさごとに、下記の確率分布になります。

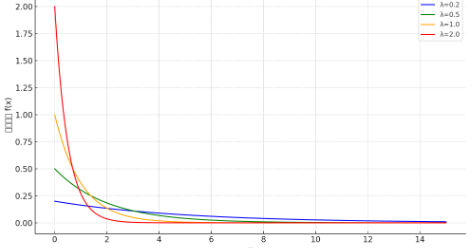
解答例

問1 期待値と分散

\(Y=X+2\)とすると、下記のように確率密度関数を変換できる。

\begin{aligned}f(y)=\lambda e^{-\lambda y} \quad (y \geq 0)\end{aligned}

上式を(2)式に代入すると、求める期待値\(E[Y]\)は

\begin{aligned}E[Y]&=\lambda \int^{\infty}_{0}y e^{-\lambda y}dy \\ &=\lambda \left \lbrack-y\dfrac{e^{-\lambda y}}{\lambda} \right \rbrack^{\infty}_{0}+\int^{\infty}_{0}e^{-\lambda y}dy \\ &=\dfrac{1}{\lambda}\end{aligned}

同様に、(4)式を(3)式に代入し、求める分散\(V[Y]\)は

\begin{aligned}E[Y^{2}]&=\lambda \int^{\infty}_{0} y^{2} e^{-\lambda y} dy \\ &=-\lambda \left \lbrack y^{2}\dfrac{e^{-\lambda y}}{\lambda} \right \rbrack -2 \lambda \left \lbrack y \dfrac{e^{-\lambda y}}{\lambda^{2}} \right \rbrack^{\infty}_{0} +2 \dfrac{\lambda}{\lambda^{2}} \int^{\infty}_{0} e^{-\lambda y}dy \\ &=\dfrac{2}{\lambda^{2}}\end{aligned}

\begin{aligned}V[Y]&=E[Y^{2}]-(E[Y])^{2} \\ &=\dfrac{2}{\lambda^{2}}-\dfrac{1}{\lambda^{2}} \\ &= \dfrac{1}{\lambda^{2}}\end{aligned}

確率変数\(Y\)を\(X\)に変換し直す。

\begin{cases}E[X]=E[Y]-E[2] \\ V[X]=V[Y-2]=V[Y]\end{cases}

\begin{cases}E[X]=\dfrac{1}{\lambda}-2 \\ V[X]=\dfrac{1}{\lambda^{2}}\end{cases}

問2 \(X\)が負となる範囲

与えられた式より、xを範囲[-2,0]で積分すれば良く

\begin{aligned}P(X<0)&=\int^{0}_{-2} \lambda e^{-\lambda(x+2)}dx \\ &=\lambda \left \lbrack -\dfrac{e^{\lambda(x+2)}}{\lambda} \right \rbrack^{0}_{-2} \\ &=1-e^{-2\lambda}\end{aligned}