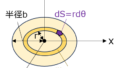
下記の系におけるポインティングベクトルを求め、エネルギーの流れについて考察せよ。
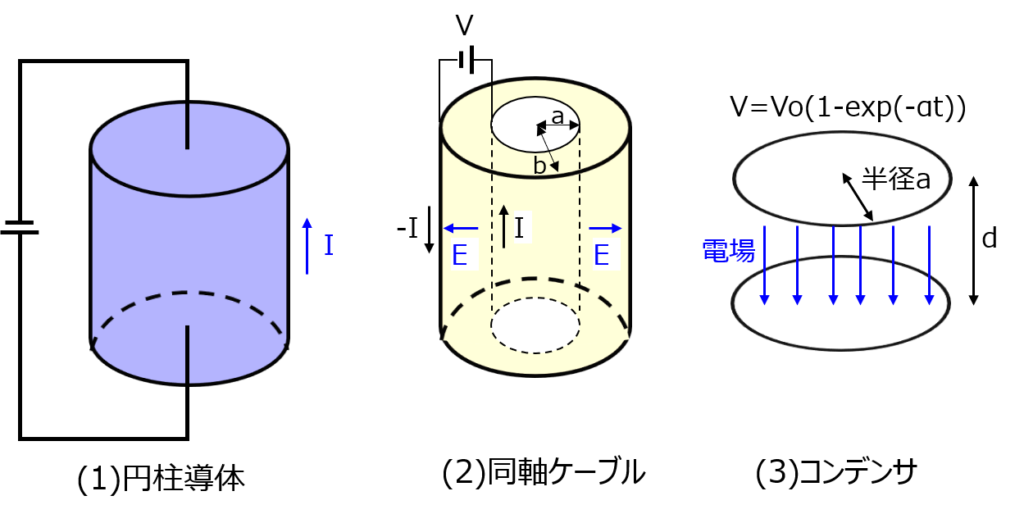
(1)半径\(a\)長さ\(l\)抵抗\(R\)の円柱導体の両端面に電圧\(V\)を印可し、電流\(I\)が一様に流れている系。
(2)内半径\(a\)、外半径\(b\)の無限長同軸ケーブルのそれぞれの表面に電流\(±I\)が流れており、両円筒間に電位差Vが生じている系。
(3)半径\(a\)の導体円盤を平行に配置したコンデンサに電圧を\(V=V_{o}(1-e^{-\alpha t})\)で印加している系。
ポインティングベクトルとは
題名から察するかもしれませんが、電磁エネルギーの流れを示すベクトルになります。
電場\(E\)と磁場\(H\)の外積を取り、下記で表されます。
\begin{aligned}\boldsymbol{S}=\boldsymbol{E}×\boldsymbol{H}\end{aligned}
あまり院試には出てこないですが、理解が深まるため、下記で導出をします。
導出
電磁エネルギー密度は、静電エネルギー密度\(u_{e}=\dfrac{\boldsymbol{E}\boldsymbol{D}}{2}\)と磁気エネルギー密度\(u_{m}=\dfrac{\boldsymbol{B}\boldsymbol{H}}{2}\)の和
\begin{aligned}u=\dfrac{\boldsymbol{E}\boldsymbol{D}}{2}+\dfrac{\boldsymbol{B}\boldsymbol{H}}{2}\end{aligned}
で表される。
一方で、電場と磁場の外積の発散に関して注目する。
\begin{aligned}div(\boldsymbol{E}×\boldsymbol{H})=\boldsymbol{H}・rot\boldsymbol{E}-\boldsymbol{E}・rot\boldsymbol{H}\end{aligned}
これに、下記のマクスウェル方程式を代入する。
\begin{cases}rot\boldsymbol{E}=-\dfrac{\partial \boldsymbol{B}}{\partial t} \\ rot\boldsymbol{H}=\boldsymbol{i}+\dfrac{\partial \boldsymbol{D}}{\partial t}\end{cases}
すると、下記のように式変形できる。
\begin{aligned}div(\boldsymbol{E}×\boldsymbol{H})=-\left ( \boldsymbol{E}・\dfrac{\partial \boldsymbol{D}}{\partial t}+\boldsymbol{H}・\dfrac{\partial \boldsymbol{B}}{\partial t}\right)-\boldsymbol{E}・\boldsymbol{i} \\ div(\boldsymbol{E}×\boldsymbol{H})=-\dfrac{1}{2}\dfrac{\partial}{\partial t}(\boldsymbol{E}・\boldsymbol{D}+\boldsymbol{B}・\boldsymbol{H})-\boldsymbol{E}・\boldsymbol{i} \end{aligned}
上式のうち、右辺の第1項は単位体積当たりの電磁エネルギーの減少率。第2項はジュール熱によるエネルギー損失になります。
その分を補填する形で、左辺の\(div(\boldsymbol{E}×\boldsymbol{H})\)がエネルギーを供給しているはずだ!とみなせるわけで、これをポインティングベクトル\(\boldsymbol{S}\)で一文字で表現しようというわけですね。
問題の解法
基本的に、ポインティングベクトルの流れを考える問題で、目新しい系はあまり出てきません。同軸ケーブル(円柱)か、コンデンサで問われることが多いです。
ですので、今までの単元で学んできた通り、電場\(E\)と磁場\(H\)をガウスの法則、アンペールの法則を用いて求め、その外積を取る作業に終始すれば良いです。
解答例
(1)両端の電位差がVの円柱
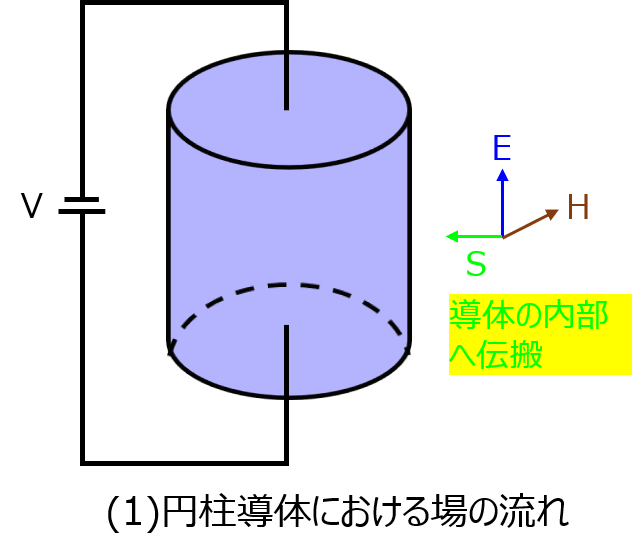
電場\(E\)の大きさは、単位体積当たりの電位差を指している。(向き:+z方向)
\begin{aligned}E=\dfrac{V}{l}=\dfrac{RI}{l}\end{aligned}
磁場の大きさは、アンペールの法則より、半径\(r=a\)の円を考えて
\begin{aligned}H=\dfrac{I}{2 \pi a}\end{aligned}
なお、向きは周方向である。
求めるポインティングベクトル\(S\)は、\(E\)と\(H\)の外積を取れば良い。フレミング左手の法則より、導体の内側に対し流れる。
\begin{aligned}|\boldsymbol{S}|=\dfrac{RI}{l}\dfrac{I}{2 pi a}=\dfrac{RI^{2}}{2 \pi al}\end{aligned}
これを円柱の側面積\(2 \pi a l\)に対して面積分すると、\(RI^{2}\)となる。よって、外部から供給された電力は、導体側面から内部へ流入し、ジュール熱になることを意味する。
(2)同軸ケーブルのエネルギーの流れ
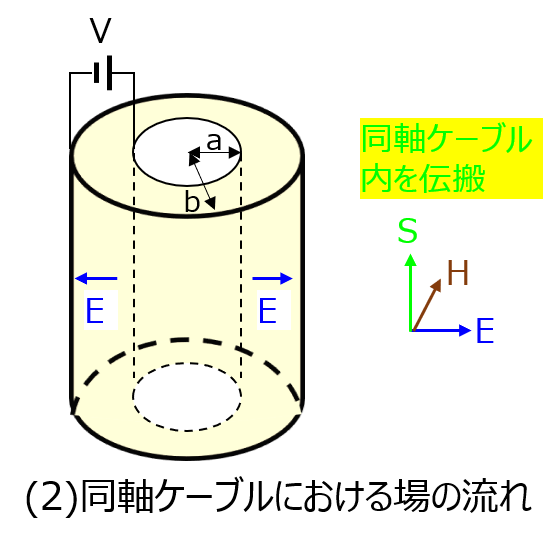
同軸ケーブルの内径に電荷Q、外径に電荷-Qを与えたとする。
ガウスの法則により、求める電場は
\begin{aligned}E=\dfrac{q}{2 \pi \varepsilon_{o}r}\end{aligned}
内径と外径の電位差\(V\)は
\begin{aligned}V=\dfrac{q}{2 \pi \varepsilon_{o}}\log\dfrac{b}{a}\end{aligned}
これより、電場の大きさは、問題文で与えられている定数を用いて
\begin{aligned}E=\dfrac{V}{r \log\dfrac{b}{a}}\end{aligned}
次に、磁場\(H\)は、アンペールの法則により
\begin{aligned}H=\dfrac{I}{2 \pi r}\end{aligned}
電場Eは径方向、磁場Hは周方向を向くので、ポインティングベクトルSはz方向を伝わる。その大きさは
\begin{aligned}|\boldsymbol{S}|=EH=\dfrac{VI}{2 \pi r^{2} \log\dfrac{b}{a}}\end{aligned}
これを、半径a<r<bの円の領域で面積分すれば
\begin{aligned}P&=\int^{b}_{a}\dfrac{VI}{2 \pi r^{2}\log\dfrac{b}{a}}2\pi r dr \\ &=VI\end{aligned}
よって、電源から供給されたエネルギーVIは同軸ケーブル内を減衰することなくz方向に伝搬していく。
(3)コンデンサ内のエネルギーの流れ
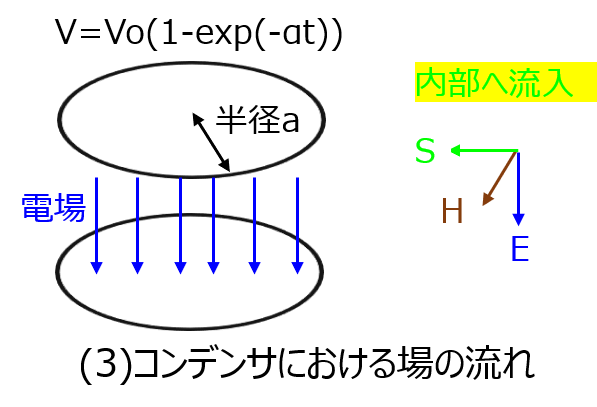
コンデンサ内には変位電流\(\left | \dfrac{\partial D}{\partial t} \right|\)が流れています。これを利用し、磁場\(H\)を求めます。
極板間の距離dのため、コンデンサ内の電場\(E\)、電束密度\(D\)は
\begin{cases}E=\dfrac{V_{o}(1-e^{-\alpha t})}{d} \\ D=\dfrac{\varepsilon_{o}V_{o}(1-e^{-\alpha t})}{d}\end{cases}
変位電流は、下記で求められる。
\begin{aligned}\left | \dfrac{\partial D}{\partial t} \right|=\dfrac{\varepsilon_{o}V_{o}\alpha}{d}e^{-\alpha t}\end{aligned}
これより、磁場Hは、アンペールの法則を変形して(半径r)
\begin{aligned}\int_{c}\boldsymbol{H}・d\boldsymbol{s}=\int_{S}\dfrac{\partial \boldsymbol{D}}{\partial t}・d\boldsymbol{S}=\left | \dfrac{\partial D}{\partial t} \right|\pi r^{2} \end{aligned}
\begin{aligned}H=\dfrac{\varepsilon_{o}\alpha V_{o}e^{-\alpha t}}{2d}r\end{aligned}
以上より、ポインティングベクトルの大きさは
\begin{aligned}S=EH=\dfrac{\varepsilon_{o}\alpha V_{o}^{2}e^{-\alpha t}(1-e^{-\alpha t})}{2d^{2}}r\end{aligned}
\(r=a\)のコンデンサ端で、ポインティングベクトルを面積分すれば
\begin{aligned}\int_{S}\boldsymbol{S}・d\boldsymbol{S}&=\dfrac{\varepsilon_{o}\alpha V_{o}^{2}e^{-\alpha t}(1-e^{-\alpha t})}{2d^{2}}a・2 \pi a d\\ &=\dfrac{\pi \varepsilon_{o} \alpha V_{o}^{2}e^{-\alpha t}(1-e^{-\alpha t})}{d}a^{2}\end{aligned}
ここで、\(I=C\dfrac{\partial V}{\partial t}\)の関係より
\begin{aligned}I=\dfrac{\pi \varepsilon_{o} \alpha V_{o}e^{-\alpha t}(1-e^{-\alpha t})}{d}a^{2}\end{aligned}
(21)式は(20)式の結果に対し\(V_{o}\)を割り算した結果に等しい。逆に、(20)式は
\begin{aligned}\int_{S}\boldsymbol{S}・d\boldsymbol{S}&=VI\end{aligned}
と表すことができる。電源から供給されたエネルギーVIは、コンデンサの側面から内部に流入していることが分かった。
最後に
ポインティングベクトルに関する問題は、様々な大学の院試で出題されます。上記の典型パターンは、それぞれ計算量が多いため、段取りを覚えておくことを推奨します。