確率変数\(X\)の確率密度関数が\(f(x)=\exp \lbrace -(ax^{2}+bx+c)\rbrace\)で与えられている。但し、\(a,b,c\)は実数で、\(a>0\)とする。
問:\(X\)の期待値\(E(X)\)と分散\(V(X)\)を\(a,b,c\)を用いて表せ。
ただし、下記の公式を用いて良い。
\begin{cases}\int^{\infty}_{-\infty}\exp(-ax^{2})=\sqrt{\dfrac{\pi}{a}} \\ \int^{\infty}_{-\infty}x^{2}\exp(-ax^{2})=\dfrac{1}{2a}\sqrt{\dfrac{\pi}{a}}\end{cases}
広島大学大学院 2022/8 確率統計より抜粋。公式を追加。
ガウス分布とは
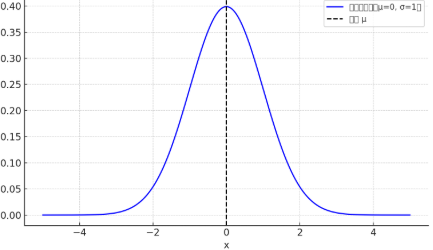
平均値\(\mu\)を中心とした、鐘型の確率密度関数を言います。メーカーでは、部品の誤差をモデル化するために用いられることが多いです。
例)あるセンサの10年故障率は0.01% → 3σ(99.7%)の範囲外だから許容範囲内。など、モノの評価、解析を行ううえで使用します。
院試では、指数分布に比べると出題頻度が落ちます。ただし、メーカーへ就職してからの技術的な検討を行う際、よく出てくる分布になります。この機に覚えておきましょう。
問題に対しての解答方針は、以前の記事と変わりません。関数f(x)にxを乗算した値で期待値を求めます。また、f(x)にxの2乗を乗算した値を用いて分散を考えます。計算が大変なので、この記事を確認しておくことをオススメします。
解答例
E[X],V[X]を求める前段階
前章で与えられた式をいきなり求めるのは大変なので、確率密度関数\(f(x)\)を積分し、関係式を求めます。
まず、確率密度関数の定義域を全部積分すると、確率1になるから
\begin{aligned}\int^{\infty}_{-\infty}\exp\lbrace -(ax^{2}+bx+c)\rbrace dx =1\end{aligned}
exp項内部を平方完成し
\begin{aligned}-(ax^{2}+bx+c)=-a\left(x+\dfrac{b}{2a}\right)^{2}-\dfrac{b^{2}}{4a}+c\end{aligned}
だから、**式は
\begin{aligned}\int^{\infty}_{-\infty}\exp\left \lbrace -a\left(x+\dfrac{b}{2a}\right)^{2}-\dfrac{b^{2}}{4a}+c \right \rbrace dx =1 \end{aligned}
\(t=x+\dfrac{b}{2a}\)と変数変換する。xの積分範囲は[-∞,∞]であり、tに変数変換しても変わらない。
\begin{aligned}\int^{\infty}_{-\infty} \exp\left \lbrace -a t^{2}-\dfrac{b^{2}}{4a}+c \right \rbrace dt =1 \end{aligned}
(1)式を用いると
\begin{aligned}\exp\left(\dfrac{b^{2}}{4a}-c \right) \cdot \sqrt{\dfrac{\pi}{a}}=1\end{aligned}
期待値E[X]
\begin{aligned}E[X]=\int^{\infty}_{-\infty}x\exp\lbrace -(ax^{2}+bx+c)\rbrace dx \end{aligned}
を求める。平方完成の式変形を考えて
\begin{aligned}E[X]=\exp\left(\dfrac{b^{2}}{4a}-c \right)\int^{\infty}_{-\infty}x\exp\left \lbrace -a\left(x+\dfrac{b}{2a}\right)^{2} \right \rbrace\end{aligned}
\(t=x+\dfrac{b}{2a}\)と変数変換し
\begin{aligned}E[X]=\exp\left(\dfrac{b^{2}}{4a}-c \right)\int^{\infty}_{-\infty}\left(t-\dfrac{b}{2a}\right)\exp(-at^{2})dt\end{aligned}
\(\int^{\infty}_{\infty}t \exp(-at^{2})dt\)は奇関数なので積分結果は0。これに前問の結果を合わせて
\begin{aligned}E[X]&=\exp\left(\dfrac{b^{2}}{4a}-c\right)\cdot \left(-\dfrac{b}{2a}\right)\cdot \sqrt{\dfrac{\pi}{a}} \\ &=-\dfrac{b}{2a}\end{aligned}
分散V[X]
前段階として\(E[X^{2}]\)を求める。\(E[X]\)と同様にして
\begin{aligned}E[X^{2}]=\int^{\infty}_{-\infty}x^{2}\exp\left \lbrace -a\left(x+\dfrac{b}{2a}\right)^{2} \right \rbrace \exp\left( \dfrac{b^{2}}{4a}-c\right)dx \end{aligned}
同じく、\(t=x+\dfrac{b}{2a}\)と変数変換し
\begin{aligned}E[X^{2}]=\exp\left( \dfrac{b^{2}}{4a}-c\right)\int^{\infty}_{-\infty}\left(t-\dfrac{b}{2a}\right)^{2}\exp(-at^{2})dt\end{aligned}
問題文で与えられた式(2)により
\begin{aligned}E[X^{2}]&=\exp\left( \dfrac{b^{2}}{4a}-c\right)\left(\dfrac{1}{2a}+\dfrac{b^{2}}{4a^{2}}\right)\sqrt{\dfrac{\pi}{a}} \\ &=\dfrac{1}{2a}+\dfrac{b^{2}}{4a^{2}}\end{aligned}
\(V[X]=E[X^{2}]-(E[X])^{2}\)より
\begin{aligned}V[X]=\dfrac{1}{2a}\end{aligned}
定数項$c$は期待値、分散に影響を及ぼさないことが分かりました。
最後に
試験では、具体的な条件を与えて\(a,b,c\)の値を求める問題が続きましたが、単純な方程式で片付くため省略します。