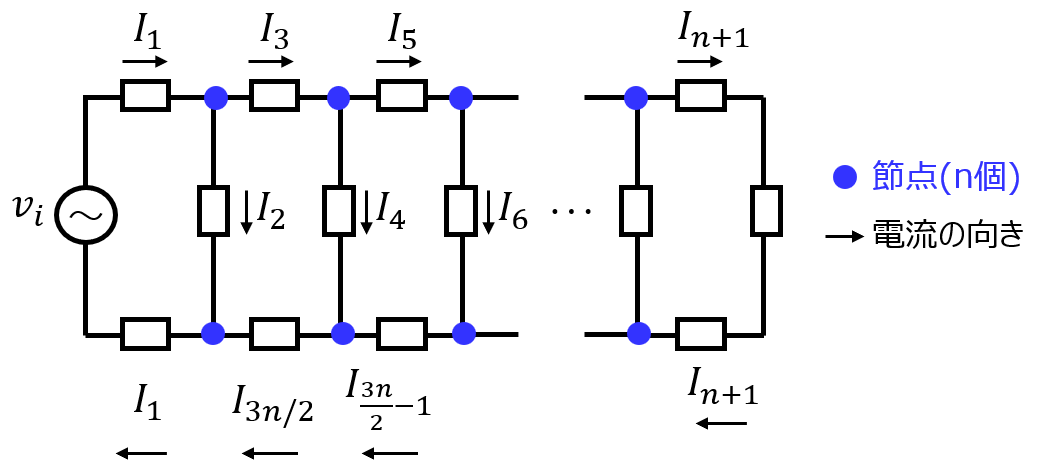
【問】図1に、節点数がn個の梯子型電気回路を考える。節点間の線(枝)ごとに電流変数\(I_{i} (i=1,2…n)\)を与える。入力端に電流源、電圧源を与えたとき、キルヒホッフの電流則及び電圧則で立式できる線形独立式の数をそれぞれ記せ。なお、回路パラメータの与え方は任意とする。
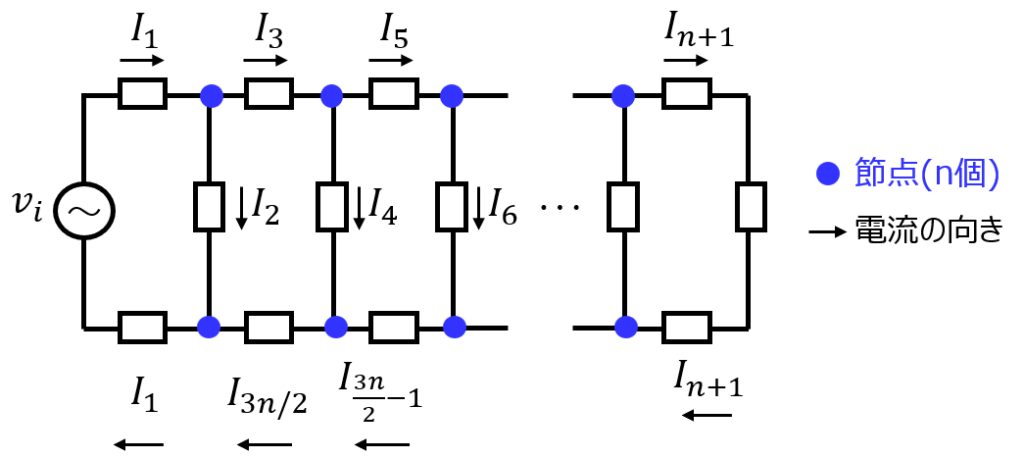
はじめに
電気回路の問題の解法として、「キルヒホッフの電流則と電圧則を連立し、未知変数の値を求める」やり方は中学高校から行ってきたことだと思います。
大学でもその方針は変わりませんが、複雑な電気回路を与えられた際に立てる式に戸惑うことがあります。
例えば、問で与えられた電気回路は、n個の節点が存在するため、電流則をn個立式できると考えられます。
ですが、本当にn個全て線形独立で、変数を求める解くうえの立式が漏れなく必要なのでしょうか?
本記事では、電気回路を解くうえでほぼ必ず使用するキルヒホッフの電流則、電圧則の線形独立式の数をそれぞれ考えます。
この記事を通して覚えたいこと
線形独立式の数は、以下の関係になる。

特に主張したいことは、電流則で作成することができる線形独立式はn-1個という事実です。(グラフの形状によりn-2個以下になるかもしれませんが、試験問題で出される回路では、n-1個で立式することを基本線に考えて構わないと思います。)
本記事では、考え方を厳密に理解して欲しいということよりも、結果の暗記を重視いただきたいと考えています。
一応、下記に管理人なりの説明を記載しますが、興味が無い方は「この事実が役立つ場面」の項目までスクロール下さい。
実験を通した線形独立式の確認(電流則)
簡単化のため、梯子が4段の下記回路を考えます。
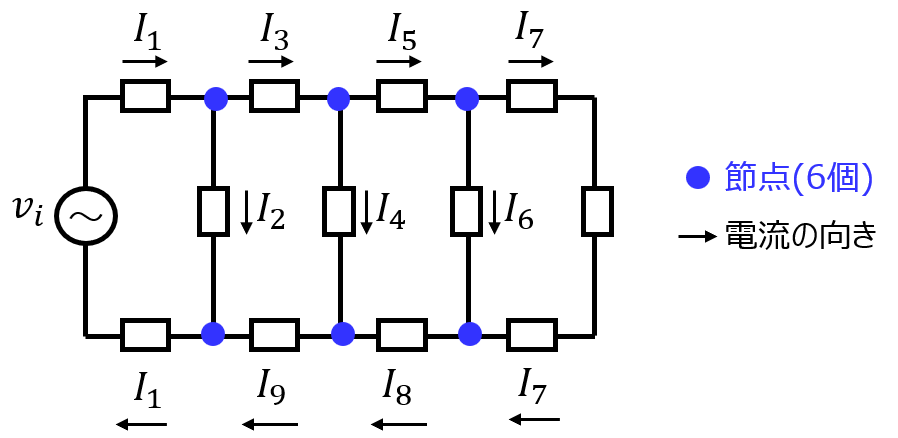
節点が6個あるわけですから、全ての節点分の式を連立してみます。
\begin{cases}I_{1}-I_{2}-I_{3}&=&0 \qquad ・・・(1) \\ I_{3}-I_{4}-I_{5}&=&0\qquad・・・(2) \\ I_{5}-I_{6}-I_{7}&=&0\qquad・・・(3) \\ I_{6}+I_{7}-I_{8}&=&0\qquad・・・(4) \\ I_{4}+I_{8}-I_{9}&=&0\qquad・・・(5) \\ I_2+I_{9}-I_{1}&=&0\qquad・・・(6)\end{cases}
それぞれの変数\(I_{i}\)正負の項が一つずつ存在するため、(1)~(6)全て足し合わせると、(左辺)=(右辺)=0となり、一次従属の行が存在していることが分かりました。式を連立して変数を求めていく上では、不要な式となります。
ここで、どれか一つの式を抜いた状態で他の式を足し合わせることを考えます。例えば、(5)を抜いて、(1)~(4)、(6)を足すことを考えます。
結果ですが、\(I_{9}-I_{4}-I_{8}=0\)となり、符号を反転すると式(5)を実現できることが分かりました。よって、ある一つの節点を抜いた状態でも回路全体の節点それぞれで入出力する電流の関係を表現することができました。(線形独立)
これは、任意のn個の節点を持つ回路に対しても同じで、1つの式の分は独立にならず、連立できる式の数はn-1個であることが分かります。
グラフ理論から見る電流則の解釈
前章の結果は、グラフ理論から見ると、下記の話に置き換えることができます。
- 連立方程式で立式した式のみでグラフを書くことを考える。
- このとき、任意の一点に関する式を使用しなくとも、グラフの復元は可能である。
- もし、全ての点を連立してしまうと、どれか1つは条件として冗長であり、グラフの復元には不要である。(一次従属)
例として、式(5)(真ん中下の節点抜き)でグラフの復元を試みます。式(1)が表す節点から順にグラフを書いていきます。
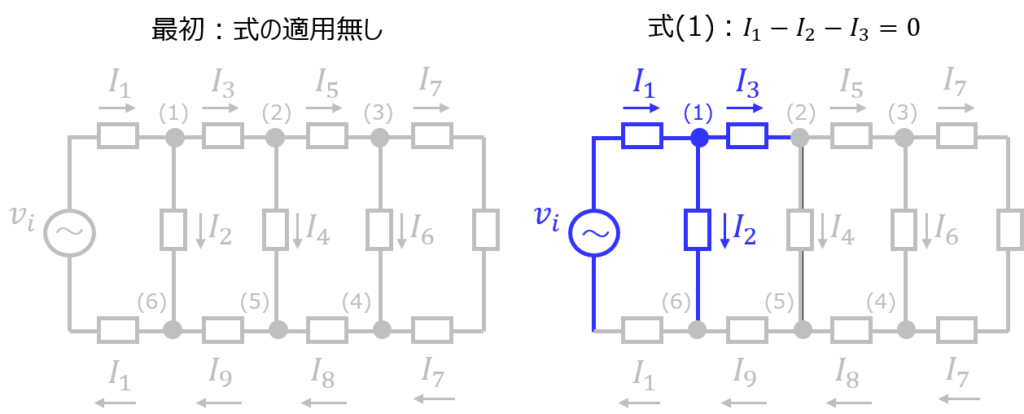
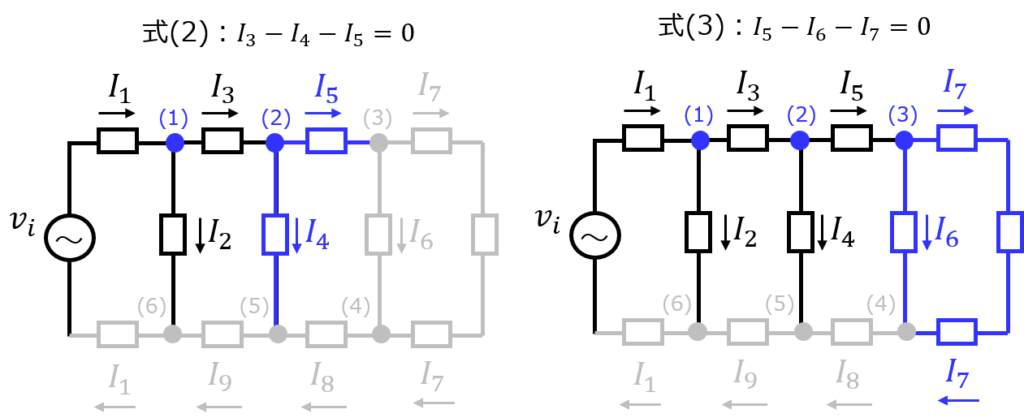
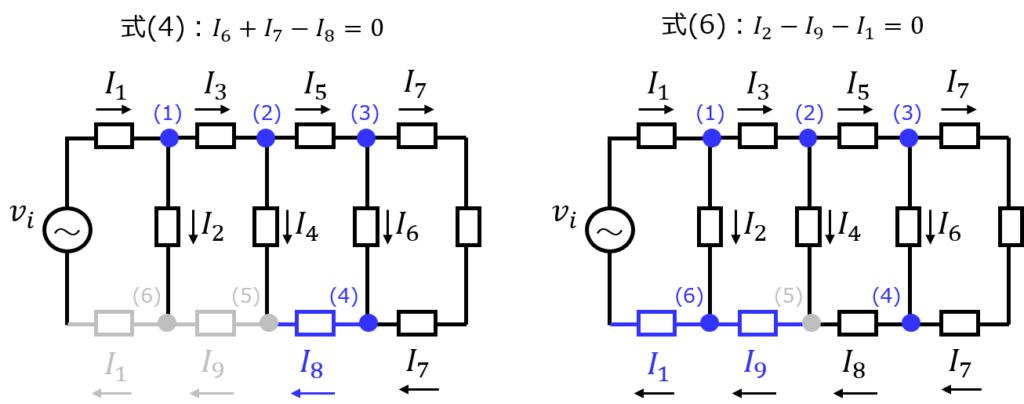
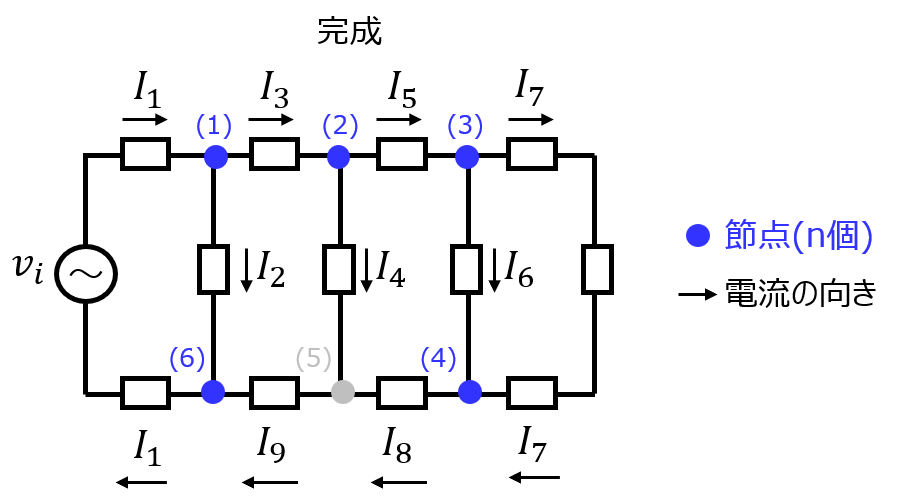
問題無く復元できることが分かりました。
式(1)~(4)、(6)を連立していれば、式(5)は不要になる前章の話と一致しています。
結局、電流則の数学的な意味は、与えられた回路の節点の性質を式に落とし込んでいることに他なりません。
これが、任意のグラフにおいて成立するため、電流則で立式可能な線形独立式の数がn-1個であることが、視覚的にも理解することができました。
こちらは、ソースが電流源の場合でも電圧源の場合でも同様に成立すると考えられます。
節点における電流の出入りに注目した立式のため、そこに入力元のソースの素性は関係ないからです。
実験を通した線形独立式の確認(電圧則)
続いて、電圧則を考えてみます。こちらは、ソースによって立式できる数が変わります。
(i)電流源の場合:
重ね合わせの理より、電流源は開放する。すると、下記のようなグラフが出来上がる。
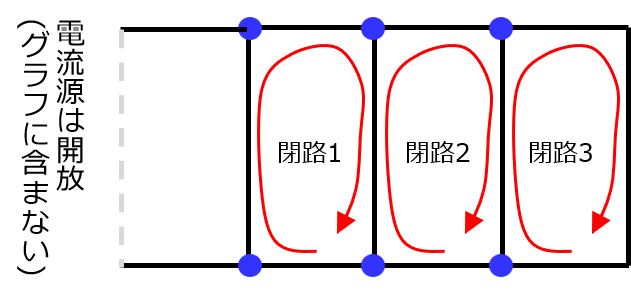
3つ独立な閉路を取ることができる。
(ii)電圧源の場合:
重ね合わせの理より、電圧源は短絡する。すると、下記のようなグラフが出来上がる。

4つ独立な閉路を取ることが出来る。
この事実から、ソースが電圧源の場合、立式できる線形独立式の数は、電流源に対して一つ多いことが分かりました。
電圧源のときと電流源のときで、線形独立式の総数が1つ異なるようになります。(変数の総数)=(線形独立式の総数)のはずなのに、この分はどこから出てくるのか?という疑問が次に生まれます。
こちらは、下記の考え方で解決することができます。
電流源Jがソースのときは、入力端が\(I_{1}=J)\となり、求める変数が一つ少なくなる。変数が1つ減るため、線形独立式が1つ減っても変数の数と同数になる。
一方で、電圧源がソースのときは、入力端\(I_{1}\)が未知数のままですが、電圧則によって立式できる式が1つ増えることにより、変数と線形独立式の数が同数になる。
グラフ理論から見る電圧則の解釈
電流則は節点に注目するのに対し、電圧則は閉路に注目します。
電流則と同じく、電圧則で回路を復元することを考えます。
まず、最小全域木を考えます。定義から、閉路は存在しないです。逆に、どれか1つ枝を追加すると、閉路が出来上がり、その分電圧則を立式できることが分かります。
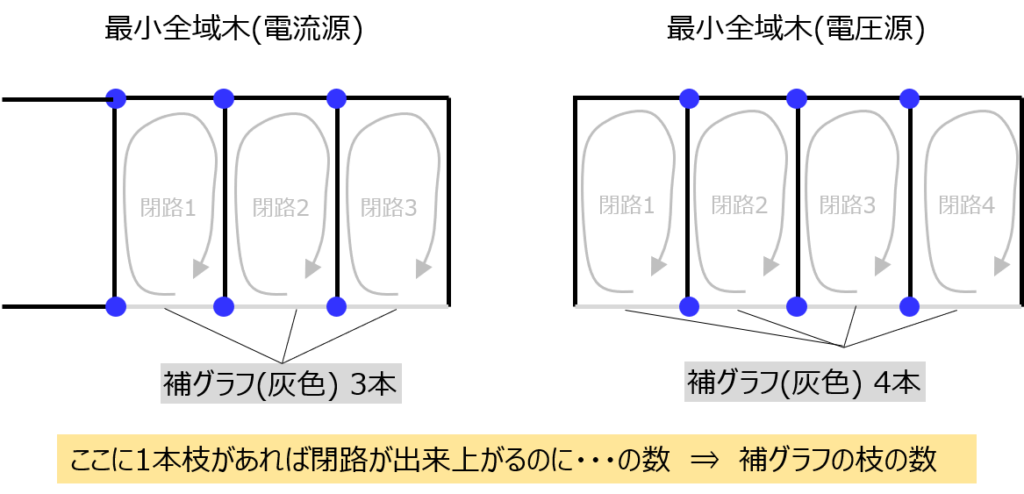
これが、最小全域木には含まれていない補グラフの枝全てにあてはまるため、(最小全域木の補グラフの枝の数)=(電圧則で立式できる式の数)であることが分かります。
※電流源の場合は、繋がっている枝が初めから存在しない状態を考えるため、電圧源に対して枝の数が1つ少なくなります。この関係から、立式できる線形独立式の数が1つ少ないことが、グラフからも説明できました。
この事実が役立つ場面
電気回路網の数値解析を行う際に役立ちます。
1.電気回路でメッシュを切り、各枝に電流変数を設定
2.電流則、電圧則の式を線形独立分連立し、行列演算によりそれぞれの電流変数を求める。
こちらで計算することは可能ですが、ここでやりがちなのが、電流則で余計な分の式1つを連立してしまい、電圧則で連立すべき式が1つ抜けているミスです。
節点がn個あるからといって、電流則をそのままn個連立しても正しい答えは返ってきません。
このミスに気付かないまま解析してしまうと、ドツボにはまってしまいます。
解析時間幅を短くしてみたり、メッシュを切りなおして回路定数の精度を高めるなどの対策を行ってしまいがちですが、そもそもの立式を間違えていると、どうしようもありません。
知っていれば防げるミスを知らないがために、時間を無駄にしてしまうことが無いように、こちらの記事を作成しました。
資格試験では、このような複雑な回路が出てくる可能性は低いですが、是非冒頭で紹介した事実を抑えておいて、正しくスムーズに立式できるようにしたいですね。
参考文献
大学課程 電気回路(1) 大野 克郎(著)、西 哲生(著) 第7章