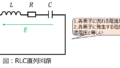【院試頻出】テブナンの定理を利用した供給電力最大則

供給電力最大則とは

文字を読んでのごとく、抵抗で消費する電力を最大化する条件です。

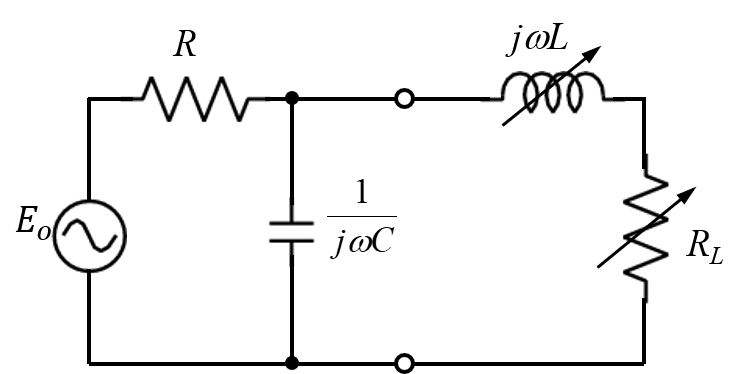
例として、下記の回路を考えます。\(R_{o},X_{o}\)は常時一定、\(R_{L},X_{L}\)は条件によって可変/一定になります。

(i)抵抗\(R_{L}\)が可変、(ii)リアクタンス\(X_{L}\)が可変、(iii)両方可変の3パターンありますが、下記の式を基本として消費電力の最大を考えます。

\begin{eqnarray}R_{o}+jX_{o}=R_{L}-jX_{L}\end{eqnarray}

簡単に言えば、可変抵抗値は一定抵抗値と等しく、リアクタンスは、一定値側と逆向きに同じ値を持っていれば消費電力最大になります。

抵抗値が小さすぎると、回路に流れる電流値は増えるものの、有効電力\(P=RI^{2}\)の\(R\)項が小さすぎてあまり電力消費しません。逆に抵抗が大きすぎると、回路に流れる電流値が小さすぎてあまり電力消費しません。トレードオフの関係になっていますが、ちょうど良い地点が\(R_{o}=R_{L}\)というわけですね。

一方で、リアクタンスについては簡単に説明できます。回路全体のリアクタンスが\(Im(Z)=X_{o}+X_{L}\)で表されますが、0に近づいた方が力率が大きくなります。よって、\(X_{o}=-X_{L}\)の関係式が導かれます。

(i)Rが可変のとき

(1)式を理解できれば導出不要かもしれませんが、一応記載していきます。

(1)式を(変数項)=(定数項)の関係式になるように変形して

\begin{eqnarray}R_{L}=R_{o}+jX_{o}+jX_{L}\end{eqnarray}

これの絶対値を取ることで、下記の条件のとき、消費電力最大になる。

\begin{eqnarray}R_{L}=R_{o}+\sqrt{(X_{o}+X_{L})^{2}}\end{eqnarray}

電源から右を見た時の回路インピーダンスに等しいように可変抵抗\(R_{L}\)を選ぶことを意味しています。

こうすると、前章でお話ししたように、有効電力\(P=RI^{2}\)において、RもIも小さすぎず、最適設計できます。

(ii)Lが可変のとき

(1)式の虚部を相殺するように\(X_{L}\)を設定するので

\begin{eqnarray}X_{L}=-X_{o}\end{eqnarray}

のとき、有効電力最大になります。リアクタンス項が無くなるので

\begin{eqnarray}P=\dfrac{R|E|^{2}}{(R_{o}+R_{L})^{2}}\end{eqnarray}

と表すことができます。

(iii)R、Lが可変のとき

これは簡単です。(i)、(ii)の組み合わせで

\begin{eqnarray}R_{L}=R_{o},X_{L}=-X_{o}\end{eqnarray}

のとき、有効電力\(P\)は最大になります。(複素共役)

このとき

\begin{eqnarray}P=\dfrac{|E|^{2}}{4R_{o}}\end{eqnarray}

と表すことができます。

テブナンの定理と組み合わせた供給電力最大則

回路構成によっては、前章までの条件をそのまま代入すれば答えが出ます。

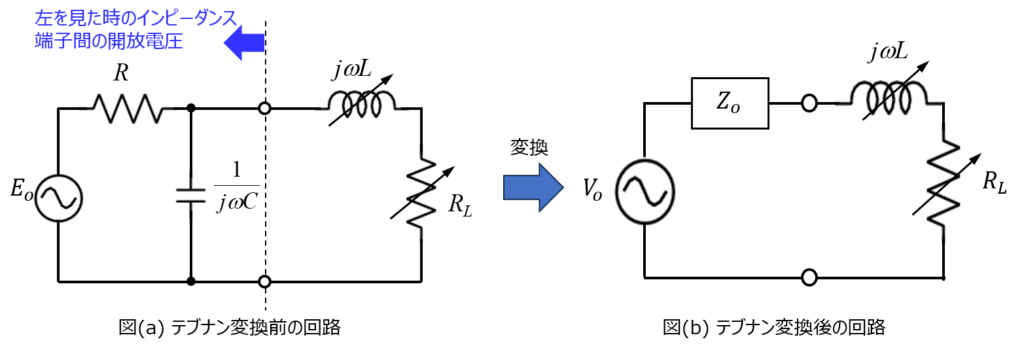
しかし、冒頭で紹介した問題(図(a))は、電源電圧と並列にコンデンサが挟まっています。よって、図(b)のような構成になっていないです。

これを図(a)の形になるよう変換しなければなりません。このとき、テブナンの定理を使用します。

テブナンの定理を利用すると、回路上の任意の2点から内部を見るときは、ある起電力と内部インピーダンスを持つ電源に変換することができます。

これを図(a)の回路において、定数部分と可変抵抗部分の間に2点を取り、内部インピーダンス\(Z_{o}\)と2点間を開放したときの電圧\(V_{o}\)を考えます。

\begin{aligned}Z_{o}&=\dfrac{\dfrac{R}{j \omega C}}{R+\dfrac{1}{j \omega C}} \\ &= \dfrac{R}{1+j \omega CR} \end{aligned}

\begin{aligned}V_{o}= \dfrac{E}{1+j \omega CR} \end{aligned}

これにより、図(a)の回路も、図(b)と同じ形に出来ました。あとは、供給電力最大則に当てはめると答えは出ます。

解答

R、Lが可変のとき、\(Z_{o}\)と複素共役になっていれば良い。

\begin{cases}R_{L}=\dfrac{R}{1+\left( \omega CR\right) ^{2}}\
L=\dfrac{CR^{2}}{1+\left( \omega CR\right) ^{2}}\end{cases}

このときの有効電力は、回路全体のリアクタンス成分が0なので

\begin{eqnarray}P=\dfrac{V^{2}}{4R_{L}}=\dfrac{E^{2}}{4R_{o}}\end{eqnarray}

最後に

本問は、大学院入試でよく出題されます。電通大、広島大辺りはこの辺りの問題。もう少し上の大学は回路構成が複雑になったりしますが、基本的な考え方は変わりません。

地道に計算して得点できるようにしましょう。