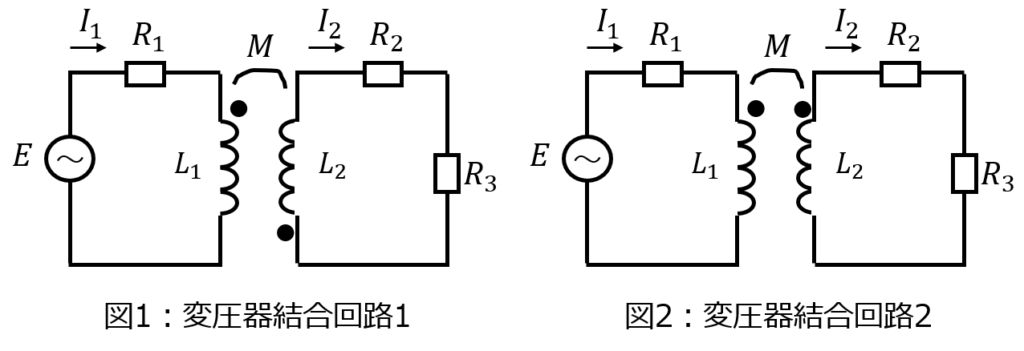
下記の変圧器結合回路(図1~4)を考える。次の問いに答えよ。
(1)図1,2の回路において、一次側、二次側の回路方程式をそれぞれ立てよ。
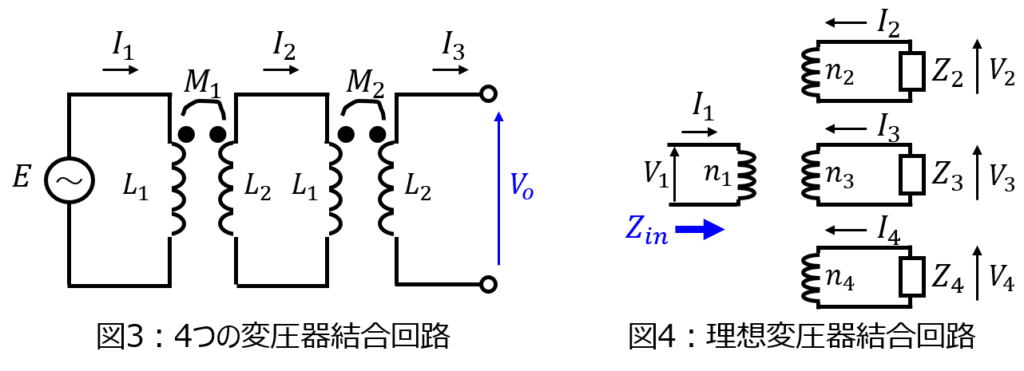
(2)図3の回路において、出力端の電圧\(V_{o}\)を求めよ。
(3)図4の回路において、変圧器1から見た入力インピーダンス\(Z_{in}\)を求めよ。
変圧器結合回路とは
回路の1次側、2次側にコイルが存在し、相互インダクタンスによって磁気的に結合している回路を言います。(変”成”器等価回路とも言います。)
例えば、下記のように一次側がコイル\(L_{1}\)、二次側がコイル\(L_{2}\)、相互インダクタンス\(M\)の回路を考えます。
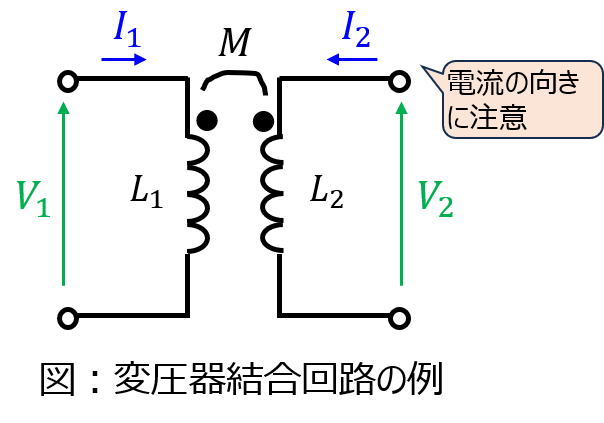
このとき、一次側、二次側に発生する電圧を考えます。
一次側に発生する電圧\(V_{1}\)は、自身のコイル\(L_{1}\)に流れる電流から発生する起電力\(L_{1}\dfrac{dI_{1}}{dt}\)と二次側で電流\(I_{2}\)が流れることによる誘導起電力\(M\dfrac{dI_{2}}{dt}\)の重ね合わせで決まるため
\begin{aligned}V_{1}=L_{1}\dfrac{dI_{1}}{dt}+M\dfrac{dI_{2}}{dt}\end{aligned}
で表されます。二次側にかかる電圧\(V_{2}\)も、添え字を1→2に変更し、同じ考え方により
\begin{aligned}V_{2}=M\dfrac{dI_{1}}{dt}+L_{2}\dfrac{dI_{2}}{dt}\end{aligned}
となります。回路的に導線で繋がっていませんが、磁気的につながっているため、一次側、二次側で発生する電圧は、もう一方のパラメータにも影響することが分かりました。
なお、電源電圧\(E\)を交流電圧源とすると、\(E=E_{o}e^{j \omega t}\)で表されることから
\begin{cases}V_{1}=j \omega L_{1}I_{1}+j \omega MI_{2} \\ V_{2}=j \omega MI_{1}+j \omega L_{2}I_{2}\end{cases}
になります。院試では、フェーザ回路の出題が多いため、上式の形で使うことが多いです。
変圧器結合回路の等価回路の変換
前節より、回路が物理的につながっていなくとも、磁気によって結合されていることが分かりました。となると、磁気の影響を何らかのパラメータで表し、物理的に繋がった回路でも仮想的に表すことができるはずです。
結論ですが、下記のようなT型回路に等価変換できます。相互インダクタンス\(M\)を回路の中央に配置し、回路の左右に元々あったインダクタ\(L_{1},L_{2}\)を\(L_{1}-M,L_{2}-M\)に置き換えることで達成できます。
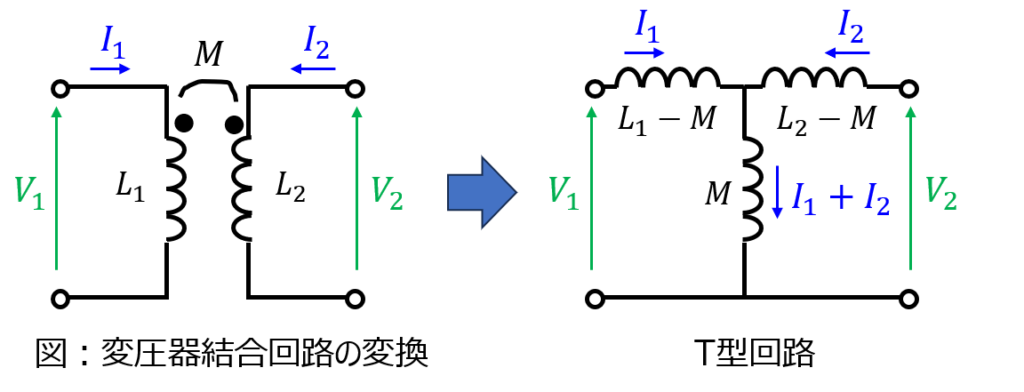
理由ですが、(3)式を変形することで分かります。
\begin{cases}V_{1}=j \omega (L_{1}-M)I_{1}+j \omega M(I_{1}+I_{2}) \\ V_{2}=j \omega M(I_{1}+I_{2})+j \omega (L_{2}-M)I_{2}\end{cases}
相互インダクタンス\(M\)項を無理やり電流\(I_{1},I_{2}\)の和にし、その差を自己インダクタンス項で補正してやることで変換後の回路を表現できることが数式的に分かりました。
複数個の変圧器の場合
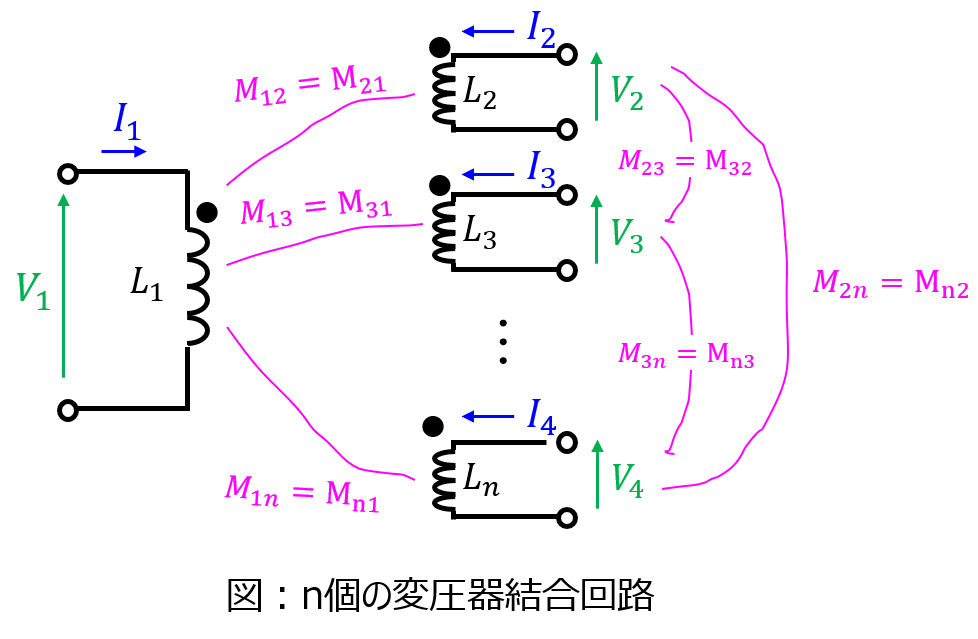
数式の数が多くなるだけでやることは同じです。変圧器1-2間の結合、1-3間の結合、1-n間の結合。2-1間、・・・2-n間の結合を順に考えれば良いです。
変圧器i,j間の相互インダクタンスを\(M_{ij}\)で表すと、各変圧器にかかる端子電圧\(V_{1},V_{2}\ldots V_{n}\)は
\begin{aligned}\begin{pmatrix}V_{1} \\ V_{2} \\ \vdots \\ V_{n}\end{pmatrix}=\begin{pmatrix} M_{11}M_{12} & \ldots M_{1n} \\ M_{21}M_{22} & \ldots M_{2n} \\ \vdots \vdots & \vdots \\ M_{n1} M_{n2} & \ldots M_{nn} \end{pmatrix}\begin{pmatrix}I_{1} \\ I_{2} \\ \vdots \\ I_{n}\end{pmatrix} \end{aligned}
になります。これは、電磁気学のノイマンの公式の考え方と通じます。
密結合変圧器とは
コイル1-2の間に流れる磁束が共通で、漏れ磁束が発生せず、相互インダクタンス\(M\)の2乗がそれぞれのコイルの自己インダクタンス\(L_{1},L_{2}\)の積に等しい変圧器を言います。
\begin{aligned}M=\sqrt{L_{1}L_{2}}\end{aligned}
で表され、結合係数kは1になります。(結合係数に関しては、こちらの記事で詳しく説明しています。)
このとき、(3)式は下記の関係になります。
\begin{cases}V_{1}=j \omega L_{1}I_{1}+j \omega MI_{2} \\ V_{2}=\dfrac{M}{L_{1}}V_{1}\end{cases}
この関係は、透磁率が大きい鉄心を利用することで近似的に実現できます。
このとき、コイル\(L_{1},L_{2}\)の巻き線比を\(n\)とすることで
\begin{aligned}V_{1}:V_{2}=L_{1}:M=M:L_{2}=1:n\end{aligned}
と表せます。これを(6)式に当てはめると、\(L_{1},M,L_{2}\)の関係は下記のようになります。
\begin{aligned}L_{1}:M:L_{2}=1:n:n^{2}\end{aligned}
理想変圧器について
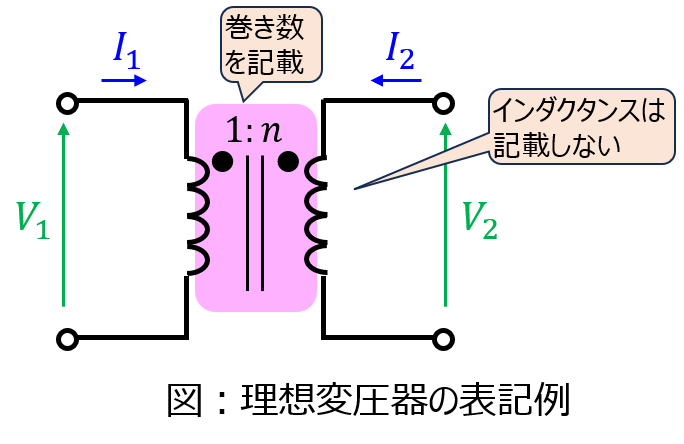
密結合変圧器において、エネルギーの損失が無く、磁気エネルギーを無限に蓄えられる変圧器を言います。回路上では、相互インダクタンス\(M\)は記載せず、それぞれのコイルの巻き数を記載することが多いです。
磁気の飽和状態に関して気にする必要は無くなるため、電圧、電流は純粋にコイル1,2の巻き線比に依存する形となります。
電圧は磁束に比例することから、コイルの巻き数に依存します。
今、ある電力\(P_{1}\)を一次側から二次側へ伝送するとき、一次側コイルと二次側コイルの巻き数比を\(n=\dfrac{N_{2}}{N_{1}}\)とすると、下記の式で表されます。
\begin{cases}nV_{1}=V_{2} \\ I_{1}+nI_{2}=0\end{cases}
電力は一定値なので、電圧が大きくなった分、電流が小さくなる関係にあります。
よって、電圧は巻線の数に比例し、電流は巻線の数に反比例することが分かりました。(問題を解くうえで大変重要です。必ず覚えましょう。)
損失に関する項が無いことから、理想変圧器に関して、下記の性質が分かります。
- 電力は理想変圧器を素通りし、消費、蓄積することは無い。
これは、(10)式に損失に関する項が無いことからも理解できます。問題で与えられている変圧器は、通常のものなのか、理想的なものであるのか、しっかりチェックするようにしましょう。
複数個の理想変圧器の場合
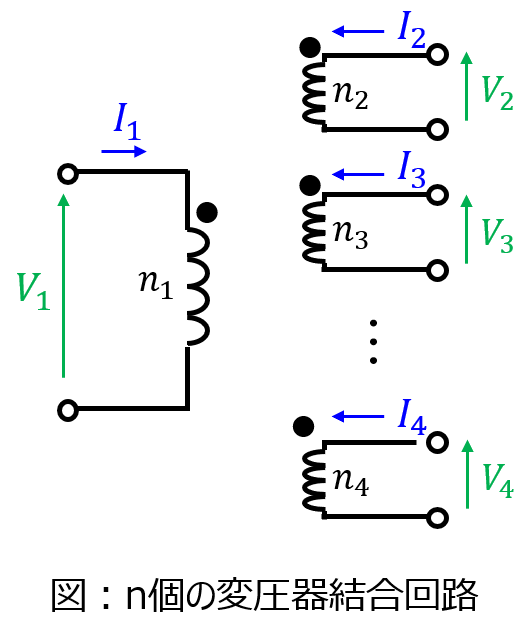
通常の変圧器と同様、変圧器1~nの間の相互作用を順に式で表していけば良いです。
理想変圧器の数をn個とすると、(10)式から下記で表されます。
\begin{cases}V_{1}:V_{2}:\ldots:V_{n}=n_{1}:n_{2}:\ldots:n_{n} \\ n_{1}I_{1}+n_{2}I_{2}+\ldots+n_{n}I_{n}=0\end{cases}
問題を解く際の注意点
ここまで説明すると、基本的に(3)式を暗記して問題を解けばいいじゃん!となりそうですが、留意すべき点があります。コイルの極性です。
極性とは、誘導起電力の向きです。電気回路では、黒点●で表されることが多く、電流が黒点の向きに流れると正の誘導起電力が発生する。と考えます。
このとき、わざわざ黒点と逆向きに電流を設定する意地悪な問題が散見されます。この場合、(3)式の項は負になります。
極性に気を付けないと正しく立式できず、得点できないことになります。解答に際しては、十分に気を付けましょう。実際に(1)で取り扱います。
解答例
(1)電流の向き、極性が異なる回路
図1の回路
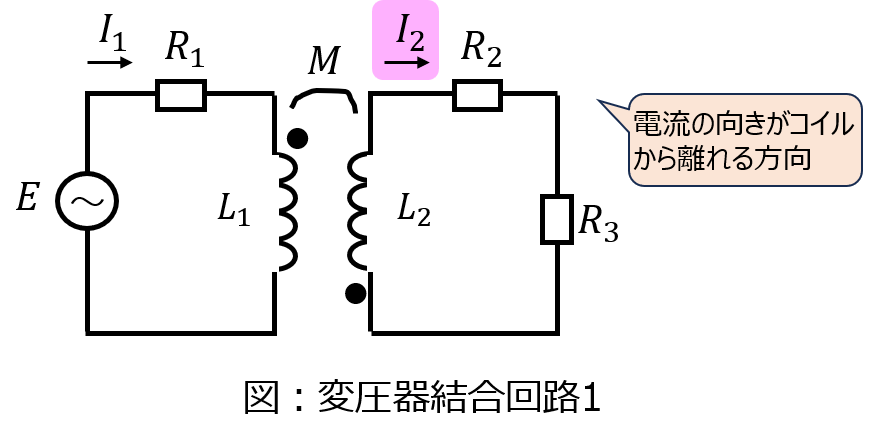
黒点が逆なので極性が異なるように見えますが、\(I_{2}\)の向きに注目すると、コイル黒点側から入るようになっています。よって、極性は前節で紹介した回路と同じです。相互インダクタンス\(M\)の正負は逆転しません。一方で、電流ベクトルの向き自体は前節と逆になっているので
\begin{cases}E=R_{1}I_{1}+j \omega L_{1} +j \omega M (-I_{2}) \\ R_{2}I_{2}=j \omega MI_{1}+j \omega M (-I_{2})\end{cases}
になります。相互インダクタンスの正負は逆転しないが、電流の正負が逆転します。
図2の回路
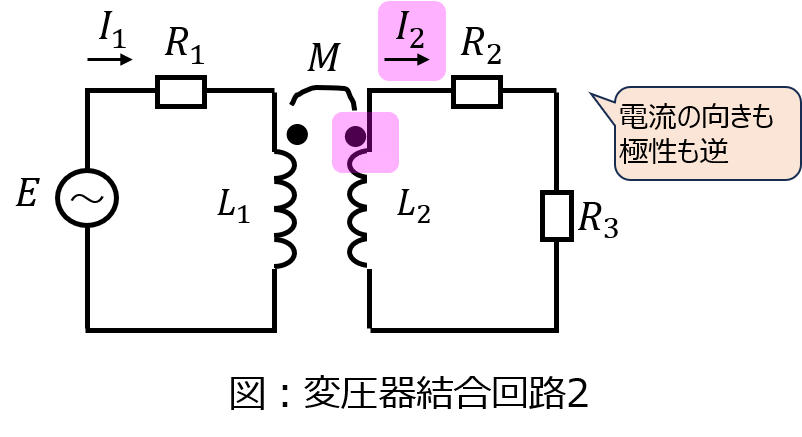
今度は、電流\(I_{2}\)は黒点の逆側から流れるようになります。よって、極性が逆になるので、相互インダクタンスは\(-M\)として考えます。
一方で、電流ベクトル\(I_{2}\)の向きは、図1に続いて前節と逆向きに流れているので
\begin{cases}E=R_{1}I_{1}+j \omega L_{1} +j \omega (-M) (-I_{2}) \\ R_{2}I_{2}=j \omega MI_{1}+j \omega (-M) (-I_{2})\end{cases}
結局、右辺の項は全て正となります。ただし、極性も電流の向きも逆だから、逆転の逆転で結果的に正になるという思考過程になります。
(3)式を丸暗記して、全ての項が正になるように立式したら、結果的に正解してしまった。とならないように気を付けましょう。(このようなミスは減点対象となりやすいです。)
(2)4つの変圧器で結合した回路
T型等価回路により、下記のように変換できる。
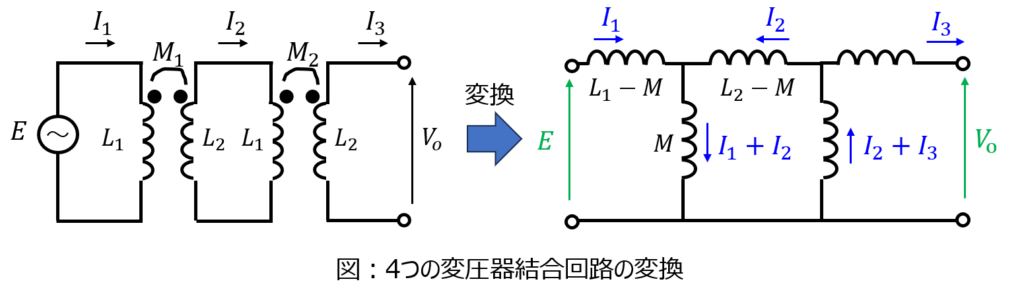
電流\(I_{1},I_{2},I_{3}\)を図の向きに設定し、回路方程式は
\begin{cases}E=j \omega (L_{1}-M)+j \omega M_{1}(I_{1}+I_{2}) \\ 0=j \omega M_{1}(I_{1}+I_{2})+j \omega (L_{2}-M_{1})I_{2}+j \omega (L_{3}-M_{2})I_{2}+j \omega M_{2}I_{2} \end{cases}
これを簡単にすると
\begin{cases}E= j \omega L_{1}I_{1}+j \omega M_{1} I_{2} \\ 0=j \omega M_{1}I_{1}+j \omega L_{2}I_{2} + j \omega L_{3}I_{2}\end{cases}
上式を解いて
\begin{aligned}I_{2}=\dfrac{ j \omega M_{1} E}{\omega^{2}\lbrace L_{1}(L_{2}+L_{3})-M^{2} \rbrace}\end{aligned}
出力端の電圧\(V_{o}\)は
\begin{aligned}V_{o}=j \omega M_{2} I_{2}\end{aligned}
だから、上記2つの式を連立することにより
\begin{aligned}V_{o}=\dfrac{M_{1}M_{2}E}{M^{2}-L_{1}(L_{2}+L_{3})}\end{aligned}
を得る。
(3)理想変圧器の入力インピーダンス
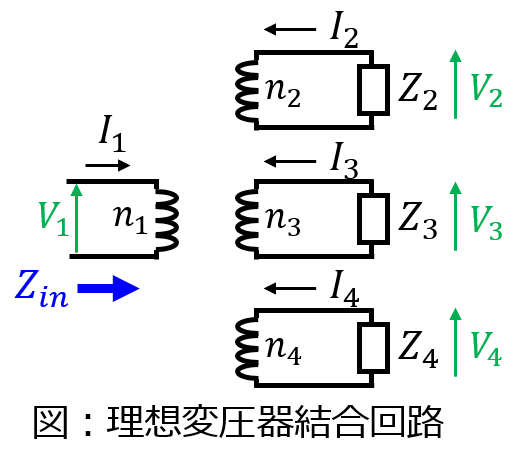
与えられたパラメータの向きに注意すると、(11)式により
\begin{aligned}n_{1}I_{1}=-(n_{2}I_{2}+n_{3}I_{3}+n_{4}I_{4}) \\ \dfrac{V_{1}}{n_{1}}=\dfrac{V_{2}}{n_{2}}=\dfrac{V_{3}}{n_{3}}=\dfrac{V_{4}}{n_{4}}\end{aligned}
電圧\(V_{2}\)に関して、\(V_{2}=-Z_{2}I_{2}\)だから
\begin{aligned}\dfrac{V_{1}}{n_{1}}=-\dfrac{Z_{2}}{n_{2}}I_{2} \\ I_{2}=-\dfrac{n_{2}}{n_{1}Z_{2}}V_{1} \end{aligned}
同様にして、\(V_{3},V_{4}\)に関しても
\begin{aligned}I_{3}=-\dfrac{n_{3}}{n_{1}Z_{3}}V_{1} \\ I_{4}=-\dfrac{n_{4}}{n_{1}Z_{4}}V_{1}\end{aligned}
これを(17)式の1行目に代入し
\begin{aligned}n_{1}I_{1}=-\dfrac{n_{2}}{n_{1}Z_{2}}V_{1}-\dfrac{n_{3}}{n_{1}Z_{3}}V_{1} -\dfrac{n_{4}}{n_{1}Z_{4}}V_{1}\end{aligned}
\(I_{1}=\dfrac{V_{o}}{Z_{in}}\)より、上式の左辺に代入すると、求める入力インピーダンス\(Z_{in}\)は
\begin{aligned}Z_{in}=\left \lbrace \left(\dfrac{n_{2}}{n_{1}}\right)^{2}\dfrac{1}{Z_{2}}+\left(\dfrac{n_{3}}{n_{1}}\right)^{2}\dfrac{1}{Z_{3}}+\left(\dfrac{n_{4}}{n_{1}}\right)^{2}\dfrac{1}{Z_{4}}\right \rbrace^{-1}\end{aligned}
参考文献
大学課程 電気回路(1) 第3版 大野 克郎,西 哲生(共著) 第6章