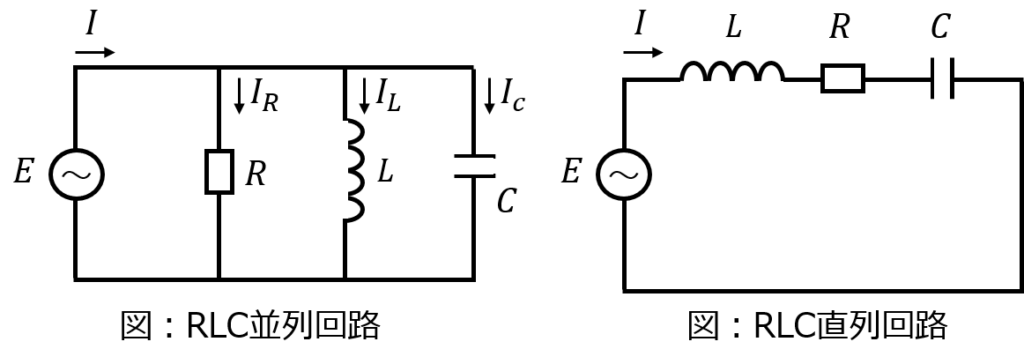
下記のように、RLC並列回路、直列回路を考える。電源電圧\(E=E_{o}\sin(\omega t +\theta)\)を与える時、抵抗R、コイルL、コンデンサCをそれぞれ流れる電流\(I_{R},I_{L},I_{c}\)の瞬時値を求めよ。
瞬時値の求め方
下記2つの方法があります。回路方程式の取り扱いが変わります。
- 微分項、積分項を含む回路方程式に電源電圧を代入し、そのまま微積計算する。
- 微分項、積分項をフェーザ表示で表し、一度計算した後瞬時値に変換する。
交流回路の場合、フェーザ表示で解くことが一般的ですが、それをせずとも1.の方法で微分方程式をそのまま解くことができます。
RLCそれぞれの素子を流れる電流
抵抗の場合は、オームの法則により\(I=V/R\)を考えれば良く、簡単に求まります。
コイルの場合は、誘導起電力の式を電流を左辺に移した式変形をすると求まります。
\begin{aligned}V=L\dfrac{dI_{L}}{dt}\end{aligned}
\begin{aligned}\dfrac{dI_{L}}{dt}&=\dfrac{V}{L} \\ I_{L}&=\dfrac{1}{L}\int V dt\end{aligned}
今回の電気回路では、(2)式のVに電源電圧を代入し、積分することで求まります。
次にコンデンサの場合です。電磁気学でよく用いる\(Q=CV\)の関係式を考えます。\(Q=\int I_{c} dt\)であるので、これをtで微分すると
\begin{aligned}I_{c}=C\dfrac{dV}{dt}\end{aligned}
が得られます。コイルと同様にVには電源電圧を代入することで、実際の値が求まります。
解答例(1) 並列回路
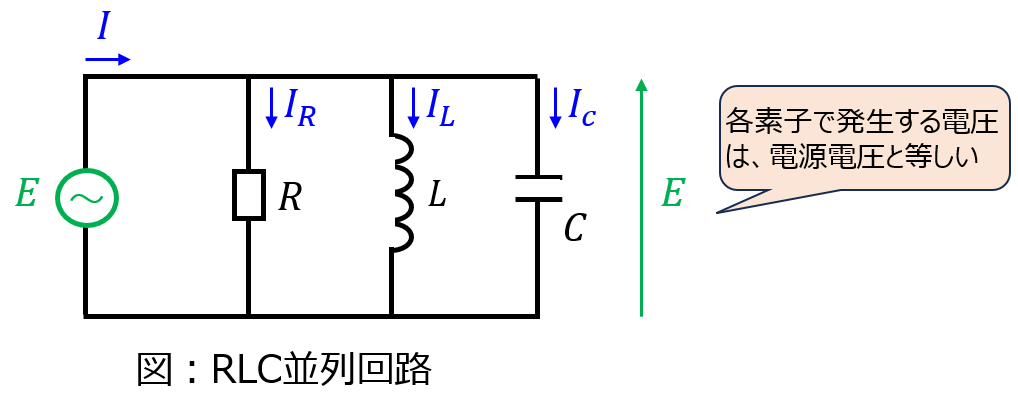
方法1.微分方程式を使用する場合
並列回路の特徴より、\(I_{R},I_{L},I_{c}\)は電源電圧にそれぞれ依存する。
コイルLについて、電源電圧\(E=E_{o}\sin(\omega t +\theta)\)を(2)式(3)式に代入し
\begin{cases}I_{R}=\dfrac{E_{o}}{R}\sin(\omega t + \theta) \\ I_{L}=\dfrac{E_{o}}{L}\int\sin (\omega t+ \theta) \\ I_{c}=CE_{o}\dfrac{d}{dt}\sin (\omega t + \theta)\end{cases}
微分項、積分項を計算すると
\begin{cases}I_{R}=\dfrac{E_{o}}{R}\sin(\omega t + \theta) \\ I_{L}=-\dfrac{E_{o}}{\omega L}\cos (\omega t+ \theta) \\ I_{c}=CE_{o}\omega \cos (\omega t + \theta)\end{cases}
上記が求める電流の瞬時値である。
回路全体に流れる電流値\(I\)は、\(I=I_{R}+I_{L}+I_{c}\)なので
\begin{aligned}I=\dfrac{E_{o}}{R}\sin (\omega t + \theta)+\left(\omega C – \dfrac{1}{\omega L}E_{o}\cos (\omega t + \theta)\right)\end{aligned}
フェーザ表示を用いる方法
コイルL、コンデンサCのインピーダンスから微分項、積分項を排除できる。
- コイルL⇒\(j \omega L\)
- コンデンサC⇒\(\dfrac{1}{j \omega C}\)
上記により、コイルL、コイルCに流れる電流のフェーザ表示は
\begin{cases}I_{L}=\dfrac{E_{o}e^{j \theta}}{j \sqrt{2} \omega L} \\ I_{c}=j \sqrt{2} \omega C e^{j \theta}\end{cases}
で表すことが出来ます。実効値で表すため、電源電圧は、振幅\(E_{o}\)を1/√2倍していることと、
sin(ωt+θ)となっているので、sinを基準に取るとexp項でθ部分を表すことだけ注意しましょう。
基準の位相はsinであるため、虚数jが付いた値はcos波である。実効値に戻すとき、この関係に注意すると、(5)式通りの結果が得られる。
解答例(2) 直列回路

こちらも瞬時値のまま解くことは可能ですが、フェーザ表示で一度答えを出し瞬時値に戻す方法が最も簡単です。
(1)と同じように、電源電圧のフェーザ表示は\(\dfrac{E_{o}}{\sqrt{2}}e^{j\theta}\)
直列回路のため、回路全体のインピーダンス\(Z\)は
\begin{aligned}Z=R+j \omega L+\dfrac{1}{j \omega C}\end{aligned}
よって、回路に流れる電流は、\(I=\dfrac{E_{o}}{\sqrt{2}Z}e^{j\theta}\)なので
\begin{aligned}I=\dfrac{E_{o}e^{j\theta}}{\sqrt{2}\left \lbrace R+ j\left(\omega L-\dfrac{1}{\omega C}\right) \right \rbrace} \end{aligned}
これを瞬時値に戻すには、上式の電源電圧を√2倍、電源電圧と電流の位相差\(\phi\)を
\begin{aligned}\phi=-\tan^{-1}\dfrac{\omega L-\dfrac{1}{\omega C}}{R}\end{aligned}
で表すと、下記のように表現できる。
\begin{aligned}I=\dfrac{E_{o}}{\sqrt{R^{2}+\left(\omega L-\dfrac{1}{\omega C}\right)^{2}}}\sin (\omega t + \theta +\phi)\end{aligned}
虚部と実部を絶対値表記するために、分母でルートを取ることだけ注意しましょう。
最後に
瞬時値の計算は、電通大で問われることがあります。
フェーザ表示での計算ばかりを演習していると、いきなり問われた時に面食らうかもしれません。そんなことが無いように本記事が確認になれば幸いです。