下記の電気回路(1)(2)(3)のベクトル図を作図せよ。
(1)\(E=100[V]\)の交流電源電圧に\(Z=30+j40\)のインピーダンスを接続したときの回路。電源電圧を基準とせよ。(図1)
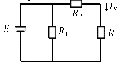
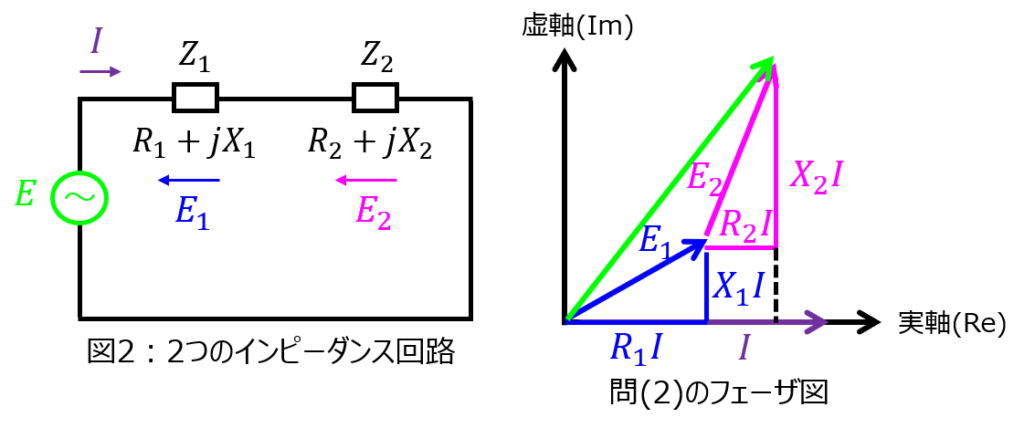
(2)\(Z_{1}=R_{1}+jX_{1},Z_{2}=R_{2}+jX_{2}\)に交流電圧源\(E\)を直列で接続した回路。なお、\(R_{1}>X_{1},R_{2}<X_{2}\)とし、電流\(I\)を基準とせよ。(図2)
(3)抵抗\(R\)、インダクタ\(L\)、キャパシタ\(C\)を直列に接続したRLC直列回路。回路に流れる電流\(I\)を基準とせよ。(図3)

フェーザ図とは
フェーザ表示した電気回路の電圧、電流の関係を複素数平面に図示したものを言います。
瞬時値の概念は無いですが、基準の位相に対する位相差の程度および大きさの程度を直感的に判断できます。
回路の力率を直感的に判断する上で有用な図です。
フェーザ図の作成方法
純粋に、算出した式を複素数平面に図示するだけで良いです。
例えば、下記の電圧、電流がそれぞれフェーザ表示で表せたとしましょう。(それぞれのパラメータに関連性は無いです。)
\begin{aligned}V_{1}=10 \\ V_{2}=10j \\ I=10+10j\end{aligned}
結果は下記の図になります。
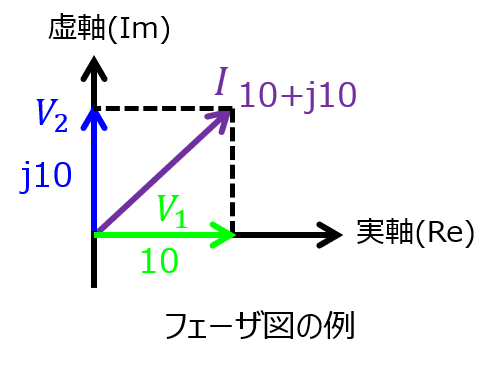
実部と虚部の値にそれぞれ注目し、それぞれのベクトルを合成すれば良いわけですね。
ちなみに、この図の場合、電流\(I\)は電圧\(V_{1}\)に対し45°進んでいます。また、電圧\(V_{2}\)に対し45°遅れています。
作図の際の注意点
回路上の各素子にかかる電圧を合成していくと、電源電圧と等しくなることを念頭に作図しましょう。
例えば、電源電圧Eに対し、抵抗RとコンデンサCを接続した回路を考えます。
\(I=\dfrac{E}{R+\frac{1}{j \omega C}}\)で、分母を有理化すると分子の虚部が正になることから、電源電圧に対して進み電流が生じます。
電流\(I\)を基準としてフェーザ図を作図すると、下記のようになります。
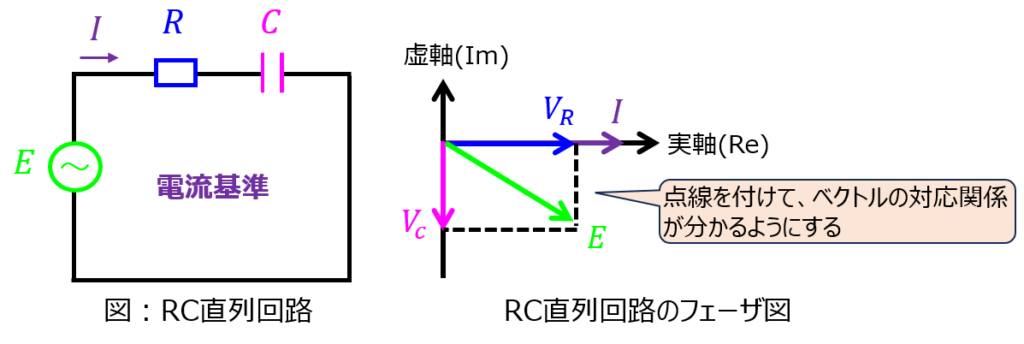
抵抗Rで発生する電圧\(V_{R}=RI=\dfrac{RE}{R+\frac{1}{j \omega C}}\)とコンデンサ\(C\)で発生する電圧\(V_{c}=\dfrac{E}{1+j \omega C R}\)を加算すると、電源電圧\(E\)と等しいことから、ベクトル図としてもそのことが分かるように作図する必要があります。
点線などで対応関係が分かるようにしておくと、試験の採点官からしても親切だと思います。
解答例
(1)のフェーザ図
\(Z=30+j40\)より、インダクタ成分を持つインピーダンスになります。回路に流れる電流は
\begin{aligned}I&=\dfrac{E}{Z} \\ &=\dfrac{100}{30+j40} \\ &=\dfrac{30-j40}{25} \\ &=1.2-j1.6\end{aligned}
\(\phi=-\tan^{-1}\dfrac{1.6}{1.2}=-\tan^{-1}\dfrac{4}{3}\)とする。
\(\sqrt{1.6*1.6+1.2*1.2}=2\)なので
\begin{aligned}I=2 e^{j \phi}\end{aligned}
この関係をベクトル図に表すと、下記のようになる。
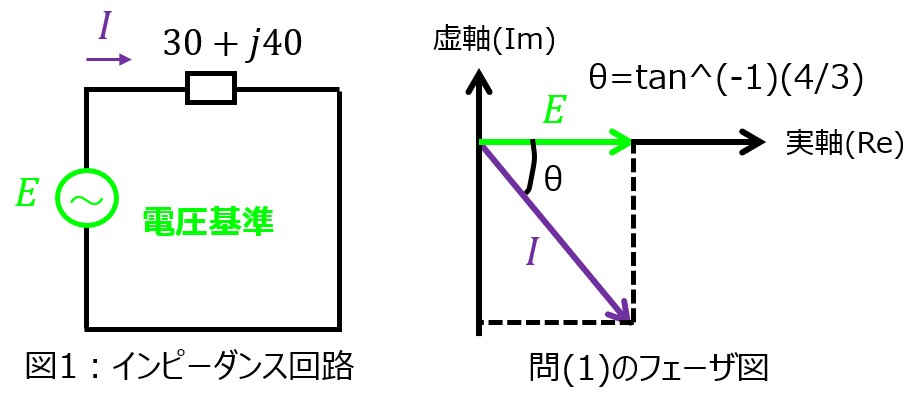
(2)のフェーザ図
素子の数が多くなっただけで、(1)とやることは変わりません。合成するベクトルの数が多くなりますが、結果は電源電圧\(E\)と等しくなることに注目すれば良いです。
回路に流れる電流は
\begin{aligned}I=\dfrac{E}{R_{1}+R_{2}+j(X_{1}+X_{2})}\end{aligned}
\(Z_{1},Z_{2}\)にかかる電圧\(E_{1},E_{2}\)は
\begin{cases}E_{1}=(R_{1}+jX_{1})I \\ E_{2}=(R_{2}+jX_{2})I\end{cases}
\(E_{1}+E_{2}=E\)より、求めるフェーザ図は下記のようになる。
(3)のフェーザ図
同じく、回路を流れる電流\(I\)を求めることを起点にフェーザ図を作成しますが、リアクタンスが(2)と違います。
誘導性のリアクタンス(虚部:正)と容量性のもの(虚部:負)があるため、大小関係により、フェーザ図の内容が変わります。
\begin{aligned}I=\dfrac{E}{R+j\omega L+\frac{1}{j \omega C}}\end{aligned}
抵抗、インダクタ、コンデンサで発生する電圧\(V_{R},V_{L},V_{c}\)は
\begin{cases}V_{R}=\dfrac{RE}{R+j\omega L+\frac{1}{j \omega C}} \\ V_{L}=j \omega L I \\ V_{c}=\dfrac{I}{j \omega C}\end{cases}
ここで、インダクタ成分\(V_{L}\)がキャパシタ成分\(V_{c}\)の大小でフェーザ図の概形が変わる。
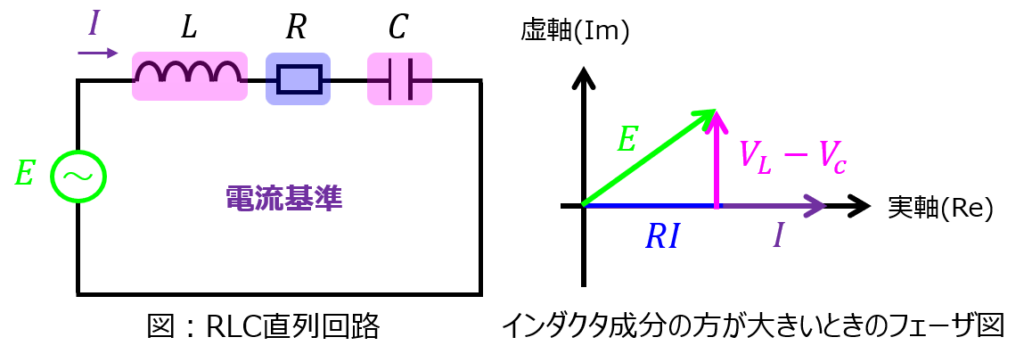
(i)インダクタ成分の方が大きいとき
虚部は正になるため、下記のようなフェーザ図になる。
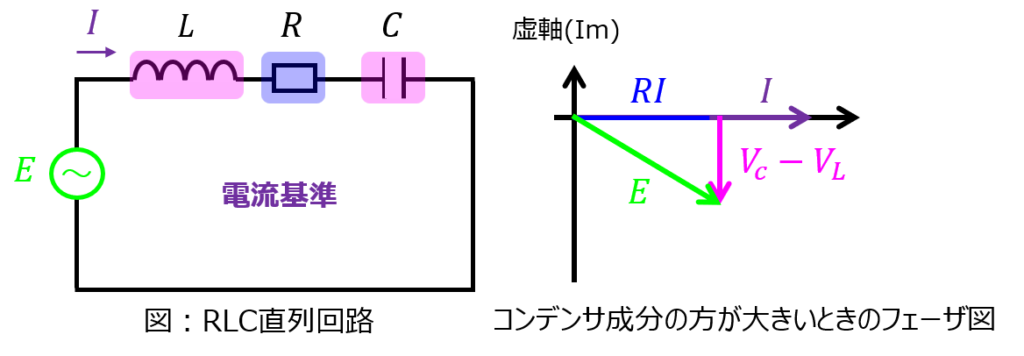
(ii)コンデンサ成分の方が大きいとき
虚部は負になるため、下記のようなフェーザ図になる。
最後に
フェーザ図の作図は、様々な大学の院試で出題されます。
計算した結果に基づいて忠実に作図するだけで、得点できる内容です。是非取りこぼしの無いようにしましょう。