【電磁気学】正対する点電荷の等電位面の計算問題

電磁気学

2025.01.312025.02.01

問題

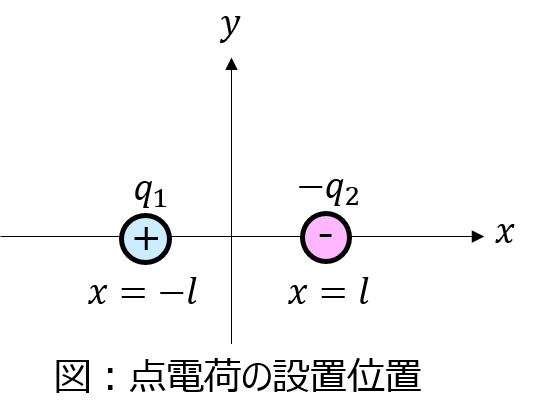
$x = \pm l$ に点電荷 $q_{1}, - q_{2}$ を置く。 $q_{1} > q_{2}$ のとき、下記の問いに答えよ。

(1)電位 $V = 0$ になるx軸上の点を求めよ。
(2)電位 $V = 0$ の等電位線の軌跡を求めよ。

等電位面とは
等電位面の計算方法
解答例
1. (1)電位が0になるx軸上の点
2. (2)等電位面の計算
最後に

等電位面とは

等電位になる線を様々な電位において図示した集合を言います。

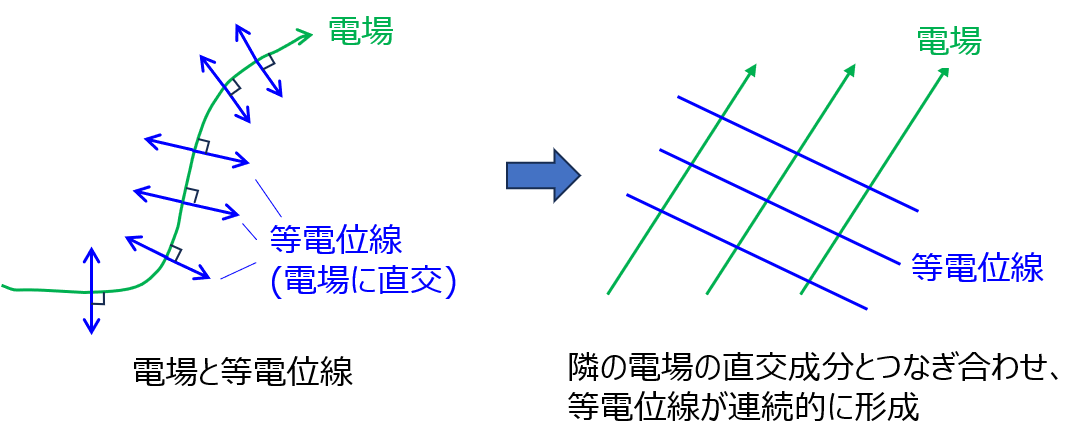
電位は、電場の接線成分の線積分によって増減していきます。ということは、電場に対し垂直になる成分は電位が変化しない=等電位であることが分かります。

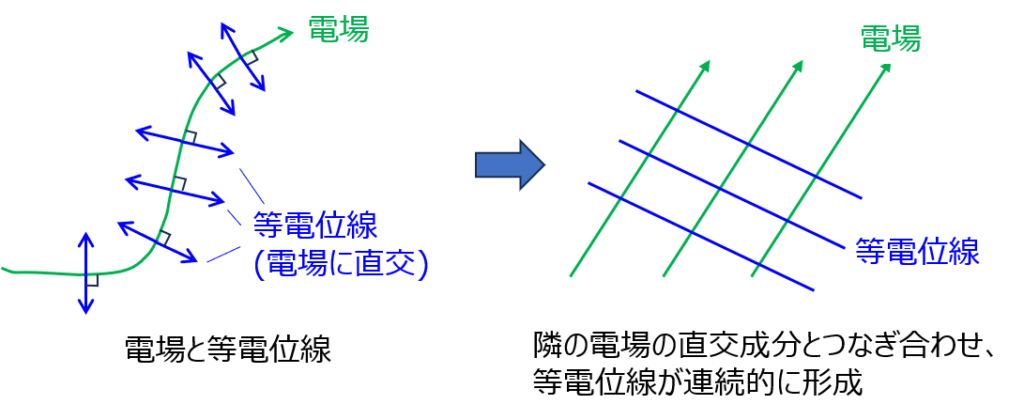
理論上、様々な点において電場の成分が求まれば、それぞれの垂直(内積0)の成分を計算し、隣り合う点とつなぎ合わせることで等電位面が求まります。

電気双極子の記事にて、正対する点電荷から発生する電場、電位分布について考えてきました。本記事では、電位分布をさらに掘り下げ、等電位面について手計算で求めていきます。

等電位面の計算方法

2つの点電荷において、V=0のときに限ってですが、等電位面は円になります。このため、円の方程式

$\begin{matrix} (1) & \begin{array}{r} (x - a)^{2} + (y - b)^{2} = c^{2} \end{array} \end{matrix}$

の形になるように電位 $V$ の式を変形していけば良いです。

電位に関しては、クーロンの式の重ね合わせ

$\begin{matrix} (2) & \begin{array}{r} V = \frac{q_{1}}{4 π ε_{o} r_{1}} + \frac{q_{2}}{4 π ε_{o} r_{2}} \end{array} \end{matrix}$

で考えることができます。本問では、上式に $V = 0$ を代入し、円の方程式を目指して式変形を繰り返すことで解決します。

※V≠0のときは、円とは限らず複雑な方程式になる場合があります。手計算で求めるには厳しく、院試では出題されないはずですが、知識として持っておきましょう。

解答例

(1)電位が0になるx軸上の点

ある点(x,y)における電位は、(2)式より

$\begin{matrix} (3) & \begin{array}{r} V = \frac{q_{1}}{4 π ε_{o} \sqrt{(x + l)^{2} + y^{2}}} - \frac{q_{2}}{4 π ε_{o} \sqrt{(x - l)^{2} + y^{2}}} \end{array} \end{matrix}$

$V = 0, y = 0$ を代入し

$\begin{matrix} (4) & \begin{array}{r} 0 = \frac{q_{1}}{4 π ε_{o} \sqrt{(x + l)^{2}}} - \frac{q_{2}}{4 π ε_{o} \sqrt{(x - l)^{2}}} \end{array} \end{matrix}$

√内は絶対値になりますので、内部の符号に基づき場合分けしていきます。

(i) x>l のとき

√内は全て正になるので

$\begin{matrix} (5) & \begin{aligned} q_{1} x - q_{1} l - q_{2} x - q_{2} l = 0 \\ (q_{1} - q_{2}) x = l (q_{1} + q_{2}) \\ x = \frac{q_{1} + q_{2}}{q_{1} - q_{2}} l \end{aligned} \end{matrix}$

x>lを満たすため、適する。

(ii) -l<x<l のとき

$\begin{matrix} (6) & \begin{aligned} - q_{1} x + q_{1} l - q_{2} x - q_{2} l = 0 \\ (- q_{2} - q_{1}) x = - l (q_{1} - q_{2}) \\ x = \frac{q_{1} - q_{2}}{q_{1} + q_{2}} l \end{aligned} \end{matrix}$

-l<x<lを満たすため、適する。

(iii) x<-l のとき

$\begin{matrix} (7) & \begin{aligned} - q_{1} x + q_{1} l + q_{2} x - q_{2} l = 0 \\ x = \frac{q_{1} + q_{2}}{q_{1} - q_{2}} l \end{aligned} \end{matrix}$

x>0なので、不適。

(1)のまとめ

(i)~(iii)より、求めるx軸上の座標は

$\begin{matrix} (8) & \begin{array}{r} x = \frac{q_{1} + q_{2}}{q_{1} - q_{2}} l, \frac{q_{1} - q_{2}}{q_{1} + q_{2}} l \end{array} \end{matrix}$

(2)等電位面の計算

(3)式にV=0を代入し、円の方程式になるよう変形を進めていく。

$\begin{matrix} (9) & \begin{array}{r} \frac{\sqrt{(x - l)^{2} + y^{2}}}{\sqrt{(x + l)^{2} + y^{2}}} = \frac{q_{2}}{q_{1}} \end{array} \end{matrix}$

$\begin{matrix} (10) & \begin{array}{r} {1 - ({\frac{q_{2}}{q_{1}}}^{2})} x^{2} - 2 l {1 + {(\frac{q_{2}}{q_{1}})}^{2}} x + (l^{2} + y^{2}) {1 - {(\frac{q_{2}}{q_{1}})}^{2}} = 0 \end{array} \end{matrix}$

$\begin{matrix} (11) & \begin{array}{r} x^{2} - 2 l (\frac{q_{1}^{2} + q_{2}^{2}}{q_{1}^{2} - q_{2}^{2}}) + (l^{2} + y^{2}) = 0 \end{array} \end{matrix}$

$\begin{matrix} (12) & \begin{array}{r} {(x - \frac{q_{1}^{2} + q_{2}^{2}}{q_{1}^{2} - q_{2}^{2}})}^{2} + y^{2} = {(\frac{2 q_{1} q_{2}}{q_{1}^{2} - q_{2}^{2}})}^{2} \end{array} \end{matrix}$