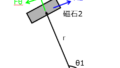
下記のように、コイル面がz軸に垂直になる2つの正方形コイルがある。コイル1は、正方形の中心が原点にあり、一つの辺の長さを\(a\)とする。コイル2は、\(z=d\)の位置に存在し、中心は\(x=y=0\)とする。
(1) 二つのコイルの間の相互インダクタンス\(M\)を求めよ。
なお、辺1から距離\(d\)離れた辺2に対し、辺2の線路に沿ったベクトルポテンシャル\(\boldsymbol{A}\)を-a/2からa/2まで積分した結果を|T(d)|の関数として表す。解答に際しては、この関数を用いて良いこととする。
ノイマンの式とは
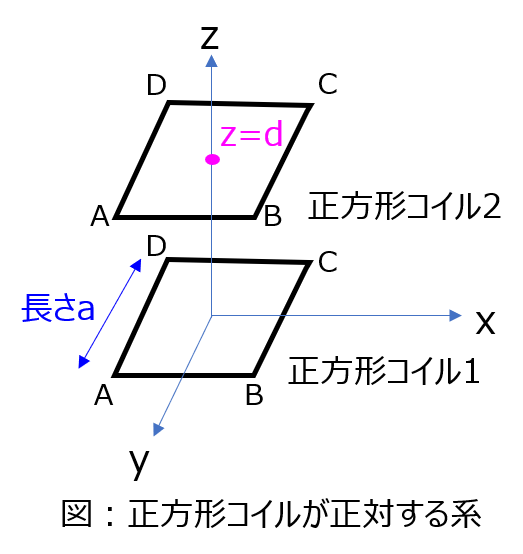
二つのコイルを、形状に沿ってそれぞれ線積分し係数をかけると、その結果が相互インダクタンスになる。という関係を表した式です。
コイル1をかたどる線路を\(C_{1}\)、微小経路を\(d\boldsymbol{s_{1}}\)。コイル2をかたどる線路を\(C_{2}\)、微小経路を\(d\boldsymbol{s_{2}}\)。微小経路間の長さを\(r_{12}\)とすると、下記の式で表されます。
\begin{aligned}M_{12}=\dfrac{\mu_{o}}{4 \pi}\int_{C_{1}}\int_{C_{2}}\dfrac{d\boldsymbol{s_{1}}・d\boldsymbol{s_{2}}}{r_{12}}\end{aligned}
※もし、積分路\(C_{2}\)もコイル1と同様とし、\(C_{1}=C_{2}\)とした際は、自己インダクタンス\(L_{11}\)になります。
ノイマンの式の導出
導出の起点は、磁束と磁束密度の関係式
\begin{aligned}\Phi=\int_{S}\boldsymbol{B}・d\boldsymbol{S}\end{aligned}
です。面積分となっていますが、ベクトルポテンシャルと磁束密度の関係およびストークスの定理を利用し、線積分に帰着させます。
\begin{aligned}\boldsymbol{B}=rot\boldsymbol{A}\end{aligned}
\begin{aligned}\Phi&=\int_{S}\boldsymbol{B}・d\boldsymbol{S} \\ &= \int_{S}rot\boldsymbol{A}・d\boldsymbol{S} \\ &= \int_{c}\boldsymbol{A}・d\boldsymbol{s}\end{aligned}
ベクトルポテンシャル\(\boldsymbol{A}\)は、下記の式で表されます。
\begin{aligned}\boldsymbol{A}=\dfrac{\mu_{o}}{4 \pi } \int_{c} \dfrac{I d\boldsymbol{r}}{\boldsymbol{r}-\boldsymbol{r’}}\end{aligned}
これを(4)式に代入することで、(1)式を導出できます。
ノイマンの式を利用する利点
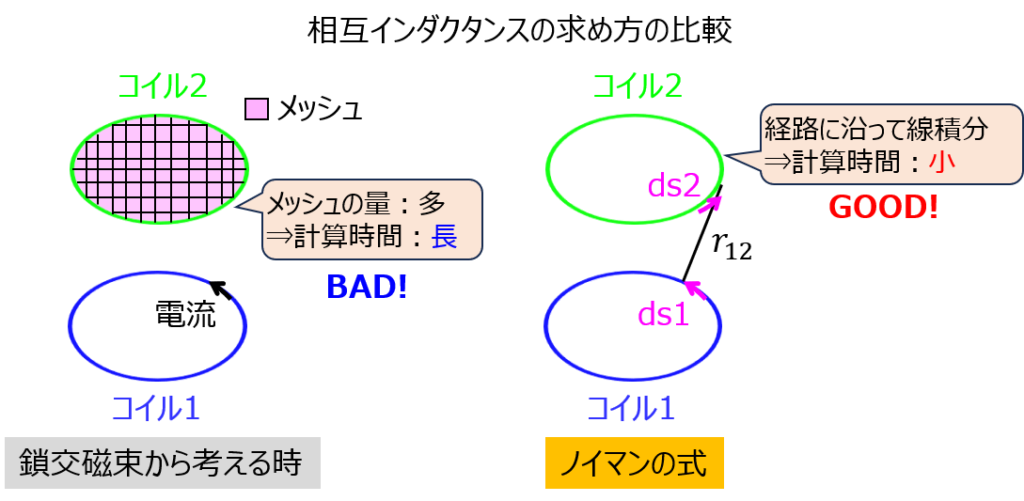
以前の記事でも話したように、一方のコイル1に電流\(I_{1}\)を流し、その時のコイル2の鎖交磁束\(\Phi_{2}\)の量を考えて相互インダクタンスを求める方法もあります。しかし、今回紹介する方法には下記の利点があります。
- 線積分で済むため、計算時間が少ない。
地味に見えて大変な効果です。鎖交磁束を考える時、コイル2の内面をいくつも微小区間分割(メッシュ取り)をする必要があり、メッシュごとに鎖交する磁場の算出⇒面積を乗算する。を繰り返さなければなりません。おまけに、面積を分割する以上、線を分割する行為に対して、どうしても分割数が多くなってしまいます。
(以前の記事では、コイル2が微小円形で、鎖交する磁場が一定である特別な例だったので手計算で求めることができました。しかし、現実にはそんなコイルは殆ど無いです。コイルが大型化するほど、一定磁場と近似できなくなります。)
一方で、ノイマンの式の場合は、磁場を発生させる仮定は不要です。ただ単にコイルの形状に沿って線積分すれば良く、計算回数が大幅に低減できます。
インダクタンスの解釈
ここでもう一度インダクタンスの式を見てみましょう。(再掲)
\begin{aligned}M_{12}=\dfrac{\mu_{o}}{4 \pi}\int_{C_{1}}\int_{C_{2}}\dfrac{d\boldsymbol{s_{1}}・d\boldsymbol{s_{2}}}{r_{12}}\end{aligned}
何か気づいたことはありませんか?特に、電流が流れる導体の材質に関するパラメータが見当たりません。
ここで、インダクタンスに導体の材質の素性は関係ないことが分かります。
実は、インダクタンスは形状で決まります。
(厳密には、コイル内の磁場の鎖交面積の中に磁性体を入れると透磁率\(\mu\)が変わり、インダクタンスも変わりますが、導体の材質には何の関係もありません。)

面積1の円を銅線、アルミニウム、絶縁線、どれを使用して作ろうがインダクタンスの大きさは変わりません。このため、磁束が鎖交したときに発生する誘導起電力も変わりません。
抵抗\(R\)に違いが出るため、同じ誘導起電力でも流れる電流の量が結果的に異なります。
このイメージから、インダクタンスも銅線が一番大きいんじゃないか?と考えてしまいそうですが、実際にそんなことはありません。抵抗とは分けて考えましょう。
導体がn個で構成されている系の全体のインダクタンス
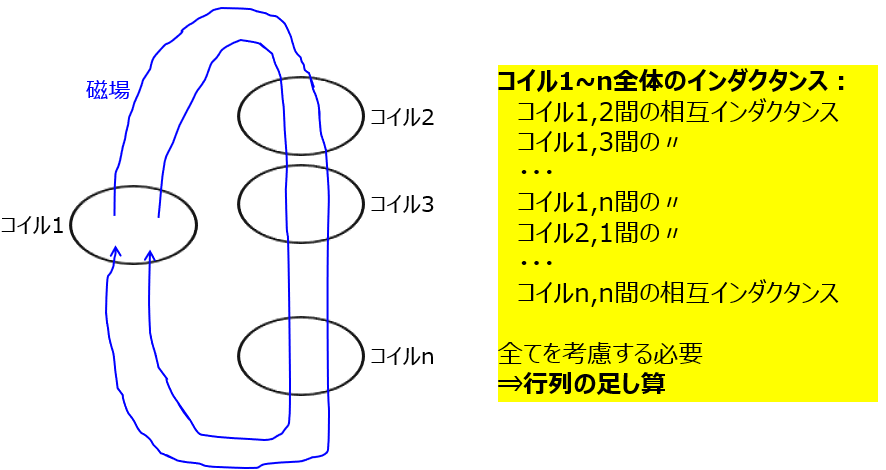
上記のように、コイルが2つだけでなく、n個で構成されている系を考えましょう。この系全体のインダクタンスはどのようにして求まりますか。
結論ですが、下記になります。
導体1の自己インダクタンス、導体2~nの相互インダクタンス
導体2の自己インダクタンス、導体1,3~nの相互インダクタンス
・・・
導体nの自己インダクタンス、導体1~n-1の相互インダクタンス
全て足し算すれば良く、下記で表される。
\begin{aligned}M_{total}=\sum_{i=1}^{n}\sum_{j=1}^{n}M_{ij}\end{aligned}
導体間のインダクタンスの関係は、下記のように行列表示できますが、全部足せば良い。と言うことになります。詳しく見ていきましょう。
\begin{aligned}\begin{pmatrix} M_{11}M_{12} & \ldots M_{1n} \\ M_{21}M_{22} & \ldots M_{2n} \\ \vdots \vdots & \vdots \\ M_{n1} M_{n2} & \ldots M_{nn} \end{pmatrix}\end{aligned}
証明
そもそも全体のインダクタンスとは、“導体1~nを擁するコイルの自己インダクタンス”と捉えることができます。
このため、ノイマンの公式だと、下記の式で表現できます。
\begin{aligned}M_{total}=\dfrac{\mu_{o}}{4 \pi}\int_{C_{1}+C_{2}+\cdots+C_{n}}\int_{C_{1}+C_{2}+\cdots+C_{n}}\dfrac{d\boldsymbol{s_{1}}・d\boldsymbol{s_{2}}}{r_{12}}\end{aligned}
導体1~nの積分路を\(ds_{1},ds_{2}\)二つとも一度は通る。と言うことが分かります。
上式を分解するとどうなるでしょうか?\(C_{1}\)に関して項を分けてみましょう。
\begin{aligned}M_{total}=\dfrac{\mu_{o}}{4 \pi}\int_{C_{1}}\int_{C_{1}+C_{2}+\cdots+C_{n}}\dfrac{d\boldsymbol{s_{1}}・d\boldsymbol{s_{2}}}{r_{12}}+\dfrac{\mu_{o}}{4 \pi}\int_{C_{2}+C_{3}+\cdots+C_{n}}\int_{C_{1}+C_{2}+\cdots+C_{n}}\dfrac{d\boldsymbol{s_{1}}・d\boldsymbol{s_{2}}}{r_{12}}\end{aligned}
右辺の第1項は、インダクタンス成分\(L_{11},M_{12},M_{13},\cdots,M_{1n}\)を表しています。
さらに、\(C_{2}\)に関しても分解すると\(M_{21},L_{22},M_{23},\cdots,M_{2n}\)。\(C_{3}\)から\(C_{n}\)に関しても同じことが言えるため、
結局、冒頭でお見せしたインダクタンス行列の成分を全て足し算しているに過ぎないことが分かりました。
解答例
前章までの説明が本記事のメイントピックだったかもしれません。ただ、冒頭の問題形式で院試問題として実際に出題されたことがあります。しっかり理解していないと完答は厳しかったのではないでしょうか。
内容
コイル1の積分路\(C_{1}\)、コイル2の積分路\(C_{2}\)それぞれは共通してA→B→C→Dの向きとする。コイル1に電流\(I\)が流れているとする。
コイル1のA→Bへの積分路\(C_{AB}\)に対し、コイル2の積分路\(C_{2}=C_{AB}+C_{BC}+C_{CD}+C_{DA}\)を考える。
まず、コイル2の積分路\(C_{AB}\)について、コイル1との積分路の向きが同じで、コイル1の辺ABから長さが\(d\)離れているので
\begin{aligned}T_{AB-AB}=|T(d)|\end{aligned}
次に、コイル2の積分路\(C_{BC},C_{DA}\)に対する相互インダクタンス\(M_{AB-BC},M_{AB-DA}\)を考える。
コイル1との積分路と直交するので
\begin{aligned}d\boldsymbol{s_{1}}・d\boldsymbol{s_{2}}=ds_{1}ds_{2}\cos \frac{\pi}{2}=0\end{aligned}
これを(6)式に代入すると
\begin{aligned}T_{AB-BC}=T_{AB-DA}=0\end{aligned}
最後に、コイル2との積分路\(C_{CD}\)について、コイル1と積分路の向きが逆で、距離が\(\sqrt{a^{2}+d^{2}}\)離れているので
\begin{aligned}T_{AB-CD}=-|T(\sqrt{a^{2}+d^{2}})|\end{aligned}
よって、コイル1の辺ABに対するコイル2の相互インダクタンス\(M_{AB2}\)は、ベクトルポテンシャルの線積分の結果から電流\(I\)を除算することに注意して
\begin{aligned}M_{AB2}&=\dfrac{T_{AB-AB}+T_{AB-BC}+T_{AB-DA}+T_{AB-CD}}{I} \\ &=\dfrac{|T(d)|-|T(\sqrt{a^{2}+d^{2}})|}{I}\end{aligned}
コイル1の辺BC,CD,DAに関しても同じ結果になるので、求める相互インダクタンスは上式の結果を4倍すればよく
\begin{aligned}M=\dfrac{4|T(d)|-4|T(\sqrt{a^{2}+d^{2}})|}{I}\end{aligned}
最後に
本問は、コイルを理解するために重要な知識が詰まっています。社会に出てからもインダクタンスの概念はよく出てきます。問題は解けなくても、“形状で決まる”ところだけは、是非とも覚えていただきたいです。