重ね合わせの理の説明と問題を用いた解説

問題

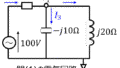
下記の回路に流れる電流 $I$ を、重ね合わせの理を用いて答えよ。

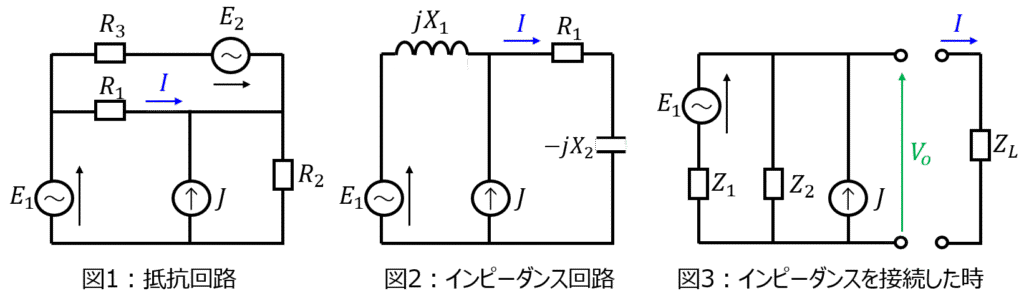
(1)交流電圧源 $E_{1}, E_{2}$ 、定電流源 $J$ を接続した抵抗回路。
(2)交流電圧源 $E_{1}$ と定電流源 $J$ を接続したインピーダンス回路
(3)交流電圧源 $E_{1}$ と定電流源 $J$ を接続したインピーダンス回路に $Z_{L}$ を接続したときの電流

重ね合わせの理とは

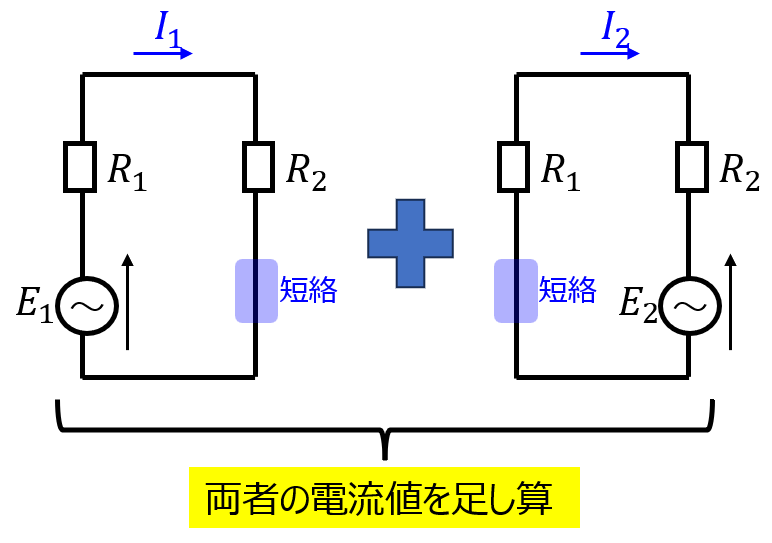
複数の電圧源、電流源から発生する電流は、一つの電源を残し、他は全て殺した状態から発生する電流を個々に足し合わせた結果に等しいことを言います。

例

下記の回路を考えます。

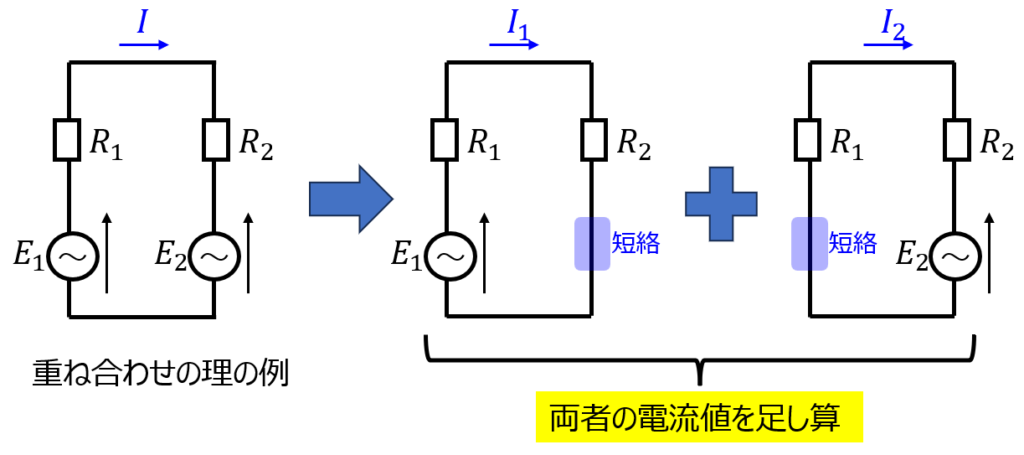
電圧源 $E_{1}, E_{2}$ から抵抗 $R_{3}$ へ流れる電流は

電圧源 $E_{1}$ が存在し、電圧源 $E_{2}$ を短絡した回路
電圧源 $E_{2}$ が存在し、電圧源 $E_{1}$ を短絡した回路

の個々の結果1.2.の足し合わせで求められます。

1.のとき、抵抗部分に流れる電流は $I_{1} = \frac{E_{1}}{R_{1} + R_{2}}$
2.のとき、抵抗部分に流れる電流は $I_{2} = - \frac{E_{2}}{R_{1} + R_{2}}$

だから、結果は $I = I_{1} + I_{2}$ より

$\begin{matrix} (1) & \begin{array}{r} I = \frac{E_{1}}{R_{1} + R_{2}} - \frac{E_{2}}{R_{1} + R_{2}} \end{array} \end{matrix}$

になります。電流源の場合でも、個々に考えることで求まります。

注目した電源以外の取り扱い

電圧源を無効化するとき：該当の電圧源を短絡する
電流源を無効化するとき：該当の電流源を開放する

電圧源は定電圧 $E$ を出し続ける素子です。ですので、無効化するときは電圧を0⇒短絡すれば良いです。

また、電流源は定電流 $I$ を出し続けるため、 $I = 0$ ⇒開放すれば良いわけですね。

重ね合わせの理が成立する理由

回路上に存在する素子(電圧源、電流源、抵抗、コンデンサ、インダクタンス)が線形素子であるためです。

キルヒホッフの法則は線形方程式であるため、別々で考えた結果を足し合わせても最終的な結果に変わりありません。上記の素子のみが存在する場合に限り有効と言うわけですね。

ダイオードなど、非線形素子が回路上に存在するときは使用できませんのでご注意ください。

解答例

(1)抵抗回路

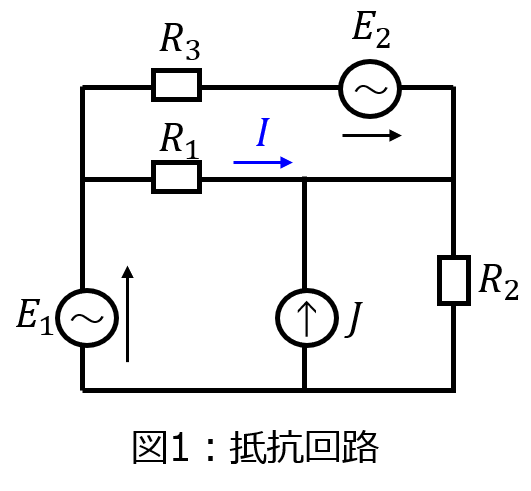
前節と同じように、電圧源 $E_{1}, E_{2}$ 、電流源 $J$ を順に考えていきます。

$E_{1}$ のみ考えるとき

下記の電気回路となる。

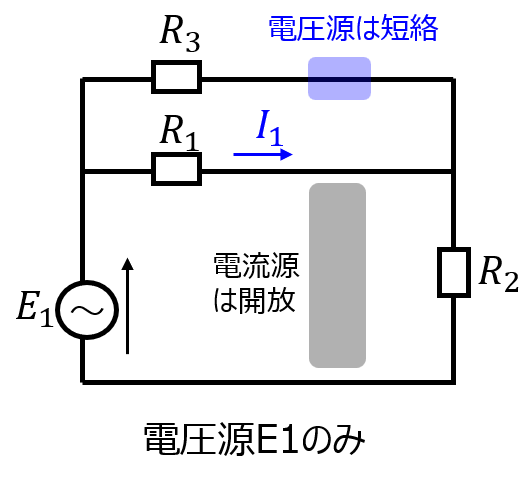
抵抗 $R_{1}$ に流れる電流 $I_{1}$ は、分圧の法則により

$\begin{matrix} (2) & \begin{aligned} I_{1} & = \frac{E_{1}}{R_{2} + \frac{R_{1} R_{3}}{R_{1} + R_{3}}} \frac{R_{3}}{R_{1} + R_{3}} \\ = \frac{R_{3} E_{1}}{R_{1} R_{2} + R_{2} R_{3} + R_{1} R_{3}} \end{aligned} \end{matrix}$

$E_{2}$ のみ考えるとき

下記の電気回路となる。

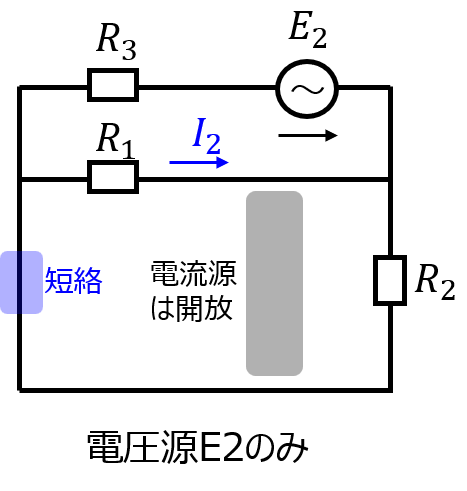
同じく、抵抗 $R_{1}$ に流れる電流 $I_{2}$ は、 $R_{1}, R_{2}$ の並列回路より

$\begin{matrix} (3) & \begin{aligned} I_{2} & = - \frac{E_{2}}{R_{3} + \frac{R_{1} R_{2}}{R_{1} + R_{2}}} \frac{R_{2}}{R_{1} + R_{2}} \\ = - \frac{R_{2} E_{2}}{R_{1} R_{2} + R_{2} R_{3} + R_{1} R_{3}} \end{aligned} \end{matrix}$

$J$ のみ考えるとき

抵抗 $R_{1}$ と抵抗 $R_{2}, R_{3}$ の並列回路となるので

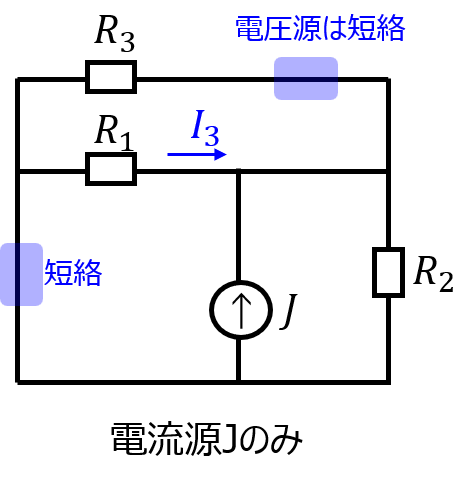
$\begin{matrix} (4) & \begin{aligned} I_{3} & = - \frac{\frac{R_{2} R_{3}}{R_{2} + R_{3}}}{R_{1} + \frac{R_{2} R_{3}}{R_{2} + R_{3}}} J \\ = - \frac{R_{2} R_{3}}{R_{1} R_{2} + R_{2} R_{3} + R_{1} R_{3}} J \end{aligned} \end{matrix}$

抵抗 $R_{3}$ に流れる電流

$I_{1} + I_{2} + I_{3}$ を計算すれば良く

$\begin{matrix} (5) & \begin{array}{r} I = \frac{R_{3} E_{1} - R_{2} E_{2} - R_{2} R_{3} J}{R_{1} R_{2} + R_{2} R_{3} + R_{1} R_{3}} \end{array} \end{matrix}$

(2)インピーダンス回路

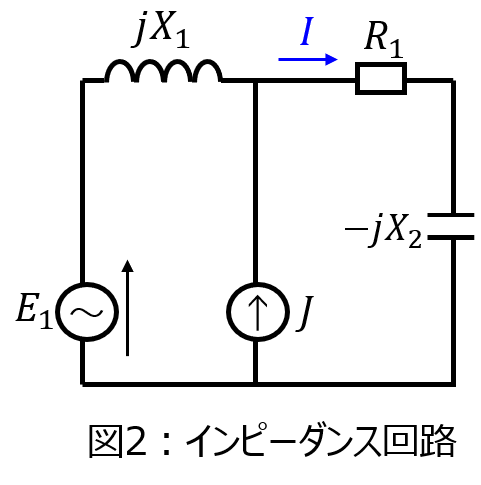
リアクタンスは存在しますが、フェーザ表示として計算をすれば良いです。

電圧源に注目するとき

下記のように、直列の回路となる。

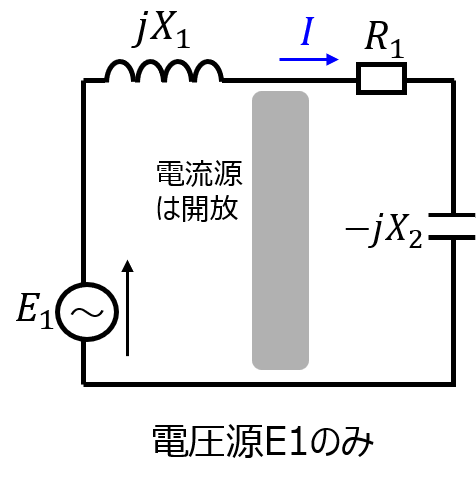
流れる電流 $I_{1}$ は

$\begin{matrix} (6) & \begin{array}{r} I_{1} = \frac{E}{R_{1} + j (X_{1} - j X_{2})} \end{array} \end{matrix}$

電流源に注目するとき

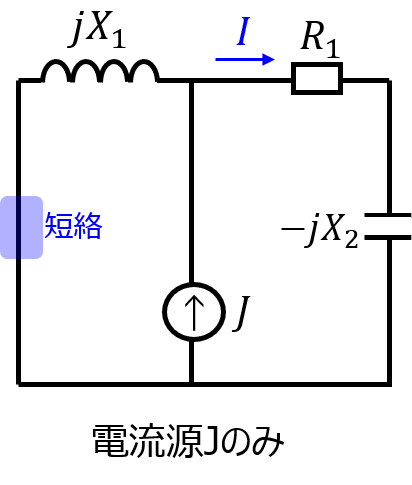
$X_{1}$ と $R_{1}, X_{1}$ の並列回路となる。

$\begin{matrix} (7) & \begin{array}{r} I_{2} = \frac{j X_{1} I_{o}}{R + j (X_{1} - X_{2})} \end{array} \end{matrix}$

注意点

電流源Jは交流である前提です。本問の電圧源Jはフェーザ表示である前提で、時間表示に直すと√2Jsinωtです。このため、リアクタンスも計算に考慮する必要があります。

電流源が時間領域で見ても一定値の場合は、十分に時間が経つとコンデンサに電流が流れなくなります。(開放)
また、コイルに電圧が立たなくなり、短絡扱いになります。

是非区別してできるようにしましょう。

抵抗に流れる電流

$I_{1} + I_{2}$ を計算すれば良く

$\begin{matrix} (8) & \begin{array}{r} I = \frac{E}{R_{1} + j (X_{1} - j X_{2})} + \frac{j X_{1} I_{o}}{R + j (X_{1} - X_{2})} \end{array} \end{matrix}$

(3)インピーダンスの接続時

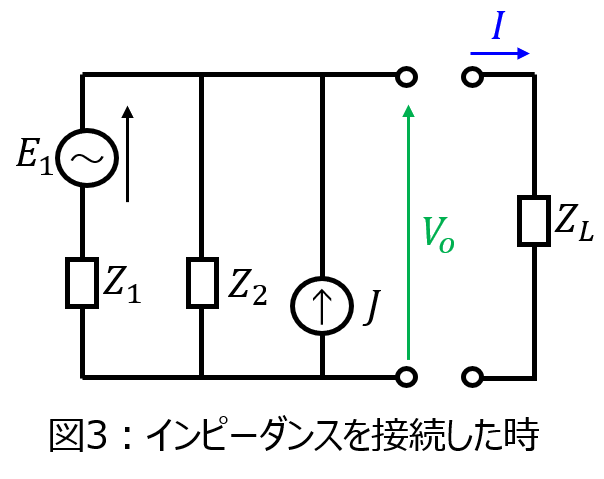
これは、テブナンの定理の考え方を用います。

インピーダンス$Z_{L]$を接続していないときの出力端の電圧 $V_{o}$ を重ね合わせの理を用いて算出。

出力端から見たインピーダンス $Z_{o}$ を計算し、そこに $Z_{L}$ を接続することで、求める電流値

$\begin{matrix} (9) & \begin{array}{r} I = \frac{V_{o}}{Z_{o} + Z_{L}} \end{array} \end{matrix}$

を求めます。

電圧源のみを残すとき

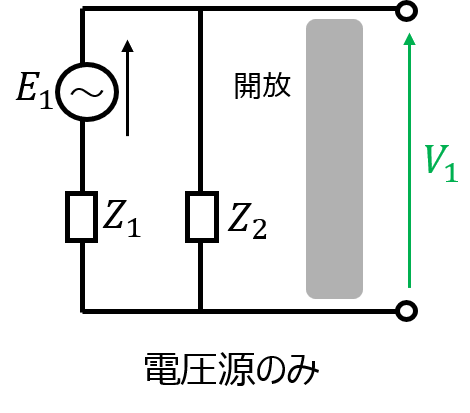
このとき、出力端の電圧 $V_{1}$ は

$\begin{matrix} (10) & \begin{array}{r} V_{1} = \frac{Z_{2}}{Z_{1} + Z_{2}} E \end{array} \end{matrix}$

電流源のみを残すとき

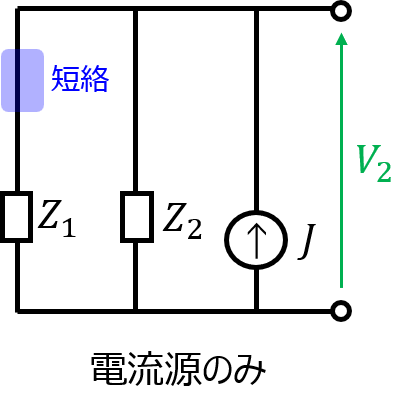
出力端の電圧 $V_{2}$ は

$\begin{matrix} (11) & \begin{array}{r} V_{2} = \frac{Z_{1} Z_{2}}{Z_{1} + Z_{2}} J \end{array} \end{matrix}$

出力端の電圧

前節より、 $V_{1}, V_{2}$ を足せば良い。

$\begin{matrix} (12) & \begin{array}{r} V_{o} = \frac{Z_{2} E + Z_{1} Z_{2} J}{Z_{1} + Z_{2}} \end{array} \end{matrix}$

また、出力端から見たインピーダンス $Z_{o}$ は

$\begin{matrix} (13) & \begin{array}{r} Z_{o} = \frac{Z_{1} Z_{2}}{Z_{1} + Z_{2}} \end{array} \end{matrix}$

$Z_{L}$ に流れる電流

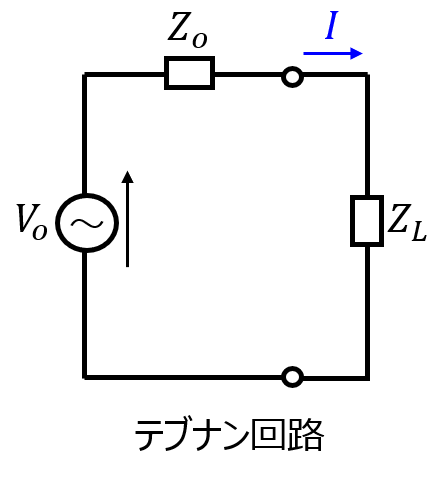
テブナンの定理より、

$\begin{matrix} (14) & \begin{aligned} I & = \frac{V_{o}}{Z_{o} Z_{L}} \\ = \frac{Z_{2} E + Z_{1} Z_{2} J}{Z_{1} Z_{2} + Z_{L} (Z_{1} + Z_{2})} \end{aligned} \end{matrix}$

最後に

重ね合わせの理は、どこの大学の院試でも毎年のように出題される内容です。

電気系の学生/エンジニアであるならば、本記事に記載した問題は完答必須です。今は勉強段階でも、必ずできるようにしましょう。